Let $\Gamma $ be a discrete group and let 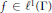$f\,\in \,{{l}^{1}}(\Gamma )$ . We observe that if the natural convolution operator 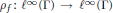$\rho f\,:\,{{l}^{\infty }}(\Gamma )\,\to \,{{l}^{\infty }}(\Gamma )$ is injective, then 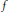$f$ is invertible in 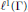${{l}^{1}}(\Gamma )$ . Our proof simplifies and generalizes calculations in a preprint of Deninger and Schmidt by appealing to the direct finiteness of the algebra 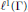${{l}^{1}}(\Gamma )$ .

We give simple examples to show that in general one cannot replace 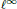${{l}^{\infty }}$ with 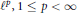${{l}^{p}},\,1\,\le \,p\,<\,\infty $ , nor with 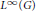${{L}^{\infty }}(G)$ for nondiscrete $G$ . Finally, we consider the problem of extending the main result to the case of weighted convolution operators on $\Gamma $ , and give some partial results.