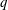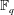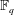Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dartyge, Cécile
Mérai, László
and
Winterhof, Arne
2021.
On the distribution of the Rudin-Shapiro function for finite fields.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 12,
p.
5013.
Mérai, László
and
Winterhof, Arne
2022.
Pseudorandom sequences derived from automatic sequences.
Cryptography and Communications,
Vol. 14,
Issue. 4,
p.
783.
Bary-Soroker, Lior
Koukoulopoulos, Dimitris
and
Kozma, Gady
2023.
Irreducibility of random polynomials: general measures.
Inventiones mathematicae,
Vol. 233,
Issue. 3,
p.
1041.
Cheng, Kaimin
2025.
Counting irreducible polynomials with restricted coefficients.
Finite Fields and Their Applications,
Vol. 108,
Issue. ,
p.
102691.
Bary-Soroker, Lior
and
Shmueli, Roy
2026.
Irreducibility of polynomials with square coefficients over finite fields.
Finite Fields and Their Applications,
Vol. 109,
Issue. ,
p.
102714.