No CrossRef data available.
Article contents
Kolmogorov, Linear and Pseudo-Dimensional Widths of Classes of s-Monotone Functions in 𝕃p , 0 < p < 1
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 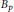 ${{B}_{p}}$ be the unit ball in
${{B}_{p}}$ be the unit ball in 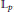 ${{\mathbb{L}}_{p}}$ ,
${{\mathbb{L}}_{p}}$ , 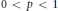 $0\,<\,p\,<\,1$ , and let
$0\,<\,p\,<\,1$ , and let 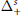 $\Delta _{+}^{s}$ ,
$\Delta _{+}^{s}$ , 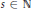 $s\,\in \,\mathbb{N}$ , be the set of all
$s\,\in \,\mathbb{N}$ , be the set of all  $s$ -monotone functions on a finite interval
$s$ -monotone functions on a finite interval  $I$ , i.e.,
$I$ , i.e., 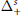 $\Delta _{+}^{s}$ consists of all functions
$\Delta _{+}^{s}$ consists of all functions 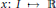 $x\,:\,I\,\mapsto \,\mathbb{R}$ such that the divided differences
$x\,:\,I\,\mapsto \,\mathbb{R}$ such that the divided differences 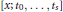 $[x;\,{{t}_{0}},\,...\,,\,{{t}_{s}}]$ of order
$[x;\,{{t}_{0}},\,...\,,\,{{t}_{s}}]$ of order  $s$ are nonnegative for all choices of
$s$ are nonnegative for all choices of 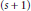 $\left( s\,+\,1 \right)$ distinct points
$\left( s\,+\,1 \right)$ distinct points  ${{t}_{0}},\,.\,.\,.\,,{{t}_{s}}\,\in \,I.$ For the classes
${{t}_{0}},\,.\,.\,.\,,{{t}_{s}}\,\in \,I.$ For the classes 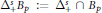 $\Delta _{+}^{s}{{B}_{P}}\,:=\,\Delta _{+}^{s}\,\cap \,{{B}_{P}},$ we obtain exact orders of Kolmogorov, linear and pseudo-dimensional widths in the spaces
$\Delta _{+}^{s}{{B}_{P}}\,:=\,\Delta _{+}^{s}\,\cap \,{{B}_{P}},$ we obtain exact orders of Kolmogorov, linear and pseudo-dimensional widths in the spaces 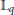 ${{\mathbb{L}}_{q}},$
${{\mathbb{L}}_{q}},$ 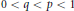 $0\,<\,q\,<\,p\,<\,1$ :
$0\,<\,q\,<\,p\,<\,1$ :
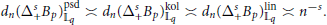 $${{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{psd}}\asymp {{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{kol}}\asymp {{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{lin}}\asymp {{n}^{-s}}.$$
$${{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{psd}}\asymp {{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{kol}}\asymp {{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{lin}}\asymp {{n}^{-s}}.$$
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2008

