Article contents
Linear Operators Preserving Generalized Numerical Ranges and Radii on Certain Triangular Algebras of Matrices
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 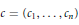 $c\,=\,\left( {{c}_{1}},\ldots ,{{c}_{n}} \right)$ be such that
$c\,=\,\left( {{c}_{1}},\ldots ,{{c}_{n}} \right)$ be such that 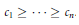 ${{c}_{1}}\,\ge \,\cdots \,\ge \,{{c}_{n}}$ . The
${{c}_{1}}\,\ge \,\cdots \,\ge \,{{c}_{n}}$ . The 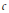 $c$ -numerical range of an
$c$ -numerical range of an 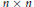 $n\,\times \,n$ matrix
$n\,\times \,n$ matrix 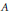 $A$ is defined by
$A$ is defined by
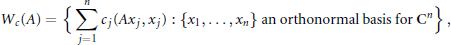 $${{W}_{c}}\left( A \right)\,=\,\left\{ \sum\limits_{j=1}^{n}{{{c}_{j}}\left( A{{x}_{j}},\,{{x}_{j}} \right)\,:\,\left\{ {{x}_{1}},\ldots ,{{x}_{n}} \right\}\,\text{an}\,\text{orthonormal basis for }{{\mathbf{C}}^{n}}} \right\}\,,$$
$${{W}_{c}}\left( A \right)\,=\,\left\{ \sum\limits_{j=1}^{n}{{{c}_{j}}\left( A{{x}_{j}},\,{{x}_{j}} \right)\,:\,\left\{ {{x}_{1}},\ldots ,{{x}_{n}} \right\}\,\text{an}\,\text{orthonormal basis for }{{\mathbf{C}}^{n}}} \right\}\,,$$
and the 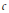 $c$ -numerical radius of
$c$ -numerical radius of 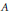 $A$ is defined by
$A$ is defined by 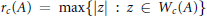 ${{r}_{c}}\left( A \right)\,=\,\max \left\{ \left| z \right|\,:\,z\,\in \,{{W}_{c}}\left( A \right) \right\}$ . We determine the structure of those linear operators
${{r}_{c}}\left( A \right)\,=\,\max \left\{ \left| z \right|\,:\,z\,\in \,{{W}_{c}}\left( A \right) \right\}$ . We determine the structure of those linear operators 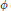 $\phi$ on algebras of block triangular matrices, satisfying
$\phi$ on algebras of block triangular matrices, satisfying
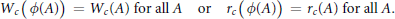 $${{W}_{c}}\left( \phi \left( A \right) \right)={{W}_{c}}\left( A \right)\text{for}\,\,\text{all}\,\,A\,\text{or}\,\,{{r}_{c}}\left( \phi \left( A \right) \right)={{r}_{c}}\left( A \right)\text{for}\,\,\text{all}\,A.$$
$${{W}_{c}}\left( \phi \left( A \right) \right)={{W}_{c}}\left( A \right)\text{for}\,\,\text{all}\,\,A\,\text{or}\,\,{{r}_{c}}\left( \phi \left( A \right) \right)={{r}_{c}}\left( A \right)\text{for}\,\,\text{all}\,A.$$
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2001
References
- 7
- Cited by

