Hostname: page-component-cb9f654ff-hn9fh Total loading time: 0 Render date: 2025-08-19T23:36:11.431Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Operators Preserving Similarity Classes and Related Results

Published online by Cambridge University Press:  20 November 2018

Chi-Kwong Li  and
Stephen Pierce
Chi-Kwong Li
Affiliation:
Department of Mathematics, The College of William and Mary Williamsburg, Virginia 23187 U.S.A.
Stephen Pierce
Affiliation:
Department of Mathematical Sciences, San Diego State University, San Diego, California 92182, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

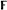Let Mn be the algebra of n × n matrices over an algebraically closed field of characteristic zero. For A ∊ Mn , denote by 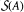the collection of all matrices in Mn that are similar to A. In this paper we characterize those invertible linear operators ϕ on Mn that satisfy 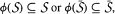, where 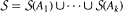for some given A1,..., Ak ∊ Mn and 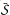denotes the (Zariski) closure of S. Our theorem covers a result of Howard on linear operators mapping the set of matrices annihilated by a given polynomial into itself, and extends a result of Chan and Lim on linear operators commuting with the function f(x) = xk for a given positive integer k ≥ 2. The possibility of weakening the invertibility assumption in our theorem is considered, a partial answer to a conjecture of Howard is given, and some extensions of our result to arbitrary fields are discussed.

Keywords

15A42

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 37 , Issue 3 , 01 September 1994 , pp. 374 - 383
Copyright
Copyright © Canadian Mathematical Society 1994

References

[BeP] Beasley, L. B. and Pullman, N. B., Linear operators preserving idempotent matrices over fields, Linear Algebra Appl. 146( 1991 ), 7–20.Google Scholar
[BPW] Botta, E. P., Pierce, S. and Watkins, W., Linear transformations that preserve the nilpotent matrices, Pacific J. Math. 104(1983), 39–46.Google Scholar
[BrS] Bresar, M. and Semrl, P., Linear transformations preserving potent matrices, Proc. Amer. Math. Soc, to appear.Google Scholar
[CL1] Chan, G. H. and Lim, M. H., Linear preservers on powers of matrices, Linear Algebra Appl. 162- 164(1992), 615–626.Google Scholar
[CL2] Chan, G. H. and Lim, M. H., Linear transformations on symmetric matrices II, Linear and Multilinear Algebra 32(1992), 319–326.Google Scholar
[Di] Dixon, J., Rigid embeddings of simple groups in the general linear group, Canad. J. Math. 29(1977), 384– 391.Google Scholar
[H] Howard, R., Linear maps that preserve matrices annihilated by a polynomial, Linear Algebra Appl. 30 (1980), 167–176.Google Scholar
[Hum] Humphreys, J. E., Linear Algebraic Groups, Graduate Texts in Math. 21, Springer, New York, 1975.Google Scholar
[JS] Johnson, C. R. and Shapiro, H., Mathematical aspects of the relative gain array [A • A-1 ]*, SIAM J. Algebra Discrete Math. 7(1986), 627–644.Google Scholar
[W] Watkins, W., Linear transformations that preserve a similarity class of matrices, Linear and Multilinear Algebra 11(1982), 19–22.Google Scholar