Let $A$ be a subgroup of a finite group 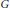$G$ and 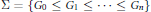$\sum \,=\,\{{{G}_{0}}\,\le \,{{G}_{1}}\,\le \,.\,.\,.\,\le \,{{G}_{n}}\}$ some subgroup series of 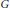$G$ . Suppose that for each pair 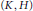$\left( K,\,H \right)$ such that 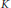$K$ is a maximal subgroup of 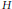$H$ and 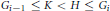${{G}_{i-1}}\,\le \,K\,<\,H\,\le \,{{G}_{i}}$ , for some i, either 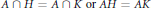$A\,\cap \,H\,=\,A\,\cap \,K\,\text{or}\,\text{AH}\,\text{=}\,\text{AK}$ . Then $A$ is said to be 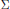$\sum$ -embedded in 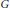$G$ . And $A$ is said to be 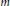$m$ -embedded in 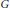$G$ if 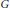$G$ has a subnormal subgroup 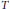$T$ and 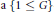$a\,\{1\,\le \,G\}$ -embedded subgroup 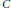$C$ in 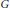$G$ such that 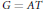$G\,=\,AT$ and 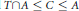$T\cap A\,\le \,C\,\le \,A$ . In this article, some sufficient conditions for a finite group 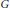$G$ to be 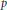$p$ -nilpotent are given whenever all subgroups with order 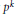${{p}^{k}}$ of a Sylow 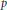$p$ -subgroup of 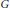$G$ are 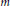$m$ -embedded for a given positive integer $k$ .