Abstract. A subset 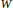$W$ of the vertex set of a graph 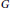$G$ is called a resolving set of 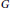$G$ if for every pair of distinct vertices 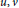$u,\,v$ , of 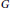$G$ , there is 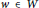$w\,\in \,W$ such that the distance of $w$ and 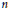$u$ is different from the distance of $w$ and $v$ . The cardinality of a smallest resolving set is called the metric dimension of 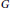$G$ , denoted by 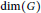$\dim\left( G \right)$ . The circulant graph 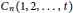${{C}_{n}}\left( 1,\,2,\,.\,.\,.\,,\,t \right)$ consists of the vertices 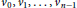${{v}_{0}},\,{{v}_{1\,}},\,.\,.\,.\,,{{v}_{n\,-\,1}}$ and the edges 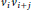${{v}_{i}}{{v}_{i\,+\,j}}$ , where 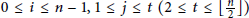$0\,\le \,i\,\le \,n\,-\,1,1\,\le \,j\,\le \,t\,\left( 2\,\le \,t\,\le \,\left\lfloor \frac{n}{2} \right\rfloor\right)$ , the indices are taken modulo $n$ . Grigorious, Manuel, Miller, Rajan, and Stephen proved that 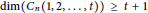$\dim\left( {{C}_{n}}\left( 1,\,2,\,.\,.\,.\,,\,t \right) \right)\,\ge \,t\,+\,1$ for 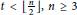$t\,<\,\left\lfloor \frac{n}{2} \right\rfloor ,\,n\,\ge \,3$ , and they presented a conjecture saying that 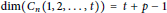$\dim\left( {{C}_{n}}\left( 1,\,2,\,.\,.\,.\,,\,t \right) \right)\,=\,t\,+\,p\,-\,1$ for 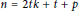$n\,=\,2tk\,+\,t\,+\,p$ , where 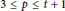$3\,\le \,p\,\le \,t\,+\,1$ . We disprove both statements. We show that if 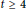$t\,\ge \,4$ is even, there exists an infinite set of values of $n$ such that 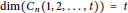$\dim\left( {{C}_{n}}\left( 1,\,2,\,.\,.\,.\,,t \right) \right)\,=\,t$ . We also prove that 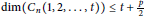$\dim\left( {{C}_{n}}\left( 1,\,2,\,.\,.\,.\,,\,t \right) \right)\,\le \,t\,+\,\frac{p}{2}$ for 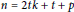$n\,=\,2tk\,+\,t\,+\,p$ , where $t$ and 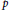$p$ are even, 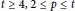$t\,\ge \,4,\,2\,\le \,p\,\le \,t$ , and 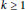$k\,\ge \,1$ .