Article contents
The Milnor–Stasheff Filtration on Spaces and Generalized Cyclic Maps
Published online by Cambridge University Press: 20 November 2018
Abstract
The concept of 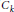 ${{C}_{k}}$ -spaces is introduced, situated at an intermediate stage between
${{C}_{k}}$ -spaces is introduced, situated at an intermediate stage between 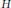 $H$ -spaces and
$H$ -spaces and  $T$ -spaces. The
$T$ -spaces. The 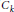 ${{C}_{k}}$ -space corresponds to the
${{C}_{k}}$ -space corresponds to the  $k$ -th Milnor–Stasheff filtration on spaces. It is proved that a space
$k$ -th Milnor–Stasheff filtration on spaces. It is proved that a space 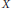 $X$ is a
$X$ is a 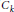 ${{C}_{k}}$ -space if and only if the Gottlieb set
${{C}_{k}}$ -space if and only if the Gottlieb set 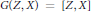 $G(Z,\,X)\,=\,[Z,\,X]$ for any space
$G(Z,\,X)\,=\,[Z,\,X]$ for any space 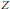 $Z$ with cat
$Z$ with cat 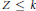 $Z\,\le \,k$ , which generalizes the fact that
$Z\,\le \,k$ , which generalizes the fact that 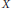 $X$ is a
$X$ is a  $T$ -space if and only if
$T$ -space if and only if 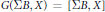 $G(\sum B,\,X)\,=\,[\sum B,\,X]$ for any space
$G(\sum B,\,X)\,=\,[\sum B,\,X]$ for any space  $B$ . Some results on the
$B$ . Some results on the 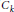 ${{C}_{k}}$ -space are generalized to the
${{C}_{k}}$ -space are generalized to the 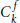 $C_{k}^{f}$ -space for a map
$C_{k}^{f}$ -space for a map 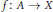 $f\,:\,A\,\to \,X$ . Projective spaces, lens spaces and spaces with a few cells are studied as examples of
$f\,:\,A\,\to \,X$ . Projective spaces, lens spaces and spaces with a few cells are studied as examples of 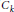 ${{C}_{k}}$ -spaces, and non-
${{C}_{k}}$ -spaces, and non- 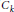 ${{C}_{k}}$ -spaces.
${{C}_{k}}$ -spaces.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
- 2
- Cited by

