How few three-term arithmetic progressions can a subset 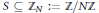$S\,\subseteq \,{{\mathbb{Z}}_{N}}\,:=\,\mathbb{Z}\,/\,N\mathbb{Z}$ have if 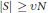$|S|\,\ge \,\upsilon N$ (that is, $S$ has density at least $\upsilon$ )? Varnavides showed that this number of arithmetic progressions is at least 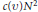$c(v)\,{{N}^{2}}$ for sufficiently large integers 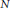$N$ . It is well known that determining good lower bounds for 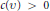$c\left( \upsilon\right)\,>\,0$ is at the same level of depth as Erdös's famous conjecture about whether a subset $T$ of the naturals where 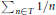$\sum{_{n\in T}\,1/n}$ diverges, has a $k$ -term arithmetic progression for 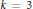$k\,=\,3$ (that is, a three-term arithmetic progression).

We answer a question posed by B. Green about how this minimial number of progressions oscillates for a fixed density $\upsilon$ as 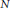$N$ runs through the primes, and as 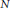$N$ runs through the odd positive integers.