Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Duman, Oktay
and
Özarslan, M. Ali
2007.
Szász–Mirakjan type operators providing a better error estimation.
Applied Mathematics Letters,
Vol. 20,
Issue. 12,
p.
1184.
Rempulska, Lucyna
and
Skorupka, Mariola
2009.
On Approximation by Post-Widder and Stancu Operators Preserving x2.
Kyungpook mathematical journal,
Vol. 49,
Issue. 1,
p.
57.
Ali Özarslan, M.
Duman, Oktay
and
Kaanoğlu, Cem
2010.
Rates of convergence of certain King-type operators for functions with derivative of bounded variation.
Mathematical and Computer Modelling,
Vol. 52,
Issue. 1-2,
p.
334.
Doğru, Ogün
and
Örkcü, Mediha
2010.
Statistical approximation by a modification ofq-Meyer-König and Zeller operators.
Applied Mathematics Letters,
Vol. 23,
Issue. 3,
p.
261.
Siddiqui, Mohammad Arif
and
Agrawal, Raksha Rani
2011.
A Voronovskaya Type Theorem on Modified Post-Widder Operators Preserving x2.
Kyungpook mathematical journal,
Vol. 51,
Issue. 1,
p.
87.
Özarslan, Mehmet Ali
and
Aktuğlu, Hüseyin
2011.
A-statistical approximation of generalized Szász–Mirakjan–Beta operators.
Applied Mathematics Letters,
Vol. 24,
Issue. 11,
p.
1785.
Özarslan, M. Ali
Duman, Oktay
and
Mahmudov, Nazım I.
2011.
Local Approximation Properties of Modified Baskakov Operators.
Results in Mathematics,
Vol. 59,
Issue. 1-2,
p.
1.
Örkcü, Mediha
and
Doğru, Ogün
2011.
q-Szász–Mirakyan–Kantorovich type operators preserving some test functions.
Applied Mathematics Letters,
Vol. 24,
Issue. 9,
p.
1588.
Verma, D.K.
Gupta, Vijay
and
Agrawal, P.N.
2012.
Some approximation properties of Baskakov–Durrmeyer–Stancu operators.
Applied Mathematics and Computation,
Vol. 218,
Issue. 11,
p.
6549.
Deo, Naokant
2012.
Faster rate of convergence on Srivastava–Gupta operators.
Applied Mathematics and Computation,
Vol. 218,
Issue. 21,
p.
10486.
Cárdenas-Morales, D.
Garrancho, P.
and
Raşa, I.
2014.
Approximation properties of Bernstein–Durrmeyer type operators.
Applied Mathematics and Computation,
Vol. 232,
Issue. ,
p.
1.
Finta, Zoltán
2014.
Note on a Korovkin-type theorem.
Journal of Mathematical Analysis and Applications,
Vol. 415,
Issue. 2,
p.
750.
Acar, Tuncer
Aral, Ali
and
Gupta, Vijay
2015.
On Approximation Properties of a New Type of Bernstein-Durrmeyer Operators.
Mathematica Slovaca,
Vol. 65,
Issue. 5,
p.
1107.
Gavrea, Ioan
and
Ivan, Mircea
2018.
Complete asymptotic expansions related to conjecture on a Voronovskaja-type theorem.
Journal of Mathematical Analysis and Applications,
Vol. 458,
Issue. 1,
p.
452.
Braha, Naim L.
Mansour, Toufik
and
Mursaleen, M.
2021.
Approximation by Modified Meyer–König and Zeller Operators via Power Series Summability Method.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 44,
Issue. 4,
p.
2005.
Mishra, Vishnu Narayan
and
Yadav, Rishikesh
2022.
Approximation on a new class of Szász–Mirakjan operators and their extensions in Kantorovich and Durrmeyer variants with applicable properties.
Georgian Mathematical Journal,
Vol. 29,
Issue. 2,
p.
245.
Yingdian, Ma
Weimeng, Wang
and
Jan, Naeem
2023.
The Approximation of a Modified Baskakov Operator.
Journal of Mathematics,
Vol. 2023,
Issue. ,
p.
1.
Kara, Mustafa
and
Özarslan, Mehmet Ali
2024.
Parametric generalization of the q-Meyer–König–Zeller operators.
Chaos, Solitons & Fractals,
Vol. 185,
Issue. ,
p.
115077.
Ayari, M.
2024.
King type modification of q-Szász-Mirakjan operators.
Filomat,
Vol. 38,
Issue. 23,
p.
8323.
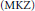 $\left( \text{MKZ} \right)$ operators which preserve the test functions
$\left( \text{MKZ} \right)$ operators which preserve the test functions 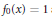 ${{f}_{0}}\left( x \right)=1$ and
${{f}_{0}}\left( x \right)=1$ and 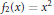 ${{f}_{2}}\left( x \right)={{x}^{2}}$, and we show that this modification provides a better estimation than the classical
${{f}_{2}}\left( x \right)={{x}^{2}}$, and we show that this modification provides a better estimation than the classical 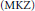 $\left( \text{MKZ} \right)$ operators on the interval
$\left( \text{MKZ} \right)$ operators on the interval 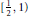 $\left[ \frac{1}{2},1 \right)$ with respect to the modulus of continuity and the Lipschitz class functionals. Furthermore, we present the
$\left[ \frac{1}{2},1 \right)$ with respect to the modulus of continuity and the Lipschitz class functionals. Furthermore, we present the 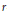 $r$-th order generalization of our operators and study their approximation properties.
$r$-th order generalization of our operators and study their approximation properties.