Hostname: page-component-7dd5485656-gs9qr Total loading time: 0 Render date: 2025-10-31T20:16:30.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Multilinear Proofs for Convolution Estimates for Degenerate Plane Curves

Published online by Cambridge University Press:  20 November 2018

Jong-Guk Bak
Jong-Guk Bak*
Affiliation:
Department of Mathematics Pohang University of Science and Technology Pohang 790-784 Korea, email: bak@euclid.postech.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 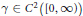$\gamma \in {{C}^{2}}\left( \left[ 0,\infty\right]) \right)$ is a real-valued function such that 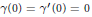$\gamma \left( 0 \right)\,=\,{\gamma }'\left( 0 \right)\,=\,0$ , and 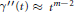${\gamma }''\left( t \right)\,\approx \,{{t}^{m-2}}$ , for some integer 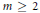$m\,\ge \,2$ . Let 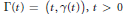$\Gamma \left( t \right)\,=\,\left( t,\,\gamma \left( t \right) \right),\,t\,>\,0$ , be a curve in the plane, and let 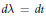$d\text{ }\!\!\lambda\!\!\text{ }\,\text{=}\,dt$ be a measure on this curve. For a function 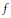$f$ on 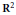${{\mathbf{R}}^{2}}$ , let

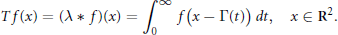$$Tf\left( x \right)\,=\,\left( \text{ }\lambda \text{ }*f \right)\left( x \right)=\int_{0}^{\infty }{f\left( x-\Gamma \left( t \right) \right)dt,\,\,x\in {{\mathbf{R}}^{2}}}.$$

An elementary proof is given for the optimal 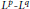${{L}^{p}}-{{L}^{q}}$ mapping properties of $T$ .

Keywords

42A8542B15

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 1 , 01 March 2000 , pp. 17 - 20
Copyright
Copyright © Canadian Mathematical Society 2000

References

[B] Bak, J.-G., Sharp convolution estimates for measures on flat surfaces. J.Math. Anal. Appl. 193 (1995), 756–771.Google Scholar
[BMO] Bak, J.-G., McMichael, D. and Oberlin, D., Convolution estimates for some measures on flat curves. J. Funct. Anal. 101 (1991), 81–96.Google Scholar
[C1] Christ, M., On the restriction of the Fourier transform to curves: endpoint results and the degenerate case. Trans. Amer.Math. Soc. 287 (1985), 223–238.Google Scholar
[C2] Christ, M., Endpoint bounds for singular fractional integral operators. Preprint.Google Scholar
[D1] Drury, S., A survey of k-plane transform estimates. Commutative harmonic analysis (Canton, NY, 1987), 43–55; Contemp.Math. 91, Amer. Math. Soc. Providence, Rhode Island, 1989.Google Scholar
[D2] Drury, S., Degenerate curves and harmonic analysis. Math. Proc. Cambridge Philos. Soc. 108 (1990), 89–96.Google Scholar
[O1] Oberlin, D., Convolution estimates for some measures on curves. Proc.Amer.Math. Soc. 99 (1987), 56–60.Google Scholar
[O2] Oberlin, D., Multilinear proofs for two theorems on circular averages. Colloq.Math. 63 (1992), 187–190.Google Scholar
[O3] Oberlin, D., A convolution estimate for a measure on a curve in R4, II. Proc. Amer. Math. Soc. (to appear).Google Scholar
[RS] Ricci, F. and Stein, E. M., Harmonic analysis on nilpotent groups and singular integrals III: fractional integration along manifolds. J. Funct. Anal. 86 (1989), 360–389.Google Scholar
[Se] Secco, S., Fractional integration along homogeneous curves in R3. Preprint.Google Scholar