Hostname: page-component-7dd5485656-pnlb5 Total loading time: 0.001 Render date: 2025-10-30T18:51:43.619Z Has data issue: false hasContentIssue false
  • English
  • Français

A new upper bound for the asymptotic dimension of RACGs

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  04 October 2023

Panagiotis Tselekidis Open the ORCID record for Panagiotis Tselekidis [Opens in a new window]
Panagiotis Tselekidis*
Affiliation:
Department of Mathematics, Ecole Normale Superieure, 45 Rue d'Ulm, 75005 Paris, France
*
e-mail: panagiotis.tselekidis@queens.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 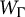$W_{\Gamma} $ be the right-angled Coxeter group with defining graph 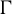$\Gamma $. We show that the asymptotic dimension of 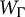$W_{\Gamma} $ is smaller than or equal to 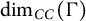$\mathrm{dim}_{CC}(\Gamma )$, the clique-connected dimension of the graph. We generalize this result to graph products of finite groups.

Keywords

Geometric group theoryRACGsasymptotic dimensionclique-connected dimension

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20F69: Asymptotic properties of groups

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 2 , June 2024 , pp. 338 - 349
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bell, G. and Dranishnikov, A., On asymptotic dimension of groups acting on trees . Geom. Dedicata 103(2004), 89–101.CrossRefGoogle Scholar
Bell, G. C., Dranishnikov, A. N., and Keesling, J. E., On a formula for the asymptotic dimension of free products . Fund. Math. 183(2004), no. 1, 39–45.CrossRefGoogle Scholar
Davis, M. W., The geometry and topology of Coxeter groups, London Mathematical Society Monographs Series, 32, Princeton University Press, Princeton, NJ, 2008.Google Scholar
Dirac, G. A., On rigid circuit graphs . Abh. Math. Sem. Univ. Hamburg 25(1961), 71–76.CrossRefGoogle Scholar
Dranishnikov, A., On asymptotic dimension of amalgamated products and right-angled Coxeter groups . Algebr. Geom. Topol. 8(2008), no. 3, 1281–1293.CrossRefGoogle Scholar
Dranishnikov, A., Cohomological approach to asymptotic dimension. Geom. Dedicata 141(2009), 59. https://doi.org/1007/s10711-008-9343-0CrossRefGoogle Scholar
Elements de mathematique, Fasc. XXXIV. Groupes et algebres de Lie. Chapitre IV: Groupes de Coxeter et systemes de Tits. Chapitre V: Groupes engendres par des reflexions. Chapitre VI: Systemes de racines. Actualites Scientifiques et Industrielles, No. 1337, Hermann, Paris, 1968.Google Scholar
Gentimis, T., Asymptotic dimension of finitely presented groups . Proc. Amer. Math. Soc. 136(2008), no. 12, 4103–4110.CrossRefGoogle Scholar
Green, E. R., Graph products of groups. PhD thesis, The University of Leeds, 1990.Google Scholar
Januszkiewicz, T., For Coxeter groups ${z}^{\mid g\mid }$ is a coefficient of a uniformly bounded representation . Fund. Math. 174(2002), no. 1, 79–86.CrossRefGoogle Scholar
Lohrey, M. and Senizergues, G., When is a graph product of groups virtually-free? Comm. Algebra 35(2007), no. 2, 617–621.CrossRefGoogle Scholar
Pullman, N. J., Shank, H., and Wallis, W. D., Clique coverings of graphs V: Maximal-clique partitions . Bull. Aust. Math. Soc. 25(1982), no. 3, 337–356.CrossRefGoogle Scholar
Tselekidis, P., Asymptotic dimension of graphs of groups and one relator groups. To appear in the journal of Algebraic and Geometric Topology. Preprint, 2019. arxiv:1905.07925 Google Scholar