Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-15T07:21:33.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Generalized Schreier Extensions of Groups

Published online by Cambridge University Press:  20 November 2018

Willem Kuyk
Willem Kuyk*
Affiliation:
Mathematical Centre, Amsterdam and McGill University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a (generalized) Schreier extension we mean a group G decomposed into a subinvariant series Gn ↣ Gn-1 ↣ Gn-2 … ↣ G1 ↣ G0 = Gn is anti-invariant in G, i. e. the only subgroup of G which is normal in Gn is the trivial one. ( “ ↣ ” denotes a group monomorphism, i. e. an injection homomorphism. ) As is well known, such groups G can be embedded into the repeated wreath product 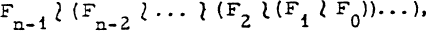where Fi ≅ Gi / Gi+1 (cf. [ 2 ], notation of M. Hall [ 1 ], p. 81).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 1 , April 1966 , pp. 43 - 47
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Hall, M., The theory of groups, McMillan 1959.Google Scholar
2. Krasner, M. - Kaloujnine, L., Produits complet de groupes de permutations et problème d' extension de groupes. Acta Szeged, 14, 1951, 69-82.Google Scholar
3. Neumann, B.H., Hanna, Neumann and Neumann, Peter M., Wreath products and varieties of groups, Math. Z. 80, 44-62 (1962).Google Scholar
4. Vain der Waerden, B. L., Algebra I. Springer 1955.Google Scholar