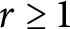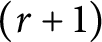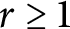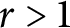1 Introduction
Let K be a compact space, and let r be a positive integer. Following [Reference Bojańczyk, Kopczyński and Toruńczyk2], we say that a function
![]() $f:[S]^r\rightarrow K$
converges to
$f:[S]^r\rightarrow K$
converges to
![]() $p \in K$
if for every neighborhood U of p, there is a finite set F such that
$p \in K$
if for every neighborhood U of p, there is a finite set F such that
![]() $f ([S\backslash F]^r) \subseteq U$
. Once this happens for some p, we say that f is convergent.
$f ([S\backslash F]^r) \subseteq U$
. Once this happens for some p, we say that f is convergent.
This notion, for
![]() $r=2$
, was introduced in [Reference Bojańczyk, Kopczyński and Toruńczyk2] where the special case of our Theorem 2.1 was stated and proved. Their main motivation was to obtain idempotents in compact semigroups K as limits of certain functions
$r=2$
, was introduced in [Reference Bojańczyk, Kopczyński and Toruńczyk2] where the special case of our Theorem 2.1 was stated and proved. Their main motivation was to obtain idempotents in compact semigroups K as limits of certain functions
![]() $f:[\omega ]^2\rightarrow K$
. We show that a more general notion of a space satisfying the r-Ramsey property (Definition 2.1) given below is a quite natural strengthening of sequential compactness, and the main motivation of this paper is to prove some basic facts about this class of spaces and describe some examples showing that r-Ramsey can be strictly weaker than
$f:[\omega ]^2\rightarrow K$
. We show that a more general notion of a space satisfying the r-Ramsey property (Definition 2.1) given below is a quite natural strengthening of sequential compactness, and the main motivation of this paper is to prove some basic facts about this class of spaces and describe some examples showing that r-Ramsey can be strictly weaker than
![]() $(r+1)$
-Ramsey.
$(r+1)$
-Ramsey.
Our topological terminology is standard, and basic definitions and notions can be found in [Reference Engelking3]. Set-theoretic notation and terminology, including some background on Ramsey’s theorem, can be found in [Reference Kunen5], and for a more detailed analysis of almost disjoint families,
![]() $\Psi $
spaces, and the ideals FIN
$\Psi $
spaces, and the ideals FIN
![]() ${}^n$
, we refer the reader to [Reference Hrušak, Hart, van Mill and Simon4].
${}^n$
, we refer the reader to [Reference Hrušak, Hart, van Mill and Simon4].
2 A sequential Ramsey theorem
Theorem 2.1 Let
![]() $(K, \rho )$
be a compact metric space, and let
$(K, \rho )$
be a compact metric space, and let
![]() $f:[\omega ]^r \rightarrow K$
be an arbitrary function, where
$f:[\omega ]^r \rightarrow K$
be an arbitrary function, where
![]() $r>0$
is a natural number. Then there exists an infinite set
$r>0$
is a natural number. Then there exists an infinite set
![]() $B \subseteq \omega $
such that
$B \subseteq \omega $
such that
![]() $f \upharpoonright [B]^r$
converges to some element of K.
$f \upharpoonright [B]^r$
converges to some element of K.
Proof For each
![]() $n\in \omega $
, choose a finite cover
$n\in \omega $
, choose a finite cover
![]() ${\mathcal U}_n$
of K consisting of balls of radius
${\mathcal U}_n$
of K consisting of balls of radius
![]() $2^{-n}$
. Then
$2^{-n}$
. Then
![]() ${\mathcal U}_n$
induces a finite coloring of
${\mathcal U}_n$
induces a finite coloring of
![]() $[\omega ]^r$
. Inductively, choose infinite sets
$[\omega ]^r$
. Inductively, choose infinite sets
![]() $\omega \supseteq A_0 \supseteq A_1 \supseteq \cdots $
such that
$\omega \supseteq A_0 \supseteq A_1 \supseteq \cdots $
such that
![]() $A_n$
is monochromatic for the coloring induced by
$A_n$
is monochromatic for the coloring induced by
![]() $\mathcal {U}_n$
(here we have used the classical Ramsey’s theorem). Let B be any infinite set such that
$\mathcal {U}_n$
(here we have used the classical Ramsey’s theorem). Let B be any infinite set such that
![]() $B \backslash A_n$
is finite for every
$B \backslash A_n$
is finite for every
![]() $n\in \omega $
. By compactness,
$n\in \omega $
. By compactness,
![]() $f \upharpoonright [A]^r$
is convergent.▪
$f \upharpoonright [A]^r$
is convergent.▪
The result above motivates the following definition.
Definition 2.1 Let X be a topological space, and let
![]() $r \in \omega $
be positive. We shall say that X has the r-Ramsey property (or X is an r-Ramsey space) if for every function
$r \in \omega $
be positive. We shall say that X has the r-Ramsey property (or X is an r-Ramsey space) if for every function
![]() $f : [\omega ]^r\rightarrow X$
, there exist
$f : [\omega ]^r\rightarrow X$
, there exist
![]() $p \in X$
and an infinite set
$p \in X$
and an infinite set
![]() $B \subseteq \omega $
such that
$B \subseteq \omega $
such that
![]() $f \upharpoonright [B]^r$
converges to p. We shall say that X has the Ramsey property if it has the r-Ramsey property for every positive
$f \upharpoonright [B]^r$
converges to p. We shall say that X has the Ramsey property if it has the r-Ramsey property for every positive
![]() $r \in \omega $
. We will say that the restriction
$r \in \omega $
. We will say that the restriction
![]() $f\upharpoonright B$
is a convergent subsequence of f.
$f\upharpoonright B$
is a convergent subsequence of f.
Recall that a topological space X is sequentially compact if every sequence in X has a convergent subsequence, and so the
![]() $1$
-Ramsey property is just sequential compactness.
$1$
-Ramsey property is just sequential compactness.
Proposition 2.2 Every space with the r-Ramsey property has the
![]() $(r-1)$
-Ramsey property, whenever
$(r-1)$
-Ramsey property, whenever
![]() $r>1$
. In particular, every space with the r-Ramsey property for some
$r>1$
. In particular, every space with the r-Ramsey property for some
![]() $r>0$
is sequentially compact.
$r>0$
is sequentially compact.
Proof Assume X has the r-Ramsey property, and fix
![]() $g:[\omega ]^{r-1}\rightarrow X$
. Define
$g:[\omega ]^{r-1}\rightarrow X$
. Define
![]() $f [\omega ]^{r}\rightarrow X$
by setting
$f [\omega ]^{r}\rightarrow X$
by setting
![]() $f(s)=g(s \backslash {\max s})$
. Let
$f(s)=g(s \backslash {\max s})$
. Let
![]() $A \in [\omega ]^\omega $
be such that
$A \in [\omega ]^\omega $
be such that
![]() $f \upharpoonright [A]^r$
converges to
$f \upharpoonright [A]^r$
converges to
![]() $p \in X$
.
$p \in X$
.
Fix a neighborhood U of p. There is
![]() $F \in [A]^{<\aleph _0}$
such that
$F \in [A]^{<\aleph _0}$
such that
![]() $f(t) \in U$
whenever
$f(t) \in U$
whenever
![]() $t \subseteq A \backslash F$
and
$t \subseteq A \backslash F$
and
![]() $|t|=r$
. Thus, if
$|t|=r$
. Thus, if
![]() $s \in [A \backslash F]^{r-1}$
, and k is any element of A above s, then
$s \in [A \backslash F]^{r-1}$
, and k is any element of A above s, then
![]() $g(s) = f(s \cup \{k\}) \in U$
.▪
$g(s) = f(s \cup \{k\}) \in U$
.▪
It is useful to note that if
![]() $f:[S]^r\rightarrow X$
converges in a sequentially compact X, then f has a somewhat nice canonical subsequence.
$f:[S]^r\rightarrow X$
converges in a sequentially compact X, then f has a somewhat nice canonical subsequence.
Definition 2.2 A function
![]() $f:[S]^r\rightarrow X$
being r-nice is defined recursively.
$f:[S]^r\rightarrow X$
being r-nice is defined recursively.
A
![]() $f:[S]^1\rightarrow X$
is
$f:[S]^1\rightarrow X$
is
![]() $1$
-nice if it is convergent. For
$1$
-nice if it is convergent. For
![]() $r>1$
,
$r>1$
,
![]() $f:[S]^r\rightarrow X$
is r-nice if:
$f:[S]^r\rightarrow X$
is r-nice if:
-
(1) f is convergent to, say, x,
-
(2) for every
 $s\in [S]^{r-1}$
, the sequence
$s\in [S]^{r-1}$
, the sequence
 $\{f(s\cup \{n\}):n\in S\backslash s\}$
is convergent to a point
$\{f(s\cup \{n\}):n\in S\backslash s\}$
is convergent to a point
 $x_s$
, and
$x_s$
, and -
(3)
 $g:[S]^{r-1}$
defined by
$g:[S]^{r-1}$
defined by
 $g(s)=x_s$
is
$g(s)=x_s$
is
 $(r-1)$
-nice.
$(r-1)$
-nice.
Note that the fact that g, as defined in the definition, is convergent and converges to x follows from the convergence of f to x.
Lemma 2.3 If X is sequentially compact, then any convergent
![]() $f:[S]^r\rightarrow X$
has an r-nice convergent subsequence.
$f:[S]^r\rightarrow X$
has an r-nice convergent subsequence.
Proof By induction on r. If
![]() $r=1$
, then this follows because X is sequentially compact. Fix
$r=1$
, then this follows because X is sequentially compact. Fix
![]() $r>1$
and
$r>1$
and
![]() $f:[S]^r\rightarrow X$
convergent to some point
$f:[S]^r\rightarrow X$
convergent to some point
![]() $x\in X$
. Enumerate
$x\in X$
. Enumerate
![]() $[S]^{r-1}$
as
$[S]^{r-1}$
as
![]() $\{s_k:k\in \omega \}$
. Define
$\{s_k:k\in \omega \}$
. Define
![]() $S_k$
recursively.
$S_k$
recursively.
![]() $S_0\subseteq S$
is such that
$S_0\subseteq S$
is such that
![]() $\{f(s\cup \{n\}):n\in S_0\backslash s_0\}$
converges to
$\{f(s\cup \{n\}):n\in S_0\backslash s_0\}$
converges to
![]() $x_{s_0}$
. Moreover, in general,
$x_{s_0}$
. Moreover, in general,
![]() $S_{k+1}\subseteq S_k$
is chosen such that
$S_{k+1}\subseteq S_k$
is chosen such that
![]() $\{f(s_k\cup \{n\}):n\in S_{k+1}\backslash s_k\}$
converges to some
$\{f(s_k\cup \{n\}):n\in S_{k+1}\backslash s_k\}$
converges to some
![]() $x_{s_{k+1}}$
.
$x_{s_{k+1}}$
.
Now, take T to be a pseudo-intersection of the
![]() $\{S_n:n\in \omega \}$
(i.e., a subset of
$\{S_n:n\in \omega \}$
(i.e., a subset of
![]() $\omega $
such that
$\omega $
such that
![]() $T\backslash S_n$
is finite for each n) and note that
$T\backslash S_n$
is finite for each n) and note that
![]() $g:[T]^{r-1}\rightarrow X$
defined by
$g:[T]^{r-1}\rightarrow X$
defined by
![]() $g(s)=x_s$
is defined, and, because f converges to x, so g also converges to x. Therefore, by our induction hypothesis, g has an
$g(s)=x_s$
is defined, and, because f converges to x, so g also converges to x. Therefore, by our induction hypothesis, g has an
![]() $(r-1)$
-nice subsequence, and the lemma is proved.▪
$(r-1)$
-nice subsequence, and the lemma is proved.▪
It is easy to prove by induction that the closure of the image of an r-nice convergent f is countable and so we have the following corollary:
Corollary 2.4 Assume X is a space with the r-Ramsey property, where
![]() $r \geq 1$
. If
$r \geq 1$
. If
![]() $f:[\omega ]^r\rightarrow X$
, then f has a convergent subsequence
$f:[\omega ]^r\rightarrow X$
, then f has a convergent subsequence
![]() $f\upharpoonright [T]^r: [T]^r\rightarrow X$
such that the closure of
$f\upharpoonright [T]^r: [T]^r\rightarrow X$
such that the closure of
![]() $f([T]^r)$
is countable.
$f([T]^r)$
is countable.
3 Spaces with the Ramsey property
It is clear that the class of all topological spaces with the Ramsey property is stable under closed subspaces and continuous images. The same applies to the r-Ramsey property. In order to see that there are arbitrarily large spaces with the Ramsey property, let
![]() $\kappa $
be any cardinal and consider the
$\kappa $
be any cardinal and consider the
![]() $\Sigma $
-product
$\Sigma $
-product
Note that for any cardinal
![]() $\kappa $
, the closure of every countable subset of
$\kappa $
, the closure of every countable subset of
![]() $\Sigma (\kappa )$
is compact and metrizable; therefore,
$\Sigma (\kappa )$
is compact and metrizable; therefore,
![]() $\Sigma (\kappa )$
has the Ramsey property. More generally, all monolithic countably compact spaces have the Ramsey property (recall that a space X is monolithic if the closure of every countable subset of X is second countable).
$\Sigma (\kappa )$
has the Ramsey property. More generally, all monolithic countably compact spaces have the Ramsey property (recall that a space X is monolithic if the closure of every countable subset of X is second countable).
Recall that the unboundedness number
![]() $\mathfrak {b}$
is the minimal cardinality of a family
$\mathfrak {b}$
is the minimal cardinality of a family
![]() $\mathcal {F} \subseteq \omega ^\omega $
which is unbounded with respect to the almost domination
$\mathcal {F} \subseteq \omega ^\omega $
which is unbounded with respect to the almost domination
![]() $<^*$
, where
$<^*$
, where
![]() $f <^* g$
if
$f <^* g$
if
![]() $f(n) < g(n)$
for all but finitely many
$f(n) < g(n)$
for all but finitely many
![]() $n\in \omega $
.
$n\in \omega $
.
Theorem 3.1 Every sequentially compact space of character
![]() $<\mathfrak {b}$
has the Ramsey property.
$<\mathfrak {b}$
has the Ramsey property.
Proof Suppose X is a sequentially compact space of character
![]() $<\mathfrak {b}$
. We use induction on r to prove that X is r-Ramsey for every
$<\mathfrak {b}$
. We use induction on r to prove that X is r-Ramsey for every
![]() $r\in \omega $
. Sequential compactness says that X is
$r\in \omega $
. Sequential compactness says that X is
![]() $1$
-Ramsey. Suppose
$1$
-Ramsey. Suppose
![]() $r>1$
and we have already proved that X is
$r>1$
and we have already proved that X is
![]() $(r-1)$
-Ramsey. Fix
$(r-1)$
-Ramsey. Fix
![]() $f :[ \omega ]^r\rightarrow X$
.
$f :[ \omega ]^r\rightarrow X$
.
Given
![]() $a \in \omega $
, let
$a \in \omega $
, let
![]() $f_a(s) = f (s \cup \{a\})$
, where
$f_a(s) = f (s \cup \{a\})$
, where
![]() $s \in [ \omega \backslash \{a\}]^{r-1}$
.
$s \in [ \omega \backslash \{a\}]^{r-1}$
.
We construct inductively a sequence
![]() $a_0 < a_1 < \cdots $
in
$a_0 < a_1 < \cdots $
in
![]() $\omega $
, a sequence
$\omega $
, a sequence
![]() $\{p_n:n>0\} \subseteq X$
, and a decreasing sequence of infinite sets
$\{p_n:n>0\} \subseteq X$
, and a decreasing sequence of infinite sets
![]() $\omega = A_0 \supseteq A_1 \supseteq \cdots $
such that:
$\omega = A_0 \supseteq A_1 \supseteq \cdots $
such that:
-
(i)
 $a_n \in A_n$
and
$a_n \in A_n$
and -
(ii)
 $f_{a_n} \upharpoonright [A_{n+1}]^{r-1}$
converges to
$f_{a_n} \upharpoonright [A_{n+1}]^{r-1}$
converges to
 $p_n$
.
$p_n$
.
Suppose
![]() $n>0$
and
$n>0$
and
![]() $a_i$
,
$a_i$
,
![]() $A_i$
, and
$A_i$
, and
![]() $\{p_i:i<n-1\}$
have been constructed for
$\{p_i:i<n-1\}$
have been constructed for
![]() $i<n$
. Using the inductive hypothesis, namely, that X is
$i<n$
. Using the inductive hypothesis, namely, that X is
![]() $(r-1)$
-Ramsey, we find
$(r-1)$
-Ramsey, we find
![]() $p_{n-1} \in X$
and an infinite set
$p_{n-1} \in X$
and an infinite set
![]() $A_n \subseteq A_{n-1}$
such that
$A_n \subseteq A_{n-1}$
such that
![]() $f_{a_{n-1}} \upharpoonright [A_n]^{r-1}$
converges to
$f_{a_{n-1}} \upharpoonright [A_n]^{r-1}$
converges to
![]() $p_{n-1}$
. We set
$p_{n-1}$
. We set
![]() $a_n = \min (A_n \backslash (a_{n-1}+1))$
.
$a_n = \min (A_n \backslash (a_{n-1}+1))$
.
Now, let
![]() $M \in [\omega ]^\omega $
be such that
$M \in [\omega ]^\omega $
be such that
![]() $\{p_n:n \in M\}$
is convergent to some
$\{p_n:n \in M\}$
is convergent to some
![]() $p \in X$
(here we have used the sequential compactness of X). Let
$p \in X$
(here we have used the sequential compactness of X). Let
Re-enumerating
![]() $A_n$
and
$A_n$
and
![]() $p_n$
, we may assume that
$p_n$
, we may assume that
![]() $M = \omega $
.
$M = \omega $
.
Note that the set B has the following property: Given a neighborhood U of p, there is
![]() $m(U) \in \omega $
such that
$m(U) \in \omega $
such that
![]() $\{p_n:n \geq m(U)\} \subseteq U$
. Consequently, for every
$\{p_n:n \geq m(U)\} \subseteq U$
. Consequently, for every
![]() $n \geq m(U)$
, there exists
$n \geq m(U)$
, there exists
![]() $\phi _U(n) \in \omega $
such that
$\phi _U(n) \in \omega $
such that
![]() $f(s) \in U$
whenever
$f(s) \in U$
whenever
![]() $s \in [B]^r$
is such that
$s \in [B]^r$
is such that
![]() $\min s = a_n$
with
$\min s = a_n$
with
![]() $n \geq m(U)$
and
$n \geq m(U)$
and
![]() $\min (s \backslash \{a_n\}) \geq \phi _U(n)$
(the last fact follows from (ii), because
$\min (s \backslash \{a_n\}) \geq \phi _U(n)$
(the last fact follows from (ii), because
![]() $s \backslash \{a_n\} \subseteq A_{n+1}$
). Define
$s \backslash \{a_n\} \subseteq A_{n+1}$
). Define
![]() $\phi _U(n)$
arbitrarily for
$\phi _U(n)$
arbitrarily for
![]() $n<m(U)$
.
$n<m(U)$
.
Let
![]() $\mathcal {U}(p)$
be a fixed local neighborhood base at p such that
$\mathcal {U}(p)$
be a fixed local neighborhood base at p such that
![]() $|\mathcal {U}(p)| < \mathfrak {b}$
. Then
$|\mathcal {U}(p)| < \mathfrak {b}$
. Then
![]() $\{\phi _U:U \in \mathcal {U}(p)\} \subseteq \omega ^\omega $
has cardinality
$\{\phi _U:U \in \mathcal {U}(p)\} \subseteq \omega ^\omega $
has cardinality
![]() $<\mathfrak {b}$
; therefore, we can find a strictly increasing function
$<\mathfrak {b}$
; therefore, we can find a strictly increasing function
![]() $\psi \in B^\omega $
such that
$\psi \in B^\omega $
such that
![]() $\phi _U <^* \psi $
for every
$\phi _U <^* \psi $
for every
![]() $U \in \mathcal {U}(p)$
. Now, let
$U \in \mathcal {U}(p)$
. Now, let
![]() $C = \{\psi (n):n\in \omega \}$
. We claim that C is as required.
$C = \{\psi (n):n\in \omega \}$
. We claim that C is as required.
Fix
![]() $U \in \mathcal {U}(p)$
and fix
$U \in \mathcal {U}(p)$
and fix
![]() $s \in [C]^r$
such that
$s \in [C]^r$
such that
![]() $\min s = a_k$
, where
$\min s = a_k$
, where
![]() $k> m(U)$
and
$k> m(U)$
and
![]() $\psi (n)> \phi _U(n)$
for every
$\psi (n)> \phi _U(n)$
for every
![]() $n \geq k$
. Then
$n \geq k$
. Then
![]() $f(s) = f_{a_k}(s \backslash \{a_k\}) \in U$
. This shows that
$f(s) = f_{a_k}(s \backslash \{a_k\}) \in U$
. This shows that
![]() $f \upharpoonright [B]^r$
converges to p.▪
$f \upharpoonright [B]^r$
converges to p.▪
Corollary 3.2 Let X be a sequentially compact space in which the closure of every countable set is first countable. Then X has the Ramsey property.
Corollary 3.3 Every countably compact linearly ordered space has the Ramsey property.
Concerning products, it is known that the product of countably many sequentially compact spaces is sequentially compact. The same proof can be used to show
Theorem 3.4 The product of countably many r-Ramsey spaces is r-Ramsey.
Proof Suppose we are given r-Ramsey spaces
![]() $X_i$
and
$X_i$
and
 $$ \begin{align*}f:[\omega]^r\rightarrow \prod_{i\in \omega} X_i.\end{align*} $$
$$ \begin{align*}f:[\omega]^r\rightarrow \prod_{i\in \omega} X_i.\end{align*} $$
Recursively choose sets
![]() $B_0\supseteq B_1\supseteq \cdots $
so that for each i,
$B_0\supseteq B_1\supseteq \cdots $
so that for each i,
![]() $\pi _i\circ f:[B_i]^r\rightarrow X_i$
converges to
$\pi _i\circ f:[B_i]^r\rightarrow X_i$
converges to
![]() $x_i$
. Then it is straightforward to see that if B is any pseudo-intersection of the family
$x_i$
. Then it is straightforward to see that if B is any pseudo-intersection of the family
![]() $\{B_i:i\in \omega \}$
, then
$\{B_i:i\in \omega \}$
, then
![]() $f:[B]^r\rightarrow \prod _{i\in \omega } X_i$
converges to
$f:[B]^r\rightarrow \prod _{i\in \omega } X_i$
converges to
![]() $\langle x(i):i<\omega \rangle $
.▪
$\langle x(i):i<\omega \rangle $
.▪
The splitting number,
![]() ${\mathfrak s}$
, can be characterized as the minimal
${\mathfrak s}$
, can be characterized as the minimal
![]() $\kappa $
such that
$\kappa $
such that
![]() $2^\kappa $
is not sequentially compact (see [Reference van Douwen, Kunen and Vaughan7]). The analogous cardinal characteristic of the continuum that characterizes the r-Ramsey property in Cantor cubes is
$2^\kappa $
is not sequentially compact (see [Reference van Douwen, Kunen and Vaughan7]). The analogous cardinal characteristic of the continuum that characterizes the r-Ramsey property in Cantor cubes is
![]() ${\mathfrak {par}}$
and was introduced by Blass in [Reference Blass, Foreman and Kanamori1].
${\mathfrak {par}}$
and was introduced by Blass in [Reference Blass, Foreman and Kanamori1].
Definition 3.1 A set
![]() $A\subseteq \omega $
is almost homogeneous for a partition
$A\subseteq \omega $
is almost homogeneous for a partition
![]() $f:[\omega ]^n\rightarrow 2$
if there is a finite
$f:[\omega ]^n\rightarrow 2$
if there is a finite
![]() $F\subseteq A$
such that f is constant on
$F\subseteq A$
such that f is constant on
![]() $[A\backslash F]^n$
. Furthermore,
$[A\backslash F]^n$
. Furthermore,
![]() ${\mathfrak {par}}_n$
denotes the smallest cardinal
${\mathfrak {par}}_n$
denotes the smallest cardinal
![]() $\kappa $
such that there is a family of partitions of
$\kappa $
such that there is a family of partitions of
![]() $[\omega ]^n\rightarrow 2$
of size
$[\omega ]^n\rightarrow 2$
of size
![]() $\kappa $
such that no infinite set is almost homogeneous for all of them simultaneously.
$\kappa $
such that no infinite set is almost homogeneous for all of them simultaneously.
First, notice that
![]() ${\mathfrak {par}}_1$
is just the splitting number
${\mathfrak {par}}_1$
is just the splitting number
![]() ${\mathfrak s}$
. Moreover, note that if we consider partitions into some finite number of pieces k, instead of two pieces, we obtain the same cardinal. Moreover, the following theorem of Blass shows that for all
${\mathfrak s}$
. Moreover, note that if we consider partitions into some finite number of pieces k, instead of two pieces, we obtain the same cardinal. Moreover, the following theorem of Blass shows that for all
![]() $n\geq 2$
, we have that
$n\geq 2$
, we have that
![]() ${\mathfrak {par}}_n={\mathfrak {par}}_2$
.
${\mathfrak {par}}_n={\mathfrak {par}}_2$
.
Theorem 3.5 [Reference Blass, Foreman and Kanamori1] For each
![]() $n\geq 2$
,
$n\geq 2$
,
![]() ${\mathfrak {par}}_n=\min \{{\mathfrak {b, s}}\}$
.
${\mathfrak {par}}_n=\min \{{\mathfrak {b, s}}\}$
.
Now, we prove that the minimal
![]() $\kappa $
such that
$\kappa $
such that
![]() $2^\kappa $
is not r-Ramsey is precisely
$2^\kappa $
is not r-Ramsey is precisely
![]() $\mathfrak {par}_2$
.
$\mathfrak {par}_2$
.
Theorem 3.6 For each
![]() $\kappa <\mathfrak {par}_2$
,
$\kappa <\mathfrak {par}_2$
,
![]() $2^\kappa $
is r-Ramsey for all
$2^\kappa $
is r-Ramsey for all
![]() $r\in \omega $
. In addition,
$r\in \omega $
. In addition,
![]() $2^{\mathfrak {par}_2}$
is not
$2^{\mathfrak {par}_2}$
is not
![]() $2$
-Ramsey.
$2$
-Ramsey.
Proof Fix
![]() $\kappa <\mathfrak {par}_2$
and fix
$\kappa <\mathfrak {par}_2$
and fix
![]() $f:[\omega ]^r\rightarrow 2^\kappa $
. For each
$f:[\omega ]^r\rightarrow 2^\kappa $
. For each
![]() $\alpha <\kappa $
, let
$\alpha <\kappa $
, let
![]() $f_\alpha =\pi _\alpha \cdot f$
. By the definition of
$f_\alpha =\pi _\alpha \cdot f$
. By the definition of
![]() $\kappa <\mathfrak {par}_2=\mathfrak {par}_r$
, there is
$\kappa <\mathfrak {par}_2=\mathfrak {par}_r$
, there is
![]() $B\subseteq \omega $
and for each
$B\subseteq \omega $
and for each
![]() $\alpha $
an
$\alpha $
an
![]() $i_\alpha $
such that for every
$i_\alpha $
such that for every
![]() $\alpha <\kappa $
, there is a finite set F such that
$\alpha <\kappa $
, there is a finite set F such that
![]() $f_\alpha $
is constant with value
$f_\alpha $
is constant with value
![]() $i_\alpha $
on
$i_\alpha $
on
![]() $[B\backslash F]^r$
. This just means that
$[B\backslash F]^r$
. This just means that
![]() $f:[B]^r\rightarrow 2^\kappa $
converges to
$f:[B]^r\rightarrow 2^\kappa $
converges to
![]() $(i_\alpha )_{\alpha \in \kappa }$
as required.
$(i_\alpha )_{\alpha \in \kappa }$
as required.
To complete the proof, to see that
![]() $2^\kappa $
is not
$2^\kappa $
is not
![]() $2$
-Ramsey for
$2$
-Ramsey for
![]() $\kappa =\mathfrak {par}_2$
, fix a family
$\kappa =\mathfrak {par}_2$
, fix a family
![]() $\{f_\alpha :\alpha <\kappa \}$
so that no
$\{f_\alpha :\alpha <\kappa \}$
so that no
![]() $B\subseteq \omega $
is almost homogeneous for all functions
$B\subseteq \omega $
is almost homogeneous for all functions
![]() $f_\alpha $
. Taking the product function
$f_\alpha $
. Taking the product function
![]() $f=\prod f_\alpha $
we have, as above, that for no B can
$f=\prod f_\alpha $
we have, as above, that for no B can
![]() $f:[B]^2\rightarrow 2^\kappa $
converge.▪
$f:[B]^2\rightarrow 2^\kappa $
converge.▪
Corollary 3.7 If
![]() $\mathfrak {b}<\mathfrak {s}$
, then
$\mathfrak {b}<\mathfrak {s}$
, then
![]() $2^{\mathfrak b}$
is sequentially compact but not
$2^{\mathfrak b}$
is sequentially compact but not
![]() $2$
-Ramsey.
$2$
-Ramsey.
4 Examples
In this section, we give some examples of spaces with the k-Ramsey property that do not have the
![]() $(k+1)$
-Ramsey property. The first example of a
$(k+1)$
-Ramsey property. The first example of a
![]() $1$
-Ramsey (i.e., sequentially compact) not
$1$
-Ramsey (i.e., sequentially compact) not
![]() $2$
-Ramsey is in ZFC, but for larger k, we assume the Continuum Hypothesis (CH). All of the examples are of the form
$2$
-Ramsey is in ZFC, but for larger k, we assume the Continuum Hypothesis (CH). All of the examples are of the form
![]() $K({\mathcal A})=\alpha (\Psi (\mathcal {A}))$
, the Alexandrov–Urysohn compactum formed by taking the one-point compactification of the
$K({\mathcal A})=\alpha (\Psi (\mathcal {A}))$
, the Alexandrov–Urysohn compactum formed by taking the one-point compactification of the
![]() $\Psi $
-space determined by an almost disjoint family
$\Psi $
-space determined by an almost disjoint family
![]() $\mathcal {A}$
of infinite subsets of
$\mathcal {A}$
of infinite subsets of
![]() $\omega $
. Infinite sets
$\omega $
. Infinite sets
![]() $a,b\subseteq \omega $
are said to be almost disjoint if
$a,b\subseteq \omega $
are said to be almost disjoint if
![]() $a\cap b$
is finite. If
$a\cap b$
is finite. If
![]() ${\mathcal A}$
is a family of subsets of
${\mathcal A}$
is a family of subsets of
![]() $\omega $
that are pairwise almost disjoint, then the space
$\omega $
that are pairwise almost disjoint, then the space
![]() $\Psi (\mathcal {A})=\omega \cup {\mathcal A}$
where the points of
$\Psi (\mathcal {A})=\omega \cup {\mathcal A}$
where the points of
![]() $\omega $
are isolated and a neighborhood base for
$\omega $
are isolated and a neighborhood base for
![]() $a\in {\mathcal A}$
is given by sets of the form
$a\in {\mathcal A}$
is given by sets of the form
![]() $\{a\}\cup (a\backslash n)$
. It is well known that
$\{a\}\cup (a\backslash n)$
. It is well known that
![]() $K({\mathcal A})$
, the one-point compactification of
$K({\mathcal A})$
, the one-point compactification of
![]() $\Psi ({\mathcal A})$
, is sequentially compact (see [Reference Hrušak, Hart, van Mill and Simon4] for more on almost disjoint families and
$\Psi ({\mathcal A})$
, is sequentially compact (see [Reference Hrušak, Hart, van Mill and Simon4] for more on almost disjoint families and
![]() $\Psi $
-spaces).
$\Psi $
-spaces).
If
![]() $\mathcal {A}$
is a maximal almost disjoint (mad) family, then
$\mathcal {A}$
is a maximal almost disjoint (mad) family, then
![]() $K(\mathcal {A})$
is not even
$K(\mathcal {A})$
is not even
![]() $2$
-Ramsey.
$2$
-Ramsey.
Example 4.1 Let
![]() $\mathcal {A}$
be an infinite maximal almost disjoint family on
$\mathcal {A}$
be an infinite maximal almost disjoint family on
![]() $[\omega ]^\omega $
. Then the Alexandrov–Urysohn compactum
$[\omega ]^\omega $
. Then the Alexandrov–Urysohn compactum
![]() $K(\mathcal {A})$
is a compact and sequentially compact space failing the
$K(\mathcal {A})$
is a compact and sequentially compact space failing the
![]() $2$
-Ramsey property.
$2$
-Ramsey property.
Proof For convenience, we assume that
![]() $\mathcal {A} \subseteq [\omega \times \omega ]^\omega $
and
$\mathcal {A} \subseteq [\omega \times \omega ]^\omega $
and
![]() $\{n\} \times \omega \in \mathcal {A}$
for each
$\{n\} \times \omega \in \mathcal {A}$
for each
![]() $n \in \omega $
. Thus,
$n \in \omega $
. Thus,
where we write
![]() $p_n$
instead of
$p_n$
instead of
![]() $p_{\{n\} \times \omega }$
. Then
$p_{\{n\} \times \omega }$
. Then
![]() $\omega \times \omega $
is the set of isolated points,
$\omega \times \omega $
is the set of isolated points,
![]() $K(\mathcal {A}) \backslash \{\infty \}$
is locally compact, and a basic neighborhood of
$K(\mathcal {A}) \backslash \{\infty \}$
is locally compact, and a basic neighborhood of
![]() $p_A$
is
$p_A$
is
![]() $\{p_A\} \cup (A \backslash F)$
, where
$\{p_A\} \cup (A \backslash F)$
, where
![]() $F \in [A]^{<\omega }$
.
$F \in [A]^{<\omega }$
.
Let
![]() $f:[\omega ]^2\rightarrow K(\mathcal {A})$
be defined by
$f:[\omega ]^2\rightarrow K(\mathcal {A})$
be defined by
![]() $f(\{k,{\textit {l}}\}) = \langle k,{\textit {l}}\rangle $
, where
$f(\{k,{\textit {l}}\}) = \langle k,{\textit {l}}\rangle $
, where
![]() $k < {\textit {l}}$
. Now, it is easy to see that this f witnesses the failure of
$k < {\textit {l}}$
. Now, it is easy to see that this f witnesses the failure of
![]() $2$
-Ramsey, because for any
$2$
-Ramsey, because for any
![]() $S\subseteq \omega $
infinite, the closure of
$S\subseteq \omega $
infinite, the closure of
![]() $f([B]^2)$
in
$f([B]^2)$
in
![]() $\Psi (\mathcal {A})$
is infinite, and because
$\Psi (\mathcal {A})$
is infinite, and because
![]() $\mathcal {A}$
is mad, it follows that the closure is uncountable. Therefore, by Corollary 2.4,
$\mathcal {A}$
is mad, it follows that the closure is uncountable. Therefore, by Corollary 2.4,
![]() $K(\mathcal {A})$
cannot be
$K(\mathcal {A})$
cannot be
![]() $2$
-Ramsey.
$2$
-Ramsey.
We now describe, for each
![]() $r>1$
, an r-Ramsey not
$r>1$
, an r-Ramsey not
![]() $(r+1)$
-Ramsey compact space of the form
$(r+1)$
-Ramsey compact space of the form
![]() $K(\mathcal {A})$
. We state a few lemmas about these properties in these types of spaces.■
$K(\mathcal {A})$
. We state a few lemmas about these properties in these types of spaces.■
Lemma 4.2 For any almost disjoint family
![]() $\mathcal {A}$
on a countable set I of isolated points,
$\mathcal {A}$
on a countable set I of isolated points,
![]() $K(\mathcal {A})$
is r-Ramsey if and only if for any
$K(\mathcal {A})$
is r-Ramsey if and only if for any
![]() $f:[\omega ]^r\rightarrow I$
, there is
$f:[\omega ]^r\rightarrow I$
, there is
![]() $B\subseteq \omega $
such that
$B\subseteq \omega $
such that
![]() $f\upharpoonright [B]^r$
converges.
$f\upharpoonright [B]^r$
converges.
Proof The property is clearly necessary. For sufficiency, note that for any
![]() $f:[\omega ]^r\rightarrow K(\mathcal {A})$
, one can find B such that either
$f:[\omega ]^r\rightarrow K(\mathcal {A})$
, one can find B such that either
![]() $f([B]^r)\subseteq \mathcal {A}$
(in which case, because any infinite subset converges, one can easily find
$f([B]^r)\subseteq \mathcal {A}$
(in which case, because any infinite subset converges, one can easily find
![]() $B'\subseteq B$
witnessing r-Ramsey) or
$B'\subseteq B$
witnessing r-Ramsey) or
![]() $f([B]^r)\subseteq I$
, as required.▪
$f([B]^r)\subseteq I$
, as required.▪
Lemma 4.3
![]() $K(\mathcal {A})$
is r-Ramsey if for every
$K(\mathcal {A})$
is r-Ramsey if for every
![]() $f:[\omega ]^r\rightarrow I$
, there is an infinite
$f:[\omega ]^r\rightarrow I$
, there is an infinite
![]() $B\subseteq \omega $
such that
$B\subseteq \omega $
such that
is of size less than
![]() ${\mathfrak b}$
.
${\mathfrak b}$
.
Proof If we can find such a B, then the closure of the subset
![]() $f([B]^r)$
in
$f([B]^r)$
in
![]() $K(\mathcal {A})$
has countable character at all points of
$K(\mathcal {A})$
has countable character at all points of
![]() $\mathcal {A}$
and character less than
$\mathcal {A}$
and character less than
![]() ${\mathfrak b}$
at
${\mathfrak b}$
at
![]() $\infty $
, and so by Theorem 3.1, this subspace is r-Ramsey, and so we can find
$\infty $
, and so by Theorem 3.1, this subspace is r-Ramsey, and so we can find
![]() $B'\subseteq B$
on which f converges.▪
$B'\subseteq B$
on which f converges.▪
We now turn to a construction of an r-Ramsey example of an Alexandrov–Urysohn compactum that is not
![]() $(r+1)$
-Ramsey.
$(r+1)$
-Ramsey.
We first need some basic properties of the Fubini product of the ideal FIN. Recall that FIN is the ideal of finite subsets of
![]() $\omega $
and, for each
$\omega $
and, for each
![]() $n>1$
, FIN
$n>1$
, FIN
![]() ${}^n$
is the ideal on
${}^n$
is the ideal on
![]() $\omega ^n$
defined recursively by
$\omega ^n$
defined recursively by
The following lemma is easily proved using the definition.
Lemma 4.4 For any
![]() $X\subseteq \omega ^n$
, if
$X\subseteq \omega ^n$
, if
![]() $X\not \in \text {FIN}^n$
, then there is a
$X\not \in \text {FIN}^n$
, then there is a
![]() $T\subseteq X$
such that T forms an everywhere
$T\subseteq X$
such that T forms an everywhere
![]() $\omega $
-splitting tree. That is, letting
$\omega $
-splitting tree. That is, letting
![]() $T_i=\{x\upharpoonright i: x\in T\}$
, for each
$T_i=\{x\upharpoonright i: x\in T\}$
, for each
![]() $i<n$
and each
$i<n$
and each
![]() $s\in T_i$
,
$s\in T_i$
,
![]() $\{t\in T_{i+1}:t\upharpoonright i = s\}$
is infinite.
$\{t\in T_{i+1}:t\upharpoonright i = s\}$
is infinite.
Now, we need the following lemma.
Lemma 4.5 For any function
![]() $f:[\omega ]^n\rightarrow \omega ^{n+1}$
, there is a
$f:[\omega ]^n\rightarrow \omega ^{n+1}$
, there is a
![]() $B\subseteq \omega $
infinite such that
$B\subseteq \omega $
infinite such that
![]() $f([B]^n)\in \text {FIN}^{n+1}$
.
$f([B]^n)\in \text {FIN}^{n+1}$
.
Proof By induction on n. When
![]() $n=1$
, we can find B such that
$n=1$
, we can find B such that
![]() $f(B)$
is either contained in a column
$f(B)$
is either contained in a column
![]() $\{k\}\times \omega $
or is a partial function. In either case,
$\{k\}\times \omega $
or is a partial function. In either case,
![]() $f(B)\in \text {FIN}^2$
.
$f(B)\in \text {FIN}^2$
.
For the inductive step, fix
![]() $f:[\omega ]^n\rightarrow \omega ^{n+1}$
and fix
$f:[\omega ]^n\rightarrow \omega ^{n+1}$
and fix
![]() $k_0\in \omega $
arbitrary. Define
$k_0\in \omega $
arbitrary. Define
![]() $f_{k_0}:[\omega \backslash k_0+1]^{n-1}\rightarrow \omega ^{n+1}$
by
$f_{k_0}:[\omega \backslash k_0+1]^{n-1}\rightarrow \omega ^{n+1}$
by
![]() $f_{k_0}(s)=f(\{k_0\}\cup s)$
. By our inductive assumption, there is an infinite
$f_{k_0}(s)=f(\{k_0\}\cup s)$
. By our inductive assumption, there is an infinite
![]() $B_1\subseteq \omega \backslash k_0+1$
such that:
$B_1\subseteq \omega \backslash k_0+1$
such that:
-
(*) the projection of
 $f_{k_0}([B_1]^{n-1})$
onto any n coordinates of
$f_{k_0}([B_1]^{n-1})$
onto any n coordinates of
 $\omega ^{n+1}$
is in FIN
$\omega ^{n+1}$
is in FIN
 ${}^n$
.
${}^n$
.
Let
![]() $k_1=\min (B_1)$
and continue recursively constructing
$k_1=\min (B_1)$
and continue recursively constructing
![]() $\{k_i,B_i\}$
so that for each i,
$\{k_i,B_i\}$
so that for each i,
![]() $k_i=\min (B_i)$
and
$k_i=\min (B_i)$
and
-
(*) the projection of
 $f_{k_i}([B_{i+1}]^{n-1})$
onto any n coordinates of
$f_{k_i}([B_{i+1}]^{n-1})$
onto any n coordinates of
 $\omega ^{n+1}$
is in FIN
$\omega ^{n+1}$
is in FIN
 ${}^n$
.
${}^n$
.
Now, let
![]() $B=\{k_i:i\in \omega \}$
. Since
$B=\{k_i:i\in \omega \}$
. Since
![]() $(\omega +1)^{n+1}$
is r-Ramsey for all r, we may, by possibly shrinking B, assume that
$(\omega +1)^{n+1}$
is r-Ramsey for all r, we may, by possibly shrinking B, assume that
![]() $f:[B]^n\rightarrow (\omega +1)^{n+1}$
converges to some x.
$f:[B]^n\rightarrow (\omega +1)^{n+1}$
converges to some x.
CASE 1.
![]() $x(i)=\omega $
for all
$x(i)=\omega $
for all
![]() $i<n+1$
. In this case, if
$i<n+1$
. In this case, if
![]() $f([B]^n)$
is not in FIN
$f([B]^n)$
is not in FIN
![]() ${}^{n+1}$
, then there is an everywhere
${}^{n+1}$
, then there is an everywhere
![]() $\omega $
-splitting tree
$\omega $
-splitting tree
![]() $T\subseteq f([B]^n)$
witnessing this. Fix
$T\subseteq f([B]^n)$
witnessing this. Fix
![]() $z\in T$
and consider
$z\in T$
and consider
![]() $k=z(0)$
. Since
$k=z(0)$
. Since
![]() $f:[B]^n\rightarrow (\omega +1)^{n+1}$
converges to x, there is an N such that
$f:[B]^n\rightarrow (\omega +1)^{n+1}$
converges to x, there is an N such that
Therefore,
![]() $f([B\backslash N]^n)$
is disjoint from
$f([B\backslash N]^n)$
is disjoint from
![]() $T'=\{s\in T: s(0)<N\}$
. Note that the projection of
$T'=\{s\in T: s(0)<N\}$
. Note that the projection of
![]() $T'$
onto
$T'$
onto
![]() $\omega ^{n+1\backslash \{0\}}$
is not in FIN
$\omega ^{n+1\backslash \{0\}}$
is not in FIN
![]() ${}^n$
. Furthermore,
${}^n$
. Furthermore,
![]() $T'$
is covered by the set
$T'$
is covered by the set
![]() $f(\{s\in [B]^n:\min s < N\})$
, but for each
$f(\{s\in [B]^n:\min s < N\})$
, but for each
![]() $k_i<N$
, the projection of the sets
$k_i<N$
, the projection of the sets
![]() $f(\{s\in [B]^n:\min s =k_i\})$
onto
$f(\{s\in [B]^n:\min s =k_i\})$
onto
![]() $\omega ^{n+1\backslash \{0\}}$
is in FIN
$\omega ^{n+1\backslash \{0\}}$
is in FIN
![]() ${}^n$
, a contradiction.
${}^n$
, a contradiction.
CASE 2. There is i such that
![]() $x(i)\not =\omega $
. In this case, there is some N such that
$x(i)\not =\omega $
. In this case, there is some N such that
In addition, this completes the proof because
![]() $\{z\in (\omega )^{n+1}: z(i)=x(i)\}$
is in FIN
$\{z\in (\omega )^{n+1}: z(i)=x(i)\}$
is in FIN
![]() ${}^{n+1}$
.▪
${}^{n+1}$
.▪
Now, fix
![]() $r>1$
and we will need to assume CH. We build an almost disjoint family
$r>1$
and we will need to assume CH. We build an almost disjoint family
![]() $\mathcal {A}$
on
$\mathcal {A}$
on
![]() $\omega ^{r+1}$
so that for the function
$\omega ^{r+1}$
so that for the function
![]() $G:[\omega ]^{r+1}\rightarrow \omega ^{r+1}$
defined by
$G:[\omega ]^{r+1}\rightarrow \omega ^{r+1}$
defined by
![]() $G(x)=\langle x(0),\ldots ,x(r)\rangle $
where
$G(x)=\langle x(0),\ldots ,x(r)\rangle $
where
![]() $x=\{x(0),\ldots ,x(r)\}$
is the increasing enumeration of x, G will have no convergent subsequence B.
$x=\{x(0),\ldots ,x(r)\}$
is the increasing enumeration of x, G will have no convergent subsequence B.
To simplify some notation for any B, let
Lemma 4.6 Suppose
![]() $\mathcal {A}$
is an almost disjoint family on
$\mathcal {A}$
is an almost disjoint family on
![]() $\omega ^{r+1}$
. For the function G defined as above, B is a convergent subsequence for G with limit
$\omega ^{r+1}$
. For the function G defined as above, B is a convergent subsequence for G with limit
![]() $\infty $
in
$\infty $
in
![]() $K(\mathcal {A})$
if and only if for every
$K(\mathcal {A})$
if and only if for every
![]() $a\in \mathcal {A}$
, there is an n such that
$a\in \mathcal {A}$
, there is an n such that
![]() $a\cap (B\backslash n)^{\uparrow r+1}=\emptyset $
.
$a\cap (B\backslash n)^{\uparrow r+1}=\emptyset $
.
Proof Directly from the definitions.▪
Theorem 4.7 Assume CH. For each
![]() $r>1$
, there is an almost disjoint family
$r>1$
, there is an almost disjoint family
![]() $\mathcal {A}$
on
$\mathcal {A}$
on
![]() $\omega $
such that
$\omega $
such that
![]() $K(\mathcal {A})$
is r-Ramsey but not
$K(\mathcal {A})$
is r-Ramsey but not
![]() $(r+1)$
-Ramsey.
$(r+1)$
-Ramsey.
Proof We will construct
![]() $\mathcal {A}=\{a_\alpha :\alpha <\omega _1\}$
an almost disjoint family on
$\mathcal {A}=\{a_\alpha :\alpha <\omega _1\}$
an almost disjoint family on
![]() $\omega ^{r+1}$
by defining each
$\omega ^{r+1}$
by defining each
![]() $a_\alpha $
by recursion on
$a_\alpha $
by recursion on
![]() $\alpha $
. We start by letting
$\alpha $
. We start by letting
![]() $\{a_n:n\in \omega \}$
be an enumeration of the disjoint family
$\{a_n:n\in \omega \}$
be an enumeration of the disjoint family
Note that each
![]() $a_n\in \text {FIN}^{n+1}$
and
$a_n\in \text {FIN}^{n+1}$
and
-
(*) any x that is almost disjoint from all the
 $a_n$
is also in FIN
$a_n$
is also in FIN
 ${}^{n+1}$
.
${}^{n+1}$
.
We enumerate as
![]() $\{B_\alpha :\omega \leq \alpha <\omega _1\}$
all infinite subsets of
$\{B_\alpha :\omega \leq \alpha <\omega _1\}$
all infinite subsets of
![]() $\omega $
and fix an enumeration
$\omega $
and fix an enumeration
 $$ \begin{align*}\{f_\alpha: \omega \leq \alpha<\omega_1\}=\left(\omega^{r+1}\right)^{[\omega]^r}. \end{align*} $$
$$ \begin{align*}\{f_\alpha: \omega \leq \alpha<\omega_1\}=\left(\omega^{r+1}\right)^{[\omega]^r}. \end{align*} $$
Recall our plan that
![]() $G:[\omega ]^{r+1}\rightarrow \omega ^{r+1}$
should have no convergent subsequence.
$G:[\omega ]^{r+1}\rightarrow \omega ^{r+1}$
should have no convergent subsequence.
Suppose that at some stage
![]() $\alpha $
of the construction, we have defined
$\alpha $
of the construction, we have defined
![]() $\{a_\beta :\beta <\alpha \}$
and infinite sets
$\{a_\beta :\beta <\alpha \}$
and infinite sets
![]() $\{X_\beta :\omega \leq \beta <\alpha \}$
such that:
$\{X_\beta :\omega \leq \beta <\alpha \}$
such that:
-
(1) For all
 $\omega \leq \beta <\alpha $
,
$\omega \leq \beta <\alpha $
,
 $f_\beta ([X_\beta ]^r)\in \text {FIN}^{n+1}$
.
$f_\beta ([X_\beta ]^r)\in \text {FIN}^{n+1}$
. -
(2) For all
 $\beta <\gamma <\alpha $
,
$\beta <\gamma <\alpha $
,
 $a_\beta \cap a_\gamma $
is finite.
$a_\beta \cap a_\gamma $
is finite. -
(3) For all
 $\omega \leq \beta <\gamma <\alpha $
,
$\omega \leq \beta <\gamma <\alpha $
,
 $\left (f_\beta ([X_\beta ]^r)\right )\cap a_\gamma $
is finite.
$\left (f_\beta ([X_\beta ]^r)\right )\cap a_\gamma $
is finite. -
(4) For all
 $\omega \leq \beta <\alpha $
and all
$\omega \leq \beta <\alpha $
and all
 $n<\omega $
,
$n<\omega $
,
 $a_\beta \subseteq ^*G([B_\beta \backslash n]^{r+1})$
.
$a_\beta \subseteq ^*G([B_\beta \backslash n]^{r+1})$
.
To define
![]() $a_\alpha $
and
$a_\alpha $
and
![]() $X_\alpha $
, note first, by clause
$X_\alpha $
, note first, by clause
![]() $(*)$
and (1) above, it follows that
$(*)$
and (1) above, it follows that
 $$ \begin{align*}{\mathcal H}=\{f_\beta([X_\beta]^r):\beta<\alpha\}\cup\{a_\beta:\beta<\alpha\}\subseteq \text{FIN}^{n+1}.\end{align*} $$
$$ \begin{align*}{\mathcal H}=\{f_\beta([X_\beta]^r):\beta<\alpha\}\cup\{a_\beta:\beta<\alpha\}\subseteq \text{FIN}^{n+1}.\end{align*} $$
Therefore, the family
has an infinite pseudo-intersection. Let
![]() $a_\alpha $
be any such pseudo-intersection, and it directly follows that
$a_\alpha $
be any such pseudo-intersection, and it directly follows that
![]() $a_\alpha $
satisfies the inductive hypotheses (2)–(4). Therefore, we need only define
$a_\alpha $
satisfies the inductive hypotheses (2)–(4). Therefore, we need only define
![]() $X_\alpha $
to satisfy (1), but that there is such an
$X_\alpha $
to satisfy (1), but that there is such an
![]() $X_\alpha $
follows from Lemma 4.5.
$X_\alpha $
follows from Lemma 4.5.
This completes the construction of
![]() $\mathcal {A}=\{a_\alpha :\alpha <\omega _1\}$
. To see that it is r-Ramsey, by Lemma 4.2, we need only consider functions
$\mathcal {A}=\{a_\alpha :\alpha <\omega _1\}$
. To see that it is r-Ramsey, by Lemma 4.2, we need only consider functions
![]() $f:[\omega ]^r\rightarrow \omega ^{r+1}$
, and each such f appears as an
$f:[\omega ]^r\rightarrow \omega ^{r+1}$
, and each such f appears as an
![]() $f_\alpha $
. For each
$f_\alpha $
. For each
![]() $\alpha $
by inductive hypothesis (3), we have that
$\alpha $
by inductive hypothesis (3), we have that
is countable. And so by Lemma 4.3, it follows that
![]() $K(\mathcal {A})$
is r-Ramsey. On the other hand, to see that G has no convergent subsequence, first note that if any
$K(\mathcal {A})$
is r-Ramsey. On the other hand, to see that G has no convergent subsequence, first note that if any
![]() $B_\alpha $
were to form a convergent subsequence for G, then it would need to converge to
$B_\alpha $
were to form a convergent subsequence for G, then it would need to converge to
![]() $\infty $
. Indeed, for all n, we have
$\infty $
. Indeed, for all n, we have
 $\{a_k:|a_k\cap G([B_\beta \backslash n]^{r+1})|=\aleph _0\}$
is infinite and so for no n is
$\{a_k:|a_k\cap G([B_\beta \backslash n]^{r+1})|=\aleph _0\}$
is infinite and so for no n is
 $G([B_\beta \backslash n]^{r+1})\subseteq ^*a_\alpha $
for any
$G([B_\beta \backslash n]^{r+1})\subseteq ^*a_\alpha $
for any
![]() $\alpha <\omega _1$
. And now, inductive hypothesis (4) implies, by Lemma 4.6, that no
$\alpha <\omega _1$
. And now, inductive hypothesis (4) implies, by Lemma 4.6, that no
![]() $B_\alpha $
is a convergent subsequence for G and so
$B_\alpha $
is a convergent subsequence for G and so
![]() $K(\mathcal {A})$
is not
$K(\mathcal {A})$
is not
![]() $(r+1)$
-Ramsey.▪
$(r+1)$
-Ramsey.▪
5 Questions
We finish with the following questions.
Question 1 Does there exist a space with the r-Ramsey property and without the
![]() $(r+1)$
-property assuming only ZFC? Here
$(r+1)$
-property assuming only ZFC? Here
![]() $r>1$
.
$r>1$
.
Note that all our examples of r-Ramsey and not
![]() $(r+1)$
-Ramsey spaces (which required CH) are Fréchet–Urysohn, but the ZFC example that was not
$(r+1)$
-Ramsey spaces (which required CH) are Fréchet–Urysohn, but the ZFC example that was not
![]() $2$
-Ramsey, being a
$2$
-Ramsey, being a
![]() $K(\mathcal {A})$
where
$K(\mathcal {A})$
where
![]() $\mathcal {A}$
is mad, is not Fréchet–Urysohn. However, a similar example could be constructed from a completely separable mad family. The main idea is to start with a completely separable mad family on
$\mathcal {A}$
is mad, is not Fréchet–Urysohn. However, a similar example could be constructed from a completely separable mad family. The main idea is to start with a completely separable mad family on
![]() $\omega \times \omega $
as in the construction of Example 4.1. Then, deleting an infinite set from each
$\omega \times \omega $
as in the construction of Example 4.1. Then, deleting an infinite set from each
![]() $A\in \mathcal {A}$
other than the fixed columns
$A\in \mathcal {A}$
other than the fixed columns
![]() $\{n\}\times \omega $
will still give an example that fails to be
$\{n\}\times \omega $
will still give an example that fails to be
![]() $2$
-Ramsey, but it will be Fréchet–Urysohn because it is nowhere mad (see [Reference Hrušak, Hart, van Mill and Simon4] for the definitions of completely separable and nowhere mad). So we have the following example.
$2$
-Ramsey, but it will be Fréchet–Urysohn because it is nowhere mad (see [Reference Hrušak, Hart, van Mill and Simon4] for the definitions of completely separable and nowhere mad). So we have the following example.
Example 5.1 Assuming the existence of a completely separable mad family, there is an almost disjoint
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $K(\mathcal {A})$
is Fréchet–Urysohn and not
$K(\mathcal {A})$
is Fréchet–Urysohn and not
![]() $2$
-Ramsey.
$2$
-Ramsey.
Although the existence of a completely separable mad family is a relatively weak one (e.g., it follows from
![]() ${\mathfrak c}<\aleph _\omega $
or
${\mathfrak c}<\aleph _\omega $
or
![]() ${\mathfrak s}\leq {\mathfrak a}$
; see [Reference Hrušak, Hart, van Mill and Simon4]), we ask the following question.
${\mathfrak s}\leq {\mathfrak a}$
; see [Reference Hrušak, Hart, van Mill and Simon4]), we ask the following question.
Question 2 Does there exist a ZFC example of a Fréchet–Urysohn compact space without the Ramsey property?
We know that a product of any countable family of r-Ramsey spaces is r-Ramsey, and we have characterized when
![]() $2^\kappa $
is r-Ramsey. Moreover,
$2^\kappa $
is r-Ramsey. Moreover,
![]() ${\mathfrak h}$
is the minimal
${\mathfrak h}$
is the minimal
![]() $\kappa $
such that a product of fewer than
$\kappa $
such that a product of fewer than
![]() $\kappa $
many sequentially compact spaces is sequentially compact [Reference Simon6], and we conjecture the same holds for r-Ramsey. The cardinal
$\kappa $
many sequentially compact spaces is sequentially compact [Reference Simon6], and we conjecture the same holds for r-Ramsey. The cardinal
![]() ${\mathfrak h}$
has many equivalent formulations, but the one most relevant here is that
${\mathfrak h}$
has many equivalent formulations, but the one most relevant here is that
![]() $\mathfrak {h}$
is the minimal cardinality of a collection
$\mathfrak {h}$
is the minimal cardinality of a collection
![]() $\mathcal F$
of mad families on
$\mathcal F$
of mad families on
![]() $\omega $
, so that any infinite
$\omega $
, so that any infinite
![]() $X\subseteq \omega $
has infinite intersection with at least two elements of some family from
$X\subseteq \omega $
has infinite intersection with at least two elements of some family from
![]() $\mathcal {F}$
(see [Reference Blass, Foreman and Kanamori1]). This characterization also makes clear that
$\mathcal {F}$
(see [Reference Blass, Foreman and Kanamori1]). This characterization also makes clear that
![]() $\mathfrak {h}\leq \mathfrak {par}_2$
.
$\mathfrak {h}\leq \mathfrak {par}_2$
.
The proof that the product of fewer than
![]() ${\mathfrak h}$
sequentially compact spaces is sequentially compact also shows the same for r-Ramsey, but the family of sequentially compact spaces whose product is not sequentially compact given in [Reference Simon6] are, in fact, Alexandrov–Urysohn compacta over mad families, and, as we have seen, these spaces are not even
${\mathfrak h}$
sequentially compact spaces is sequentially compact also shows the same for r-Ramsey, but the family of sequentially compact spaces whose product is not sequentially compact given in [Reference Simon6] are, in fact, Alexandrov–Urysohn compacta over mad families, and, as we have seen, these spaces are not even
![]() $2$
-Ramsey. Therefore, if
$2$
-Ramsey. Therefore, if
![]() $\mu $
is the minimal cardinal for productivity of the class of
$\mu $
is the minimal cardinal for productivity of the class of
![]() $2$
-Ramsey spaces, then
$2$
-Ramsey spaces, then
![]() $\mathfrak {h}\leq \mu $
and we conjecture that
$\mathfrak {h}\leq \mu $
and we conjecture that
![]() $\mu =\mathfrak {h}$
.
$\mu =\mathfrak {h}$
.
Question 3 Characterize the minimal cardinal
![]() $\kappa $
satisfying the product of fewer than
$\kappa $
satisfying the product of fewer than
![]() $\kappa $
many r-Ramsey spaces is always r-Ramsey.
$\kappa $
many r-Ramsey spaces is always r-Ramsey.
Acknowledgment
The first author would like to thank Henryk Michalewski for bringing this topic and in particular for pointing out reference [Reference Bojańczyk, Kopczyński and Toruńczyk2]. The second author would like to thank the first author and the Institute of Mathematics of the Czech Academy of Sciences for support during his visit when this research was conducted.