No CrossRef data available.
Article contents
On generation of the coefficient field of a primitive Hilbert modular form by a single Fourier coefficient
Published online by Cambridge University Press: 08 September 2022
Abstract
Let f be a primitive Hilbert modular form over F of weight k with coefficient field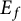
$E_f$
, generated by the Fourier coefficients
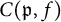$C(\mathfrak {p}, f)$
for
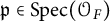$\mathfrak {p} \in \mathrm {Spec}(\mathcal {O}_F)$
. Under certain assumptions on the image of the residual Galois representations attached to f, we calculate the Dirichlet density of
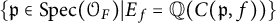$\{\mathfrak {p} \in \mathrm {Spec}(\mathcal {O}_F)| E_f = \mathbb {Q}(C(\mathfrak {p}, f))\}$
. For
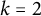$k=2$
, we show that those assumptions are satisfied when
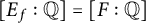$[E_f:\mathbb {Q}] = [F:\mathbb {Q}]$
is an odd prime. We also study analogous results for
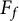$F_f$
, the fixed field of
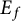$E_f$
by the set of all inner twists of f. Then, we provide some examples of f to support our results. Finally, we compute the density of
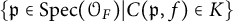$\{\mathfrak {p} \in \mathrm {Spec}(\mathcal {O}_F)| C(\mathfrak {p}, f) \in K\}$
for fields K with
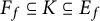$F_f \subseteq K \subseteq E_f$
.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Barnet-Lamb, T., Gee, T., and Geraghty, D., The Sato–Tate conjecture for Hilbert modular forms. J. Amer. Math. Soc. 24(2011), no. 2, 411–469.CrossRefGoogle Scholar
Carayol, H., Sur les représentations
$l$
-adiques associées aux formes modulaires de Hilbert (in French) [On
$l$
-adic representations associated with Hilbert modular forms]. Ann. Sci. École Norm. Supér. (4) 19(1986), no. 3, 409–468.CrossRefGoogle Scholar
$l$
-adiques associées aux formes modulaires de Hilbert (in French) [On
$l$
-adic representations associated with Hilbert modular forms]. Ann. Sci. École Norm. Supér. (4) 19(1986), no. 3, 409–468.CrossRefGoogle ScholarDalal, T. and Kumar, N., On non-vanishing and sign changes of the Fourier coefficients of Hilbert cusp forms. Topics in number theory. Ramanujan Math. Soc. Lect. Notes Ser. 26(2020), 175–188.Google Scholar
Dieulefait, L. and Dimitrov, M., Explicit determination of images of Galois representations attached to Hilbert modular forms. J. Number Theory 117(2006), 397–405.CrossRefGoogle Scholar
Dimitrov, M., Galois representations modulo p and cohomology of Hilbert modular varieties. Ann. Sci. École Norm. Supér. (4) 38(2005), no. 4, 505–551.10.1016/j.ansens.2005.03.005CrossRefGoogle Scholar
Koo, K. T.-L., Stein, W., and Wiese, G., On the generation of the coefficient field of a newform by a single Hecke eigenvalue. J. Theor. Nombres Bordeaux 20(2008), no. 2, 373–384.CrossRefGoogle Scholar
Marcus, D. A., Number fields, Universitext, Springer, New York–Heidelberg, 1977.CrossRefGoogle Scholar
Ribet, K. A., On l-adic representations attached to modular forms. II. Glasg. Math. J. 27(1985), 185–194.CrossRefGoogle Scholar
Serre, J.-P., Quelques applications du théorème de densité de Chebotarev (in French) [ Some applications of the Chebotarev density theorem ]. Publ. Math. Inst. Hautes Etudes Sci. 54(1981), 323–401.CrossRefGoogle Scholar
Shemanske, T. R. and Walling, L. H., Twists of Hilbert modular forms. Trans. Amer. Math. Soc. 338(1993), no. 1, 375–403.CrossRefGoogle Scholar
Shimura, G., The special values of the zeta functions associated with Hilbert modular forms. Duke Math. J. 45(1978), no. 3, 637–679.CrossRefGoogle Scholar
Taylor, R., On Galois representations associated to Hilbert modular forms. Invent. Math. 98(1989), no. 2, 265–280.CrossRefGoogle Scholar
The LMFDB Collaboration, The L-functions and Modular Forms Database, 2021. http://www.lmfdb.org [accessed September 7, 2022].Google Scholar