Article contents
On Identities with Composition of Generalized Derivations
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $R$ be a prime ring with extended centroid
$R$ be a prime ring with extended centroid 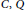 $\text{C,Q}$ maximal right ring of quotients of
$\text{C,Q}$ maximal right ring of quotients of  $R$ ,
$R$ , 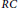 $RC$ central closure of
$RC$ central closure of  $R$ such that
$R$ such that 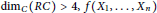 ${{\dim}_{C}}(RC)>4,f({{X}_{1}},...,{{X}_{n}})$ a multilinear polynomial over
${{\dim}_{C}}(RC)>4,f({{X}_{1}},...,{{X}_{n}})$ a multilinear polynomial over  $C$ that is not central-valued on
$C$ that is not central-valued on  $R$ , and
$R$ , and 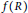 $f(R)$ the set of all evaluations of the multilinear polynomial
$f(R)$ the set of all evaluations of the multilinear polynomial 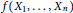 $f({{X}_{1}},...,{{X}_{n}})$ in
$f({{X}_{1}},...,{{X}_{n}})$ in  $R$ . Suppose that
$R$ . Suppose that 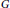 $G$ is a nonzero generalized derivation of
$G$ is a nonzero generalized derivation of  $R$ such that
$R$ such that 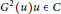 ${{G}^{2}}(u)u\in C$ for all
${{G}^{2}}(u)u\in C$ for all 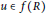 $u\in f(R)$ . Then one of the following conditions holds:
$u\in f(R)$ . Then one of the following conditions holds:
-
(i) there exists
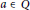 $a\in \text{Q}$ such that
$a\in \text{Q}$ such that 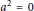 ${{a}^{2}}=0$ and either
${{a}^{2}}=0$ and either 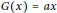 $G(x)=ax$ for all
$G(x)=ax$ for all  $x\in R$ or
$x\in R$ or 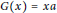 $G(x)=xa$ for all
$G(x)=xa$ for all  $x\in R$ ;
$x\in R$ ; -
(ii) there exists
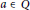 $a\in \text{Q}$ such that
$a\in \text{Q}$ such that 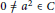 $0\ne {{a}^{2}}\in C$ and either
$0\ne {{a}^{2}}\in C$ and either 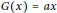 $G(x)=ax$ for all
$G(x)=ax$ for all  $x\in R$ or
$x\in R$ or 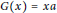 $G(x)=xa$ for all
$G(x)=xa$ for all  $x\in R$ and
$x\in R$ and 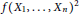 $f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$ is central-valued on
$f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$ is central-valued on  $R$ ;
$R$ ; -
(iii) char
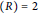 $(R)=2$ and one of the following holds:
$(R)=2$ and one of the following holds:
-
(a) there exist
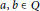 $a,b,\in \text{Q}$ such that
$a,b,\in \text{Q}$ such that 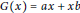 $G(x)=ax+xb$ for all
$G(x)=ax+xb$ for all  $x\in R$ and
$x\in R$ and  ${{a}^{2}}={{b}^{2}}\in C$ ;
${{a}^{2}}={{b}^{2}}\in C$ ; -
(b) there exist
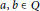 $a,b,\in \text{Q}$ such that
$a,b,\in \text{Q}$ such that 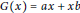 $G(x)=ax+xb$ for all
$G(x)=ax+xb$ for all 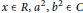 $x\in R,\,{{a}^{2}},{{b}^{2}}\in C$ and
$x\in R,\,{{a}^{2}},{{b}^{2}}\in C$ and 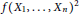 $f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$ is central-valued on
$f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$ is central-valued on  $R$ ;
$R$ ; -
(c) there exist
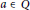 $a\in \text{Q}$ and an
$a\in \text{Q}$ and an  $X$ -outer derivation
$X$ -outer derivation  $d$ of
$d$ of  $R$ such that
$R$ such that 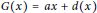 $G(x)=ax+d(x)$ for all
$G(x)=ax+d(x)$ for all 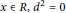 $x\in R,{{d}^{2}}=0$ and
$x\in R,{{d}^{2}}=0$ and 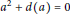 ${{a}^{2}}+d(a)=0$ ;
${{a}^{2}}+d(a)=0$ ; -
(d) there exist
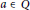 $a\in \text{Q}$ and an
$a\in \text{Q}$ and an  $X$ -outer derivation
$X$ -outer derivation  $d$ of
$d$ of  $R$ such that
$R$ such that 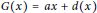 $G(x)=ax+d(x)$ for all
$G(x)=ax+d(x)$ for all 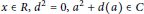 $x\in R,\,{{d}^{2}}=0,\,{{a}^{2}}+d(a)\in C$ and
$x\in R,\,{{d}^{2}}=0,\,{{a}^{2}}+d(a)\in C$ and 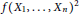 $f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$ is central-valued on
$f{{({{X}_{1}},...,{{X}_{n}})}^{2}}$ is central-valued on  $R$ .
$R$ .
Moreover, we characterize the form of nonzero generalized derivations 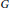 $G$ of
$G$ of  $R$ satisfying
$R$ satisfying 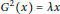 ${{G}^{2}}(x)=\lambda x$ for all
${{G}^{2}}(x)=\lambda x$ for all  $x\in R$ , where
$x\in R$ , where 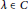 $\lambda \in C$ .
$\lambda \in C$ .
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 8
- Cited by

