Hostname: page-component-cb9f654ff-kl2l2 Total loading time: 0 Render date: 2025-08-19T20:50:17.907Z Has data issue: false hasContentIssue false
  • English
  • Français

On Minimal and Maximal p-operator Space Structures

Published online by Cambridge University Press:  20 November 2018

Serap Öztop  and
Nico Spronk
Serap Öztop
Affiliation:
Istanbul University, Faculty of Science, Department of Mathematics, 34134 Vezneciler, Istanbul, Turkey e-mail: oztops@istanbul.edu.tr
Nico Spronk
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON N2L 3G1 e-mail: nspronk@uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

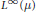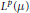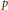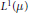We show that ${{L}^{\infty }}\left( \mu\right)$ , in its capacity as multiplication operators on ${{L}^{p}}\left( \mu\right)$ , is minimal as a $p$ -operator space for a decomposable measure $\mu $ . We conclude that ${{L}^{1}}\left( \mu\right)$ has a certain maximal type 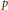$p$ -operator space structure that facilitates computations with 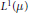${{L}^{1}}\left( \mu\right)$ and the projective tensor product.

Keywords

46L0747L2546G10p-operator spacemin spacemax space

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 166 - 177
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] An, G., Lee, J.-J., and Ruan, Z.-J., On p-approximation properties for p-operator spaces. J. Funct. Anal. 259 (2010), no. 4, 933–974. http://dx.doi.org/10.1016/j.jfa.2010.04.007 Google Scholar
[2] Blecher, D. P., The standard dual of an operator space. Pacific J. Math. 153 (1992), 15–30.Google Scholar
[3] Blecher, D. P. and Paulsen, V. I., Tensor products of operator spaces. J. Funct. Anal. 99 (1991), no. 2, 262–292. http://dx.doi.org/10.1016/0022-123691)90042-4 Google Scholar
[4] Davidson, K. R., C*-algebras by example. Fields Institute Monographs, 6, American Mathematical Society, Providence, RI, 1996.Google Scholar
[5] Daws, M., p-operator spaces and Fig`a-Talamanca–Herz algebras. J. Operator Theory 63 (2010), no. 1, 41–83.Google Scholar
[6] Diestel, J. and Uhl, J. J. Jr., Vector measures. Mathematical Surveys, 15, American Mathematical Society, Providence, RI, 1977.Google Scholar
[7] Effros, E. G. and Ruan, Z.-J., On matricially normed spaces. Pacific J. Math. 132 (1988), no. 2, 243–264.Google Scholar
[8] Effros, E. G. and Ruan, Z.-J., Operator spaces. London Mathematical Society Monographs. New Series, 23, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[9] Folland, G. B., Real analysis., Modern techniques and their applications. Second ed., Pure and Applied Mathematics,Wiley-Interscience, New York, 1999.Google Scholar
[10] Junge, M., Factorization theory for spaces of operators. Habilitationschrift, Christian-Albrechts-Universität zu Kiel, 1996.Google Scholar
[11] Lee, J.-J., On p-operator spaces and their applications. Ph.D. Thesis, University of Illinois at Urbana-Champaign, ProQuest LLC, Ann Arbor, MI, 2010.Google Scholar
[12] Le Merdy, C., Factorization of p-completely bounded multilinear maps. Pacific J. Math. 172 (1995), no. 1, 187–213.Google Scholar
[13] Pisier, G., Completely bounded maps between sets of Banach space operators. Indiana Univ. Math. J. 39 (1990), no. 1, 249–277. http://dx.doi.org/10.1512/iumj.1990.39.39014 Google Scholar
[14] Ryan, R. A., Introduction to tensor products of Banach spaces. Springer Monographs in Mathematics, Springer, New York, 2002.Google Scholar
[15] Singer, I., Linear functionals on the space of continuous mappings of a compact Hausdorff space into aBanach space. (Russian) Rev. Math. Pures Appl. 2 (1957), 301–315.Google Scholar
[16] Singer, I., Les duals de certains espaces de Banach de champs de vecteurs. II. Bull. Sci. Math. (2) 83 (1959), 73–96.Google Scholar