Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shaveisi, Farzad
2016.
Some Results on Annihilating-ideal Graphs.
Canadian Mathematical Bulletin,
Vol. 59,
Issue. 3,
p.
641.
Akbari, Saeeid
Alilou, Abbas
Amjadi, Jafar
and
Mahmoud Sheikholeslami, Seyed
2017.
The Co-annihilating-ideal Graphs of Commutative Rings.
Canadian Mathematical Bulletin,
Vol. 60,
Issue. 1,
p.
3.
Bagheri, Saeid
Nabaei, Fatemeh
Rezaeii, Rashid
and
Samei, Karim
2018.
Reduction graph and its application on algebraic graphs.
Rocky Mountain Journal of Mathematics,
Vol. 48,
Issue. 3,
Visweswaran, S.
and
Parejiya, Jaydeep
2018.
Some results on the complement of the comaximal ideal graphs of commutative rings.
Ricerche di Matematica,
Vol. 67,
Issue. 2,
p.
709.
VİSWESWARAN, Subramanian
and
PAREJİYA, Jaydeep
2018.
Some results on the comaximal ideal graph of a commutative ring.
Journal of Algebra Combinatorics Discrete Structures and Applications,
Vol. 5,
Issue. 2,
p.
85.
Shen, Shouqiang
Liu, Weijun
and
Feng, Lihua
2018.
Some properties of comaximal right ideal graph of a ring.
Applied Mathematics and Computation,
Vol. 333,
Issue. ,
p.
225.
Selvakumar, K.
and
Amritha, V. C.
2019.
On the genus of the k-maximal hypergraph of commutative rings.
Discrete Mathematics, Algorithms and Applications,
Vol. 11,
Issue. 01,
p.
1950010.
Parejiya, Jaydeep
Sarman, Patat
and
Vadhel, Pravin
2020.
Planarity of a unit graph: Part-I local case.
Malaya Journal of Matematik,
Vol. 8,
Issue. 3,
p.
1155.
Parejiya, Jaydeep
Sarman, Patat
and
Vadhel, Pravin
2020.
Planarity of a unit graph part -III $ |Max(R)| \geq 3 $ case.
Malaya Journal of Matematik,
Vol. 8,
Issue. 4,
p.
1413.
Esmaili, Kyuoomars
and
Samei, Karim
2021.
Cut vertices in comaximal graph of a commutative Artinian ring.
Indian Journal of Pure and Applied Mathematics,
Vol. 52,
Issue. 2,
p.
340.
Amritha, V. C.
and
Selvakumar, K.
2022.
Ideal based hypergraph of a commutative ring.
AKCE International Journal of Graphs and Combinatorics,
Vol. 19,
Issue. 1,
p.
18.
Banerjee, Subarsha
2022.
Laplacian spectrum of comaximal graph of the ring ℤ
n
.
Special Matrices,
Vol. 10,
Issue. 1,
p.
285.
Banerjee, Subarsha
2022.
Spectra and Topological Indices of Comaximal Graph of $${\mathbb {Z}}_{n}$$.
Results in Mathematics,
Vol. 77,
Issue. 3,
Banerjee, Subarsha
2023.
The adjacency spectrum and metric dimension of an induced subgraph of comaximal graph of ℤn.
Discrete Mathematics, Algorithms and Applications,
Vol. 15,
Issue. 03,
Shoar, Hanieh
Salimi, Maryam
Tehranian, Abolfazl
Rasouli, Hamid
and
Tavasoli, Elham
2023.
Comaximal graph of amalgamated algebras along an ideal.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 01,
Rather, Bilal Ahmad
Diene, Adama
and
Imran, Muhammad
2024.
Linear strand of edge ideals of comaximal graphs of commutative rings.
Communications in Algebra,
Vol. 52,
Issue. 4,
p.
1486.
Rather, Bilal Ahmad
Imran, Muhammed
and
Pirzada, S.
2024.
Sombor index and eigenvalues of comaximal graphs of commutative rings.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 06,
Ballal, Sachin
Puranik, Sadashiv
and
Kharat, Vilas
2024.
A note on comaximal graph and maximal topology on multiplication le-modules.
Quasigroups and Related Systems,
Vol. 31,
Issue. 2(50),
p.
175.
Su, Huadong
and
Huang, Chunhong
2024.
Finite commutative rings whose line graphs of comaximal graphs have genus at most two.
Hacettepe Journal of Mathematics and Statistics,
Vol. 53,
Issue. 4,
p.
1075.
Rather, Bilal Ahmad
Aouchiche, Mustapha
and
Imran, Muhammed
2024.
On Laplacian integrability of comaximal graphs of commutative rings.
Indian Journal of Pure and Applied Mathematics,
Vol. 55,
Issue. 1,
p.
310.
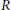 $R$ be a commutative ring with 1. In a 1995 paper in J. Algebra, Sharma and Bhatwadekar defined a graph on
$R$ be a commutative ring with 1. In a 1995 paper in J. Algebra, Sharma and Bhatwadekar defined a graph on 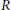 $R$ ,
$R$ , 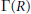 $\Gamma \left( R \right)$ , with vertices as elements of
$\Gamma \left( R \right)$ , with vertices as elements of 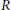 $R$ , where two distinct vertices
$R$ , where two distinct vertices  $a$ and
$a$ and 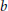 $b$ are adjacent if and only if
$b$ are adjacent if and only if 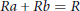 $Ra\,+\,Rb\,=\,R$ . In this paper, we consider a subgraph
$Ra\,+\,Rb\,=\,R$ . In this paper, we consider a subgraph 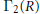 ${{\Gamma }_{2}}\left( R \right)$ of
${{\Gamma }_{2}}\left( R \right)$ of 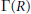 $\Gamma \left( R \right)$ that consists of non-unit elements. We investigate the behavior of
$\Gamma \left( R \right)$ that consists of non-unit elements. We investigate the behavior of 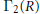 ${{\Gamma }_{2}}\left( R \right)$ and
${{\Gamma }_{2}}\left( R \right)$ and 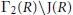 ${{\Gamma }_{2}}\left( R \right)\backslash \text{J}\left( R \right)$ , where
${{\Gamma }_{2}}\left( R \right)\backslash \text{J}\left( R \right)$ , where 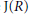 $\text{J}\left( R \right)$ is the Jacobson radical of
$\text{J}\left( R \right)$ is the Jacobson radical of 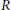 $R$ . We associate the ring properties of
$R$ . We associate the ring properties of 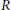 $R$ , the graph properties of
$R$ , the graph properties of 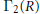 ${{\Gamma }_{2}}\left( R \right)$ , and the topological properties of
${{\Gamma }_{2}}\left( R \right)$ , and the topological properties of 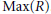 $\text{Max}\left( R \right)$ . Diameter, girth, cycles and dominating sets are investigated, and algebraic and topological characterizations are given for graphical properties of these graphs.
$\text{Max}\left( R \right)$ . Diameter, girth, cycles and dominating sets are investigated, and algebraic and topological characterizations are given for graphical properties of these graphs.
