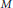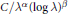Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mangoubi, Dan
2008.
Local Asymmetry and the Inner Radius of Nodal Domains.
Communications in Partial Differential Equations,
Vol. 33,
Issue. 9,
p.
1611.
MANGOUBI, DAN
2010.
THE VOLUME OF A LOCAL NODAL DOMAIN.
Journal of Topology and Analysis,
Vol. 02,
Issue. 02,
p.
259.
Samajdar, Rhine
and
Jain, Sudhir R.
2014.
A nodal domain theorem for integrable billiards in two dimensions.
Annals of Physics,
Vol. 351,
Issue. ,
p.
1.
Band, Ram
and
Fajman, David
2016.
Topological Properties of Neumann Domains.
Annales Henri Poincaré,
Vol. 17,
Issue. 9,
p.
2379.
Jain, Sudhir Ranjan
and
Samajdar, Rhine
2017.
Nodal portraits of quantum billiards: Domains, lines, and statistics.
Reviews of Modern Physics,
Vol. 89,
Issue. 4,
Georgiev, Bogdan
and
Mukherjee, Mayukh
2018.
Nodal geometry, heat diffusion and Brownian motion.
Analysis & PDE,
Vol. 11,
Issue. 1,
p.
133.
Georgiev, Bogdan
2019.
On the Lower Bound of the Inner Radius of Nodal Domains.
The Journal of Geometric Analysis,
Vol. 29,
Issue. 2,
p.
1546.
Georgiev, Bogdan
and
Mukherjee, Mayukh
2019.
Some remarks on nodal geometry in the smooth setting.
Calculus of Variations and Partial Differential Equations,
Vol. 58,
Issue. 3,
Decio, Stefano
2022.
Nodal Sets of Steklov Eigenfunctions near the Boundary: Inner Radius Estimates.
International Mathematics Research Notices,
Vol. 2022,
Issue. 21,
p.
16709.
Mukherjee, Mayukh
and
Saha, Soumyajit
2022.
Nodal sets of Laplace eigenfunctions under small perturbations.
Mathematische Annalen,
Vol. 383,
Issue. 1-2,
p.
475.
Georgiev, Bogdan
and
Mukherjee, Mayukh
2022.
Some applications of heat flow to Laplace eigenfunctions.
Communications in Partial Differential Equations,
Vol. 47,
Issue. 4,
p.
677.
Charron, Philippe
and
Mangoubi, Dan
2024.
The inner radius of nodal domains in high dimensions.
Advances in Mathematics,
Vol. 452,
Issue. ,
p.
109787.