Let 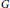$G$ be a graph and let $\tau $ be an assignment of nonnegative integer thresholds to the vertices of 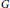$G$ . A subset of vertices, 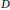$D$ , is said to be a $\tau $ -dynamicmonopoly if 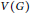$V\left( G \right)$ can be partitioned into subsets 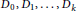${{D}_{0}},\,{{D}_{1}},\,\ldots \,,\,{{D}_{k}}$ such that 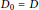${{D}_{0}}\,=\,D$ and for any 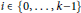$i\,\in \,\left\{ 0,\,\ldots \,,\,k-1 \right\}$ , each vertex $v$ in 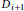${{D}_{i+1}}$ has at least 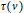$\tau \left( v \right)$ neighbors in 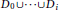${{D}_{0}}\cup \cdots \cup {{D}_{i}}$ . Denote the size of smallest $\tau $ -dynamic monopoly by 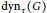$\text{dy}{{\text{n}}_{\tau }}\left( G \right)$ and the average of thresholds in $\tau $ by $\bar{\tau }$ . We show that the values of 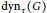$\text{dy}{{\text{n}}_{\tau }}\left( G \right)$ over all assignments $\tau $ with the same average threshold is a continuous set of integers. For any positive number 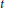$t$ , denote the maximum 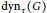$\text{dy}{{\text{n}}_{\tau }}\left( G \right)$ taken over all threshold assignments $\tau $ with 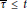$\bar{\tau }\,\le \,t$ , by 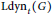$\text{Ldy}{{\text{n}}_{t}}\left( G \right)$ . In fact, 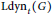$\text{Ldy}{{\text{n}}_{t}}\left( G \right)$ shows the worst-case value of a dynamicmonopoly when the average threshold is a given number 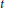$t$ . We investigate under what conditions on 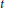$t$ , there exists an upper bound for 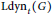$\text{Ldy}{{\text{n}}_{t}}\left( G \right)$ of the form 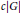$c\left| G \right|$ , where 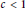$c\,<\,1$ . Next, we show that 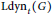$\text{Ldy}{{\text{n}}_{t}}\left( G \right)$ is 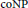$\text{coNP}$ -hard for planar graphs but has polynomial-time solution for forests.