Article contents
On the Number of Divisors of the Quadratic Form m2 + n2
Published online by Cambridge University Press: 20 November 2018
Abstract
For an integer 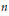 $n$ , let
$n$ , let 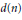 $d\left( n \right)$ denote the ordinary divisor function. This paper studies the asymptotic behavior of the sum
$d\left( n \right)$ denote the ordinary divisor function. This paper studies the asymptotic behavior of the sum
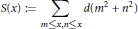 $$S\left( x \right)\,:=\sum\limits_{m\le x,n\le x}{d\left( {{m}^{2}}+{{n}^{2}} \right)}$$
$$S\left( x \right)\,:=\sum\limits_{m\le x,n\le x}{d\left( {{m}^{2}}+{{n}^{2}} \right)}$$
It is proved in the paper that, as 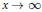 $x\,\to \,\infty $ ,
$x\,\to \,\infty $ ,
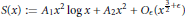 $$S(x):={{A}_{1}}{{x}^{2}}\log x+{{A}_{2}}{{x}^{2}}+{{O}_{\in }}({{x}^{\frac{3}{2}+\in }}),$$
$$S(x):={{A}_{1}}{{x}^{2}}\log x+{{A}_{2}}{{x}^{2}}+{{O}_{\in }}({{x}^{\frac{3}{2}+\in }}),$$
where 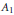 ${{A}_{1}}$ and
${{A}_{1}}$ and 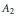 ${{A}_{2}}$ are certain constants and
${{A}_{2}}$ are certain constants and 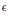 $\in $ is any fixed positive real number.
$\in $ is any fixed positive real number.
The result corrects a false formula given in a paper of Gafurov concerning the same problem, and improves the error 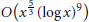 $O({{x}^{\frac{5}{3}}}\,{{(\log \,x)}^{9}})$ claimed by Gafurov.
$O({{x}^{\frac{5}{3}}}\,{{(\log \,x)}^{9}})$ claimed by Gafurov.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
- 10
- Cited by

