Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-31T03:55:13.101Z Has data issue: false hasContentIssue false
  • English
  • Français

On the sign changes of Dirichlet coefficients of triple product L-functions

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  14 November 2024

Jinzhi Feng
Jinzhi Feng*
Affiliation:
School of Mathematics, Shandong University, Jinan 250100, China
*
e-mail: fengjinzhi@mail.sdu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let f and g be two distinct normalized primitive holomorphic cusp forms of even integral weight 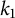$k_{1}$ and 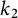$k_{2}$ for the full modular group 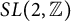$SL(2,\mathbb {Z})$, respectively. Suppose that 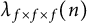$\lambda _{f\times f\times f}(n)$ and 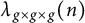$\lambda _{g\times g\times g}(n)$ are the n-th Dirichlet coefficient of the triple product L-functions 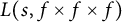$L(s,f\times f\times f)$ and 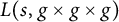$L(s,g\times g\times g)$. In this paper, we consider the sign changes of the sequence 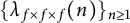$\{\lambda _{f\times f\times f}(n)\}_{n\geq 1}$ and 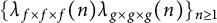$\{\lambda _{f\times f\times f}(n)\lambda _{g\times g\times g}(n)\}_{n\geq 1}$ in short intervals and establish quantitative results for the number of sign changes for 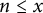$n \leq x$, which improve the previous results.

Keywords

sign changeDirichlet coefficientcusp form

MSC classification

Primary: 11F11: Holomorphic modular forms of integral weight
Secondary: 11F30: Fourier coefficients of automorphic forms 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 4 , December 2024 , pp. 1092 - 1106
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Deligne, P., La conjecture de Weil. I . Inst. Hautes Études Sci. Publ. Math. 43(1974), no. 43, 273–307. MR 340258CrossRefGoogle Scholar
Garrett, P. B., Decomposition of Eisenstein series: Rankin triple products . Ann. of Math. (2) 125(1987), no. 2, 209–235. MR 881269CrossRefGoogle Scholar
Gun, S., Kumar, B. and Paul, B., The first simultaneous sign change and non-vanishing of Hecke eigenvalues of newforms . J. Number Theory 200(2019), 161–184. MR 3944435CrossRefGoogle Scholar
Heath-Brown, D. R., A new $kth$ derivative estimate for a trigonometric sum via Vinogradov’s integral. Tr. Mat. Inst. Steklova 296(2017), 95–110, English version published in Proc. Steklov Inst. Math. 296(2017), no. 1, 88–103.Google Scholar
Hua, G., On the simultaneous sign changes of Hecke eigenvalues over an integral binary quadratic form . Acta Math. Hungar. 167(2022), no. 2, 476–491. MR 4487620CrossRefGoogle Scholar
Hua, G., On the simultaneous sign changes of coefficients of Rankin-Selberg L-functions over a certain integral binary quadratic form. Math. Pannon. (2023), no. 2, 244–257.CrossRefGoogle Scholar
Hua, G., On the sign changes of the coefficients attached to triple product $L$ -functions. Int. J. Number Theory 20(2024), no. 08, 2069–2081.CrossRefGoogle Scholar
Huang, J., Higher moments of automorphic $L$ -functions of $GL(r)$ and its applications. Acta Math. Hungar. 169(2023), no. 2, 489–502. MR 4594312CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications, Vol. 53, American Mathematical Society, Providence, RI, 2004.Google Scholar
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I . Amer. J. Math. 103(1981), no. 3, 499–558. MR 618323CrossRefGoogle Scholar
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I . Amer. J. Math. 103(1981), no. 3, 499–558. MR 618323CrossRefGoogle Scholar
Knopp, M., Kohnen, W. and Pribitkin, W., On the signs of fourier coefficients of cusp forms . Ramanujan J. 7(2003), no. 1, 269–277.CrossRefGoogle Scholar
Kumari, M. and Ram Murty, M., Simultaneous non-vanishing and sign changes of Fourier coefficients of modular forms . Int. J. Number Theory 14(2018), no. 8, 2291–2301. MR 3846406CrossRefGoogle Scholar
Lao, H. and Luo, S., Sign changes and nonvanishing of Fourier coefficients of holomorphic cusp forms . Rocky Mountain J. Math. 51(2021), no. 5, 1701–1714. MR 4382993CrossRefGoogle Scholar
Lau, Y.-K. and Wu, J., A density theorem on automorphic $L$ -functions and some applications. Trans. Amer. Math. Soc. 358(2006), no. 1, 441–472. MR 2171241CrossRefGoogle Scholar
Lin, Y., Nunes, R. and Qi, Z., Strong subconvexity for self-dual $GL(3)$ $L$ -functions. Int. Math. Res. Not. IMRN 2023(2023), no. 13, 11453–11470.CrossRefGoogle Scholar
Liu, H., The second moment of the Fourier coefficients of triple product $L$ -functions. Proc. Indian Acad. Sci. Math. Sci. 133(2023), no. 1, Paper No. 8, 12. MR 4572184CrossRefGoogle Scholar
Lü, G. and Sankaranarayanan, A., On the coefficients of triple product $L$ -functions. Rocky Mountain J. Math. 47(2017), no. 2, 553–570. MR 3635374CrossRefGoogle Scholar
Meher, J., Shankhadhar, K. D. and Viswanadham, G. K., A short note on sign changes . Proc. Indian Acad. Sci. Math. Sci. 123(2013), no. 3, 315–320. MR 3102375CrossRefGoogle Scholar
Ram Murty, M., Oscillations of Fourier coefficients of modular forms . Math. Ann. 262(1983), no. 4, 431–446. MR 696516CrossRefGoogle Scholar
Newton, J. and Thorne, J. A., Symmetric power functoriality for holomorphic modular forms . Publ. Math. Inst. Hautes Études Sci. 134(2021), 1–116. MR 4349240CrossRefGoogle Scholar
Newton, J. and Thorne, J. A., Symmetric power functoriality for holomorphic modular forms, II . Publ. Math. Inst. Hautes Études Sci. 134(2021), 117–152. MR 4349241CrossRefGoogle Scholar
Perelli, A., General $L$ -functions. Ann. Mat. Pura Appl. 130(1982), 287–306.CrossRefGoogle Scholar
Piatetski-Shapiro, I. and Rallis, S., Rankin triple $L$ functions. Compos. Math. 64(1987), no. 1, 31–115.Google Scholar
Rudnick, Z. and Sarnak, P., Zeros of principal $L$ -functions and random matrix theory. Duke Math. J. 81(1996), no. 2, 269–322 (English).CrossRefGoogle Scholar
Shahidi, F., On certain $L$ -functions. Amer. J. Math. 103(1981), no. 2, 297–355. MR 610479CrossRefGoogle Scholar
Shahidi, F., Third symmetric power $L$ -functions for GL(2). Compos. Math. 70(1989), no. 3, 245–273. MR 1002045Google Scholar