Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-23T14:15:33.671Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Structure of Cuntz Semigroups in (Possibly) Nonunital C*-algebras

Published online by Cambridge University Press:  20 November 2018

Aaron Peter Tikuisis  and
Andrew Toms
Aaron Peter Tikuisis
Affiliation:
Institute of Mathematics, University of Aberdeen, Aberdeen, United Kingdom. e-mail: a.tikuisis@abdn.ac.uk
Andrew Toms
Affiliation:
Department of Mathematics, Purdue University, 150 North University Street, West Lafayette, IN 47907, USA. e-mail: atoms@purdue.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We examine the ranks of operators in semi-finite 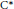${{C}^{*}}$-algebras as measured by their densely defined lower semicontinuous traces. We first prove that a unital simple 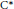${{C}^{*}}$-algebra whose extreme tracial boundary is nonempty and finite contains positive operators of every possible rank, independent of the property of strict comparison. We then turn to nonunital simple algebras and establish criteria that imply that the Cuntz semigroup is recovered functorially from the Murray–von Neumann semigroup and the space of densely defined lower semicontinuous traces. Finally, we prove that these criteria are satisfied by not-necessarily-unital approximately subhomogeneous algebras of slow dimension growth. Combined with results of the first author, this shows that slow dimension growth coincides with $Z$-stability for approximately subhomogeneous algebras.

Keywords

46L3546L0546L8047L4046L85Nuclear C*-algebrasCuntz semigroupdimension functionsstably projectionless C*-algebrasapproximately subhomogeneous C*-algebrasslow dimension growth
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 402 - 414
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Blackadar, B. and Handelman, D., Dimension functions and traces onC* -algebras. J. Fund. Anal. 45 (1982), no. 3, 297–340. http://dx.doi.Org/10.1016/0022-1236(82)90009-X Google Scholar
[2] Blanchard, E. and Kirchberg, E., Non-simple purely infinite C* -algebras: the Hausdorff case. J. Fund. Anal. 207 (2004), no. 2, 461–513. http://dx.doi.Org/10.1016/j.jfa.2003.06.008 Google Scholar
[3] Brown, L. G., Stable isomorphism of hereditary subalgebras of C* -algebras. Pacific J. Math. 71 (1977), no. 2, 335–348. http://dx.doi.Org/10.2140/pjm.1977.71.335 Google Scholar
[4] Brown, N. P., F. Perera, and Toms, A. S., The Cuntz semigroup, the Elliott conjecture, and dimension functions on C* -algebras. J. Reine Angew. Math. 621 (2008), 191–211.Google Scholar
[5] Coward, K. T., Elliott, G. A., and Ivanescu, C., The Cuntz semigroup as an invariant for C* -algebras. J. Reine Angew. Math. 623 (2008), 161–193.Google Scholar
[6] Dadarlat, M. and Toms, A. S., Ranks of operators in simple C* -algebras. J. Fund. Anal. 259 (2010), no. 5, 1209–1229. http://dx.doi.Org/10.1016/j.jfa.2010.03.022 Google Scholar
[7] Edwards, D. A., Separation des fonctions réelles définies sur un simplexe de Choquet. C. R. Acad. Sci. Paris 261 (1965), 2798–2800.Google Scholar
[8] Elliott, G. A., Niu, Z., Santiago, L., and Tikuisis, A., Decomposition rank of approximately subhomogeneous C*-algebras. http://homepages.abdn.ac.Uk/a.tikuisis/ENST.pdfGoogle Scholar
[9] Elliott, G., Robert, L., and Santiago, L., The cone of lower semicontinuous traces on a C*-algebra. Amer. J. Math. 133 (2011), no. 4, 969–1005. http://dx.doi.Org/1O.1353/ajm.2O11.0027 Google Scholar
[10] Goodearl, K. R., Partially ordered abelian groups with interpolation. Mathematical Surveys and Monographs, 20, American Mathematical Society, Providence, RI, 1986.Google Scholar
[11] Haagerup, U., Quasi-traces on exact C*-algebras are traces. arxiv:1403.7653Google Scholar
[12] Matui, H. and Sato, Y., Strict comparison and Z-absorption of nuclear C* -algebras. Acta Math. 209 (2012), no. 1, 179–196. http://dx.doi.org/10.1007/s11511–012-0084-4 Google Scholar
[13] Pedersen, G. K., C* -algebras and their automorphism groups. London Mathematical Society Monographs, 14, Academic Press Inc. [Harcourt Brace Jovanovich Publishers], London, 1979.Google Scholar
[14] Pedersen, G. K., Measure theory for C* algebras. Math. Scand. 19 (1966), 131–145.Google Scholar
[15] Pedersen, G. K., Measure theory for C* algebras. III. Math. Scand. 25 (1969), 71–93. http://dx.doi.org/10.3891/acta.chem.scand.22–0063 Google Scholar
[16] Perera, E. and Toms, A. S., Recasting the Elliott conjecture. Math. Ann. 338 (2007), no. 3, 669–702. http://dx.doi.Org/10.1007/s00208–007-0093-3 Google Scholar
[17] Rordam, M., On the structure of simple C* -algebras tensored with a UHF-algebra. II. J. Fund. Anal. 107 (1992), no. 2, 255–269. http://dx.doi.org/10.1016/0022-1236(92)90106-S Google Scholar
[18] Rordam, M., The stable and the real rank of Z-absorbing C* -algebras. Internat. J. Math. 15 (2004), no. 10, 1065–1084. http://dx.doi.org/10.1142/S0129167X04002661 Google Scholar
[19] Tikuisis, A., Regularity for stably projectionless, simple C*-algebras. J. Fund. Anal. 263 (2012), no. 5, 1382–1407. http://dx.doi.Org/10.1016/j.jfa.2012.05.020 Google Scholar
[20] Toms, A., K-theoretic rigidity and slow dimension growth. Invent. Math. 183 (2011), no. 2, 225–244. http://dx.doi.org/10.1007/s00222-010-0273-8 Google Scholar
[21] Toms, A., Comparison theory and smooth minimal C* -dynamics. Comm. Math. Phys. 289 (2009), no. 2, 401-33. http://dx.doi.Org/10.1007/s00220–008-0665-4 Google Scholar
[22] Tikuisis, A., Nuclear dimension, Z-stability, and algebraic simplicity for stably projectionless C*-algebras. Math. Ann., to appear. http://dx.doi.Org/10.1007/s00208–013-0951-0 Google Scholar
[23] Winter, W., Nuclear dimension and Z-stability of pure C* -algebras. Invent. Math. 187 (2012), no. 2, 259–342. http://dx.doi.org/10.1007/s00222-011-0334-7 Google Scholar