Hostname: page-component-7dd5485656-bvgqh Total loading time: 0 Render date: 2025-10-31T08:50:21.549Z Has data issue: false hasContentIssue false
  • English
  • Français

Periods of Modular Forms and Imaginary Quadratic Base Change

Published online by Cambridge University Press:  20 November 2018

Mak Trifković
Mak Trifković*
Affiliation:
Mathematics and Statistics, University of Victoria, Victoria, BC, V8P 5C2 e-mail: mtrifkov@uvic.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

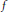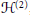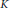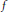Let $f$ be a classical newform of weight 2 on the upper half-plane ${{H}^{(2)}}$ , $E$ the corresponding strong Weil curve, $K$ a class number one imaginary quadratic field, and $F$ the base change of $f$ to 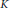$K$ . Under a mild hypothesis on the pair 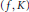$(\,f\,,\,K)$ , we prove that the period ratio 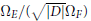${{\Omega }_{E}}/(\sqrt{\left| D \right|}{{\Omega }_{F}})$ is in 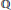$\mathbb{Q}$ . Here 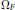${{\Omega }_{F}}$ is the unique minimal positive period of $F$ , and 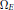${{\Omega }_{E}}$ the area of 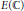$E(\mathbb{C})$ . The claim is a specialization to base change forms of a conjecture proposed and numerically verified by Cremona and Whitley.

Keywords

11F67

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 3 , 01 September 2010 , pp. 571 - 576
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Asai, T., On the Doi-Naganuma lifting associated with imaginary quadratic fields. Nagoya Math. J. 71(1978), 149–167.Google Scholar
[2] Cremona, J., Hyperbolic tessellations, modular symbols, and elliptic curves over complex quadratic fields. Compositio Math. 51(1984), no. 3, 275–324.Google Scholar
[3] Cremona, J., Abelian varieties with extra twist, cusp forms, and elliptic curves over imaginary quadratic fields. J. London Math. Soc. 45(1992), no. 3, 404–416. doi:10.1112/jlms/s2-45.3.404Google Scholar
[4] Cremona, J., and Whitley, E., Periods of cusp forms and elliptic curves over imaginary quadratic fields. Math. Comp. 62(1994), no. 205, 407–429. doi:10.2307/2153419Google Scholar
[5] Friedberg, S., On the imaginary quadratic Doi–Naganuma lifting of modular forms of arbitrary level. Nagoya Math. J. 92(1983), 1–20.Google Scholar
[6] Jacquet, H., Automorphic Forms on GL(2). Part II. Lecture Notes in Mathematics 278. Springer-Verlag, Berlin, 1972.Google Scholar
[7] Kurčanov, P., The cohomology of discrete groups and Dirichlet series that are related to Jacquet-Langlands cusp forms. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 42(1978), no. 3, 588–601.Google Scholar
[8] Mazur, B., and Swinnerton-Dyer, P., Arithmetic of Weil curves. Invent. Math. 25(1974), 1–61. doi:10.1007/BF01389997Google Scholar
[9] Miyake, T., Modular forms. Translated from the Japanese by Yoshitaka Maeda. Springer-Verlag, Berlin, 1989.Google Scholar
[10] Rohrlich, D. E., On L-functions of elliptic curves and cyclotomic towers. Invent. Math. 75(1984), no. 3, 409–423. doi:10.1007/BF01388636Google Scholar
[11] Taylor, R., l-adic representations associated to modular forms over imaginary quadratic fields. II. Invent. Math. 116(1994), no. 1-3, 619–643. doi:10.1007/BF01231575Google Scholar
[12] Trifković, M., Stark-Heegner points on elliptic curves defined over imaginary quadratic fields. Duke Math. J. 135(2006), no. 3, 415–453. doi:10.1215/S0012-7094-06-13531-7Google Scholar