In this paper, we show that the Möbius invariant function space 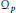${{\mathcal{Q}}_{p}}$ can be generated by variant Dirichlet type spaces ${{\mathcal{D}}_{\mu ,p}}$ induced by finite positive Borel measures $\mu $ on the open unit disk. A criterion for the equality between the space ${{\mathcal{D}}_{\mu ,p}}$ and the usual Dirichlet type space 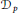${{\mathcal{D}}_{p}}$ is given. We obtain a sufficient condition to construct different ${{\mathcal{D}}_{\mu ,p}}$ spaces and provide examples. We establish decomposition theorems for ${{\mathcal{D}}_{\mu ,p}}$ spaces and prove that the non-Hilbert space 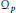${{\mathcal{Q}}_{p}}$ is equal to the intersection of Hilbert spaces ${{\mathcal{D}}_{\mu ,p}}$. As an application of the relation between 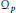${{\mathcal{Q}}_{p}}$ and ${{\mathcal{D}}_{\mu ,p}}$ spaces, we also obtain that there exist different ${{\mathcal{D}}_{\mu ,p}}$ spaces; this is a trick to prove the existence without constructing examples.