Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T03:34:23.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Real Hypersurfaces in the Complex Quadric with Lie Invariant Structure Jacobi Operator

Part of: Global differential geometry

Published online by Cambridge University Press:  10 June 2019

Young Jin Suh  and
Gyu Jong Kim
Young Jin Suh
Affiliation:
Kyungpook National University, College of Natural Sciences, Department of Mathematics, and Research Institute of Real & Complex Manifolds, Daegu41566, Republic of Korea Email: yjsuh@knu.ac.krhb2107@naver.com
Gyu Jong Kim
Affiliation:
Kyungpook National University, College of Natural Sciences, Department of Mathematics, and Research Institute of Real & Complex Manifolds, Daegu41566, Republic of Korea Email: yjsuh@knu.ac.krhb2107@naver.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notion of Lie invariant structure Jacobi operators for real hypersurfaces in the complex quadric 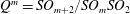$Q^{m}=SO_{m+2}/SO_{m}SO_{2}$. The existence of invariant structure Jacobi operators implies that the unit normal vector field $N$ becomes 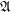$\mathfrak{A}$-principal or 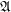$\mathfrak{A}$-isotropic. Then, according to each case, we give a complete classification of real hypersurfaces in 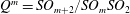$Q^{m}=SO_{m+2}/SO_{m}SO_{2}$ with Lie invariant structure Jacobi operators.

Keywords

invariant structure Jacobi operator𝔄-isotropic𝔄-principalKähler structurecomplex conjugationcomplex quadric

MSC classification

Primary: 53C40: Global submanifolds
Secondary: 53C55: Hermitian and Kählerian manifolds
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 204 - 221
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by grant Proj. No. NRF-2018-R1D1A1B-05040381 and the second by grant Proj. No. NRF-2018-R1A6A3A-01011828 from National Research Foundation of Korea. Young Jin Suh is the corresponding author.

References

Berndt, J. and Suh, Y. J., Real hypersurfaces with isometric Reeb flow in complex quadrics. Internat. J. Math. 24(2013), 1350050. https://doi.org/10.1142/S0129167X1350050X.Google Scholar
Berndt, J. and Suh, Y. J., Contact hypersurfaces in Kaehler manifold. Proc. Amer. Math. Soc. 143(2015), 2637–2649. https://doi.org/10.1090/S0002-9939-2015-12421-5.Google Scholar
Jeong, I., Kim, H. J., and Suh, Y.J., Real hypersurfaces in complex two-plane Grassmannians with parallel normal Jacobi operator. Publ. Math. Debrecen 76(2010), 203–218.Google Scholar
Klein, S., Totally geodesic submanifolds in the complex quadric. Differential Geom. Appl. 26(2008), 79–96. https://doi.org/10.1016/j.difgeo.2007.11.004.Google Scholar
Kobayashi, S. and Nomizu, K., Foundations of differential geometry. Vol. II. Wiley Classics Library, John Wiley & Sons, Inc., New York, 1996.Google Scholar
Pérez, J. D., Commutativity of Cho and structure Jacobi operators of a real hypersurface in a complex projective space. Ann. Mat. Pura Appl. 194(2015), 1781–1794. https://doi.org/10.1007/s10231-014-0444-0.Google Scholar
Pérez, J. D. and Suh, Y. J., The Ricci tensor of real hypersurfaces in complex two-plane Grassmannians. J. Korean Math. Soc. 44(2007), 211–235. https://doi.org/10.4134/JKMS.2007.44.1.211.Google Scholar
Reckziegel, H., On the geometry of the complex quadric. In: Geometry and topology of submanifolds VIII (Brussels/Nordfjordeid 1995). World Sci. Publ., River Edge, NJ, 1995, pp. 302–315.Google Scholar
Smyth, B., Differential geometry of complex hypersurfaces. Ann. of Math. 85(1967), 246–266. https://doi.org/10.2307/1970441.Google Scholar
Suh, Y. J., Real hypersurfaces of type B in complex two-plane Grassmannians. Monatsh. Math. 147(2006), 337–355. https://doi.org/10.1007/s00605-005-0329-9.Google Scholar
Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with commuting Ricci tensor. J. Geom. Phys. 60(2010), 1792–1805. https://doi.org/10.1016/j.geomphys.2010.06.007.Google Scholar
Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with parallel Ricci tensor. Proc. Royal Soc. Edinburgh Sect. A. 142(2012), 1309–1324. https://doi.org/10.1017/S0308210510001472.Google Scholar
Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with harmonic curvature. J. Math. Pures Appl. 100(2013), 16–33. https://doi.org/10.1016/j.matpur.2012.10.010.Google Scholar
Suh, Y. J., Hypersurfaces with isometric Reeb flow in complex hyperbolic two-plane Grassmannians. Adv. in Appl. Math. 50(2013), 645–659. https://doi.org/10.1016/j.aam.2013.01.001.Google Scholar
Suh, Y. J., Real hypersurfaces in the complex quadric with Reeb parallel shape operator. Internat. J. Math. 25(2014), 1450059. https://doi.org/10.1142/S0129167X14500591.Google Scholar
Suh, Y. J., Real hypersurfaces in the complex quadric with parallel Ricci tensor. Adv. Math. 281(2015), 886–905. https://doi.org/10.1016/j.aim.2015.05.012.Google Scholar
Suh, Y. J., Real hypersurfaces in the complex quadric with harmonic curvature. J. Math. Pures Appl. 106(2016), 393–410. https://doi.org/10.1016/j.matpur.2016.02.015.Google Scholar
Suh, Y. J. and Hwang, D. H., Real hypersurfaces in the complex quadric with commuting Ricci tensor. Sci. China Math. 59(2016), 2185–2198. https://doi.org/10.1007/s11425-016-0067-7.Google Scholar
Suh, Y. J. and Kim, G. J., Real hypersurfaces in the complex hyperbolic two-plane Grassmannians with Reeb invariant Ricci tensor. Differential Geom. Appl. 47(2016), 14–25. https://doi.org/10.1016/j.difgeo.2016.03.002.Google Scholar
Suh, Y. J. and Kim, G. J., Real hypersurfaces in the complex quadric with Lie invariant normal Jacobi operator. Adv. in Appl. Math. 104(2019), 117–134. https://doi.org/10.1016/j.aam.2018.12.003.Google Scholar
Suh, Y. J. and Woo, C., Real hypersurfaces in complex hyperbolic two-plane Grassmannians with parallel Ricci tensor. Math. Nachr. 55(2014), 1524–1529. https://doi.org/10.1002/mana.201300283.Google Scholar