No CrossRef data available.
Article contents
Restriction of the Tangent Bundle of G/P to a Hypersurface
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 
$P$ be a maximal proper parabolic subgroup of a connected simple linear algebraic group 
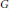$G$ , defined over 
$\mathbb{C}$ , such that 
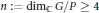$n\,:=\,{{\dim}_{\mathbb{C}}}\,G/P\,\ge \,4$ . Let 
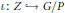$\iota :\,Z\,\to \,G/P$ be a reduced smooth hypersurface of degree at least 
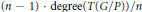$\left( n\,-\,1 \right)\,.\,\deg \text{ree}\left( T\left( G/P \right) \right)/n$ . We prove that the restriction of the tangent bundle 
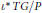${{\iota }^{*}}\,TG/P$ is semistable.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
References
[Br] Broer, A., A vanishing theorem for Dolbeault cohomology of homogeneous vector bundles. J. Reine Angew. Math.
493(1997), 153–169.Google Scholar
[Fl] Flenner, H., Restrictions of semistable bundles on projective varieties. Comment. Math. Helv.
59(1984), no. r4, 635–650. doi:10.1007/BF02566370Google Scholar
[Gr] Grothendieck, A., Cohomologie locale des faisceaux cohérents et théorĕmes de Lefschetz locaux et globaux. (SGA 2). Advanced Studies in Pure Mathematics, Vol. 2. North-Holland Publishing, Paris, 1968.Google Scholar
[Ko] Kobayashi, S., Differential Geometry of Complex Vector Bundles. Publications of the Mathematical Society of Japan 15. Princeton University Press, Princeton, NJ, 1987.Google Scholar
[Pa] Paoletti, R., Stability of Kapranov bundles on quadrics. Ann. Mat. Pura. Appl.
169(1995), 109–124. doi:10.1007/BF01759351Google Scholar
[RR] Ramanan, S. and Ramanathan, A., Some remarks on the instability flag. Tôhoku Math. J.
36(1984), no. 2, 269–291. doi:10.2748/tmj/1178228852Google Scholar
You have
Access