Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Laksov, Dan
2009.
A formalism for equivariant Schubert calculus.
Algebra & Number Theory,
Vol. 3,
Issue. 6,
p.
711.
Gatto, Letterio
and
Salehyan, Parham
2009.
Families of special Weierstrass points.
Comptes Rendus. Mathématique,
Vol. 347,
Issue. 21-22,
p.
1295.
Gatto, Letterio
and
Salehyan, Parham
2014.
The boson–fermion correspondence from linear ODEs.
Journal of Algebra,
Vol. 415,
Issue. ,
p.
162.
Gatto, Letterio
and
Salehyan, Parham
2016.
Hasse-Schmidt Derivations on Grassmann Algebras.
p.
81.
Gatto, Letterio
and
Salehyan, Parham
2016.
Hasse-Schmidt Derivations on Grassmann Algebras.
p.
63.
Anderson, Dave
and
Nigro, Antonio
2020.
Schubert Calculus and Its Applications in Combinatorics and Representation Theory.
Vol. 332,
Issue. ,
p.
113.
Gatto, Letterio
and
Salehyan, Parham
2020.
The cohomology of the Grassmannian is a gln-module.
Communications in Algebra,
Vol. 48,
Issue. 1,
p.
274.
Gatto, Letterio
and
Salehyan, Parham
2021.
Schubert Derivations on the Infinite Wedge Power.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 52,
Issue. 1,
p.
149.
Ricolfi, Andrea T.
2022.
An Invitation to Modern Enumerative Geometry.
Vol. 3,
Issue. ,
p.
57.
Behzad, Ommolbanin
and
Nejad, Abbas Nasrollah
2022.
Universal factorization algebras of polynomials represent Lie algebras of endomorphisms.
Journal of Algebra and Its Applications,
Vol. 21,
Issue. 04,
Bahadorykhalily, Fereshteh
2022.
Multivariate Hasse–Schmidt derivation on exterior algebras.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 14,
p.
2642.
Cotti, Giordano
Dubrovin, Boris A.
and
Guzzetti, Davide
2024.
Helix Structures in Quantum Cohomology of Fano Varieties.
Vol. 2356,
Issue. ,
p.
171.
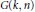 $G\left( k,\,n \right)$ is generated by certain derivations operating on an exterior algebra of a free module of rank
$G\left( k,\,n \right)$ is generated by certain derivations operating on an exterior algebra of a free module of rank  $n$ (Schubert calculus on a Grassmann algebra). Our main result gives, in a unified way, a presentation of all such cohomology rings in terms of generators and relations. Using results of Laksov and Thorup, it also provides a presentation of the universal factorization algebra of a monic polynomial of degree
$n$ (Schubert calculus on a Grassmann algebra). Our main result gives, in a unified way, a presentation of all such cohomology rings in terms of generators and relations. Using results of Laksov and Thorup, it also provides a presentation of the universal factorization algebra of a monic polynomial of degree  $n$ into the product of two monic polynomials, one of degree
$n$ into the product of two monic polynomials, one of degree  $k$ .
$k$ .