We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Please note, due to essential maintenance online purchasing will be unavailable between 08:00 and 12:00 (BST) on 24th February 2019. We apologise for any inconvenience.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the topology of the nontrivial component, 
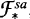, of self-adjoint Fredholm operators on a separable Hilbert space. In particular, if {Bt
} is a path of such operators, we can associate to {Bt
} an integer, sf({Bt
}), called the spectral flow of the path. This notion, due to M. Atiyah and G. Lusztig, assigns to the path {Bt
} the net number of eigenvalues (counted with multiplicities) which pass through 0 in the positive direction. There are difficulties in making this precise — the usual argument involves looking at the graph of the spectrum of the family (after a suitable perturbation) and then counting intersection numbers with y = 0.
We present a completely different approach using the functional calculus to obtain continuous paths of eigenprojections (at least locally) of the form 
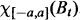. The spectral flow is then defined as the dimension of the nonnegative eigenspace at the end of this path minus the dimension of the nonnegative eigenspace at the beginning. This leads to an easy proof that spectral flow is a well-defined homomorphism from the homotopy groupoid of 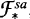onto Z. For the sake of completeness we also outline the seldom-mentioned proof that the restriction of spectral flow to 
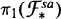is an isomorphism onto Z.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.
Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.
To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.
Email your librarian or administrator to recommend adding this journal to your organisation's collection.
