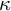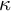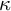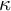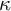1 Introduction
The method of forcing was developed by Paul Cohen in 1963 to prove that the Continuum Hypothesis cannot be proved from the Zermelo–Fraenkel set theory with the Axiom of Choice (
![]() $\mathsf {ZFC}$
). The technique works by picking a partial order approximating a “generic set” that can be added to a “ground model” of set theory while preserving the axioms of
$\mathsf {ZFC}$
). The technique works by picking a partial order approximating a “generic set” that can be added to a “ground model” of set theory while preserving the axioms of
![]() $\mathsf {ZFC}$
. We understand the general theory of forcing fairly well when working in
$\mathsf {ZFC}$
. We understand the general theory of forcing fairly well when working in
![]() $\mathsf {ZFC}$
. For example, if we chose a partial order which is countably distributive, then the generic extension of the universe will not have any new countable sequences of ground model elements. This property implies, among other things, that no new real numbers are added, and that
$\mathsf {ZFC}$
. For example, if we chose a partial order which is countably distributive, then the generic extension of the universe will not have any new countable sequences of ground model elements. This property implies, among other things, that no new real numbers are added, and that
![]() $\omega _1$
, the least uncountable cardinal, is the same between the ground model and its generic extension. On the other hand, we know that distributivity assumptions are not enough to prove that stationary subsets of
$\omega _1$
, the least uncountable cardinal, is the same between the ground model and its generic extension. On the other hand, we know that distributivity assumptions are not enough to prove that stationary subsets of
![]() $\omega _1$
remain stationary.Footnote
1
$\omega _1$
remain stationary.Footnote
1
Although the basic machinery of forcing does not rely on the Axiom of Choice, its general theory makes heavy use of it. This means that working over general models of Zermelo--Fraenkel ()
![]() $\mathsf {ZF}$
, where the Axiom of Choice is not necessarily assumed, is significantly harder: our intuition was honed in
$\mathsf {ZF}$
, where the Axiom of Choice is not necessarily assumed, is significantly harder: our intuition was honed in
![]() $\mathsf {ZFC}$
for many decades, and we still do not have a complete picture of what could go wrong, or how do our standard definitions behave in general models of
$\mathsf {ZFC}$
for many decades, and we still do not have a complete picture of what could go wrong, or how do our standard definitions behave in general models of
![]() $\mathsf {ZF}$
. With the recent advents of very large cardinal axioms,Footnote
2
e.g., Reinhardt and Berkeley cardinals whose existence refutes the Axiom of Choice, it is very important to better understand the theory of forcing in
$\mathsf {ZF}$
. With the recent advents of very large cardinal axioms,Footnote
2
e.g., Reinhardt and Berkeley cardinals whose existence refutes the Axiom of Choice, it is very important to better understand the theory of forcing in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
In this paper, we separate two properties which are equivalent in
![]() $\mathsf {ZFC}$
, namely, distributivity and adding new sequences of ground model objects, which we term “sequential.” Our main result is that this equivalence is not provable from
$\mathsf {ZFC}$
, namely, distributivity and adding new sequences of ground model objects, which we term “sequential.” Our main result is that this equivalence is not provable from
![]() $\mathsf {ZF}$
, or even
$\mathsf {ZF}$
, or even
![]() $\mathsf {ZF}$
augmented by the Principle of Dependent Choice (
$\mathsf {ZF}$
augmented by the Principle of Dependent Choice (
![]() $\mathsf {DC}$
) and its generalized versions. Moreover, we show that forcing with a distributive partial order must preserve the Axiom of Choice for countable families of sets (
$\mathsf {DC}$
) and its generalized versions. Moreover, we show that forcing with a distributive partial order must preserve the Axiom of Choice for countable families of sets (
![]() $\mathsf {AC}_{\omega }$
), but can violate
$\mathsf {AC}_{\omega }$
), but can violate
![]() $\mathsf {DC}$
, whereas a sequential partial order may even violate
$\mathsf {DC}$
, whereas a sequential partial order may even violate
![]() $\mathsf {AC}_{\omega }$
itself. We also provide a necessary and sufficient condition for a sequential partial order to preserve
$\mathsf {AC}_{\omega }$
itself. We also provide a necessary and sufficient condition for a sequential partial order to preserve
![]() $\mathsf {DC}$
, termed here “quasiproperness.”
$\mathsf {DC}$
, termed here “quasiproperness.”
Finally, we provide a partial answer to the question of whether or not the equivalence between the two properties is itself equivalent to the Axiom of Choice. We prove that in the Gitik model, where all the limit ordinals have countable cofinality, the equivalence between the two properties holds, whereas the Axiom of Choice fails quite badly. The one drawback is that the Gitik model requires assuming the consistency of suitable large cardinal axioms, which leaves the question of whether or not the equivalence can hold in the absence of the Axiom of Choice without these additional assumptions wide open.
In this paper, we begin by covering the basics of symmetric extensions, our main technical tool for constructions models of
![]() $\mathsf {ZF}$
. In Section 3, we study the basic properties of distributive and sequential forcings. Section 4 is dedicated for two minor results in the study of preservation of choice principles under generic extensions, we define a property akin to properness and show that it is equivalent to the preservation of
$\mathsf {ZF}$
. In Section 3, we study the basic properties of distributive and sequential forcings. Section 4 is dedicated for two minor results in the study of preservation of choice principles under generic extensions, we define a property akin to properness and show that it is equivalent to the preservation of
![]() $\mathsf {DC}$
, at least for sequential forcings. Section 5 is dedicated for our main theorem. Finally, Section 6 concludes the paper with several open questions that arise from this work.
$\mathsf {DC}$
, at least for sequential forcings. Section 5 is dedicated for our main theorem. Finally, Section 6 concludes the paper with several open questions that arise from this work.
2 Preliminaries
Throughout this paper, we work in
![]() $\mathsf {ZF}$
, unless specified otherwise. Our treatment of forcing will be standard. If
$\mathsf {ZF}$
, unless specified otherwise. Our treatment of forcing will be standard. If
![]() ${\mathbb P}$
is a notion of forcing, then
${\mathbb P}$
is a notion of forcing, then
![]() ${\mathbb P}$
is a preordered set with a maximum element denoted by
${\mathbb P}$
is a preordered set with a maximum element denoted by
![]() , or with the subscript omitted when clear from context. We write
, or with the subscript omitted when clear from context. We write
![]() $q\leq p$
to mean that q is a stronger condition than p, or that it extends p. Two conditions are compatible if they have a common extension. We will also follow Goldstern’s alphabet convention, so p is never a stronger condition than q, etc.
$q\leq p$
to mean that q is a stronger condition than p, or that it extends p. Two conditions are compatible if they have a common extension. We will also follow Goldstern’s alphabet convention, so p is never a stronger condition than q, etc.
When given a collection of
![]() ${\mathbb P}$
-names,
${\mathbb P}$
-names,
![]() $\{\dot x_i\mid i\in I\}$
, we will denote by
$\{\dot x_i\mid i\in I\}$
, we will denote by
![]() $\{\dot x_i\mid i\in I\}^{\bullet }$
the canonical name this class generates:
$\{\dot x_i\mid i\in I\}^{\bullet }$
the canonical name this class generates:
![]() . This notation extends naturally to ordered pairs and functions whose domain is in the ground model. We will also say that
. This notation extends naturally to ordered pairs and functions whose domain is in the ground model. We will also say that
![]() $\dot y$
appears in
$\dot y$
appears in
![]() $\dot x$
if there is some
$\dot x$
if there is some
![]() $p\in {\mathbb P}$
such that
$p\in {\mathbb P}$
such that
![]() $\langle p,\dot y\rangle \in \dot x$
.
$\langle p,\dot y\rangle \in \dot x$
.
Given a set X, we use
![]() $|X|$
to denote its cardinal number. If X can be well-ordered, then
$|X|$
to denote its cardinal number. If X can be well-ordered, then
![]() $|X|$
is simply the least ordinal equipotent with X. Otherwise, we use the Scott cardinal of X which is the set
$|X|$
is simply the least ordinal equipotent with X. Otherwise, we use the Scott cardinal of X which is the set
![]() $\{Y\in V_{\alpha }\mid \exists f\colon X\to Y\text { a bijection}\}$
with
$\{Y\in V_{\alpha }\mid \exists f\colon X\to Y\text { a bijection}\}$
with
![]() $\alpha $
taken as the least ordinal for which the set is nonempty. Greek letters, when used as cardinals, will always refer to well-ordered cardinals. We will denote by
$\alpha $
taken as the least ordinal for which the set is nonempty. Greek letters, when used as cardinals, will always refer to well-ordered cardinals. We will denote by
![]() $\mathrm {COrd}$
the class of well-orderable cardinals, that is the finite ordinals and the
$\mathrm {COrd}$
the class of well-orderable cardinals, that is the finite ordinals and the
![]() $\aleph $
numbers.
$\aleph $
numbers.
We write
![]() $|X|\leq |Y|$
to mean that there is an injection from X into Y, and we write
$|X|\leq |Y|$
to mean that there is an injection from X into Y, and we write
![]() $|X|<|Y|$
to mean that there is an injection, but there is no injection from Y into X. Note that unlike in the case of
$|X|<|Y|$
to mean that there is an injection, but there is no injection from Y into X. Note that unlike in the case of
![]() $\mathsf {ZFC}$
, writing
$\mathsf {ZFC}$
, writing
![]() $|X|\nleq |Y|$
does not imply that
$|X|\nleq |Y|$
does not imply that
![]() $|Y|<|X|$
.
$|Y|<|X|$
.
We write
![]() $|X|\leq ^*|Y|$
to mean that there is a surjection from a subset of Y onto X.Footnote
3
This relation is transitive, not necessarily antisymmetric (unlike
$|X|\leq ^*|Y|$
to mean that there is a surjection from a subset of Y onto X.Footnote
3
This relation is transitive, not necessarily antisymmetric (unlike
![]() $\leq $
).
$\leq $
).
The axiom
![]() $\mathsf {AC}_X$
states that given any family of nonempty set indexed by X admits a choice function, we omit X to mean
$\mathsf {AC}_X$
states that given any family of nonempty set indexed by X admits a choice function, we omit X to mean
![]() $\forall X\,\mathsf {AC}_X$
. For an infinite cardinal
$\forall X\,\mathsf {AC}_X$
. For an infinite cardinal
![]() $\kappa $
, the axiom
$\kappa $
, the axiom
![]() $\mathsf {DC}_{\kappa }$
states that every
$\mathsf {DC}_{\kappa }$
states that every
![]() $\kappa $
-closed treeFootnote
4
has a maximal element or a chain of order type
$\kappa $
-closed treeFootnote
4
has a maximal element or a chain of order type
![]() $\kappa $
. We write
$\kappa $
. We write
![]() $\mathsf {DC}_{<\kappa }$
to mean
$\mathsf {DC}_{<\kappa }$
to mean
![]() $(\forall \lambda <\kappa )\mathsf {DC}_{\lambda }$
. In the case of
$(\forall \lambda <\kappa )\mathsf {DC}_{\lambda }$
. In the case of
![]() $\mathsf {DC}_{\omega }$
, we simply write
$\mathsf {DC}_{\omega }$
, we simply write
![]() $\mathsf {DC}$
.
$\mathsf {DC}$
.
2.1 Symmetric extensions
Forcing is an extremely versatile technique when it comes to independence proofs. It has one drawback: a generic extension of a model of
![]() $\mathsf {ZFC}$
is a model of
$\mathsf {ZFC}$
is a model of
![]() $\mathsf {ZFC}$
.Footnote
5
But we can extend the technique of forcing. By imitating the Fraenkel–Mostowski–Specker technique for permutation models,Footnote
6
we can identify a class of names which defines an intermediate model, between the ground model and its generic extension, where the Axiom of Choice may fail.
$\mathsf {ZFC}$
.Footnote
5
But we can extend the technique of forcing. By imitating the Fraenkel–Mostowski–Specker technique for permutation models,Footnote
6
we can identify a class of names which defines an intermediate model, between the ground model and its generic extension, where the Axiom of Choice may fail.
Let
![]() ${\mathbb P}$
be a fixed forcing notion. If
${\mathbb P}$
be a fixed forcing notion. If
![]() $\pi $
is an automorphism of
$\pi $
is an automorphism of
![]() ${\mathbb P}$
, then
${\mathbb P}$
, then
![]() $\pi $
extends to
$\pi $
extends to
![]() ${\mathbb P}$
-names by recursion:
${\mathbb P}$
-names by recursion:
Seeing how the forcing relation is defined from the order, the following lemma is not surprising. For a proof of this lemma, see Lemma 14.37 in [Reference Jech5].
Lemma (The Symmetry Lemma)
Let
![]() ${\mathbb P}$
be a forcing,
${\mathbb P}$
be a forcing,
![]() $\pi $
an automorphism of
$\pi $
an automorphism of
![]() ${\mathbb P}$
,
${\mathbb P}$
,
![]() $p\in {\mathbb P}$
, and
$p\in {\mathbb P}$
, and
![]() $\dot x$
some
$\dot x$
some
![]() ${\mathbb P}$
-name. Then,
${\mathbb P}$
-name. Then,
Let
![]() $\mathscr {G}$
be a group, we say that
$\mathscr {G}$
be a group, we say that
![]() $\mathscr {F}$
is a filter of subgroups if it is a nonempty collection of subgroups of
$\mathscr {F}$
is a filter of subgroups if it is a nonempty collection of subgroups of
![]() $\mathscr {G}$
which is closed under supergroups and finite intersections. We say that
$\mathscr {G}$
which is closed under supergroups and finite intersections. We say that
![]() $\mathscr {F}$
is normal if whenever
$\mathscr {F}$
is normal if whenever
![]() $H\in \mathscr {G}$
and
$H\in \mathscr {G}$
and
![]() $\pi \in \mathscr {G}$
, then
$\pi \in \mathscr {G}$
, then
![]() $\pi H\pi ^{-1}\in \mathscr {F}$
as well.
$\pi H\pi ^{-1}\in \mathscr {F}$
as well.
We say that
![]() $\langle {\mathbb P},\mathscr {G},\mathscr {F}\rangle $
is a symmetric system if
$\langle {\mathbb P},\mathscr {G},\mathscr {F}\rangle $
is a symmetric system if
![]() ${\mathbb P}$
is a forcing notion,
${\mathbb P}$
is a forcing notion,
![]() $\mathscr {G}$
is a group of automorphisms of
$\mathscr {G}$
is a group of automorphisms of
![]() ${\mathbb P}$
, and
${\mathbb P}$
, and
![]() $\mathscr {F}$
is a normal filter of subgroups of on
$\mathscr {F}$
is a normal filter of subgroups of on
![]() $\mathscr {G}$
. Given such symmetric system, a
$\mathscr {G}$
. Given such symmetric system, a
![]() ${\mathbb P}$
-name,
${\mathbb P}$
-name,
![]() $\dot x$
, is
$\dot x$
, is
![]() $\mathscr {F}$
-symmetric if
$\mathscr {F}$
-symmetric if
![]() $\operatorname {\mathrm {sym}}_{\mathscr {G}}(\dot x)=\{\pi \in \mathscr {G}\mid \pi \dot x=\dot x\}\in \mathscr {F}$
. We say that
$\operatorname {\mathrm {sym}}_{\mathscr {G}}(\dot x)=\{\pi \in \mathscr {G}\mid \pi \dot x=\dot x\}\in \mathscr {F}$
. We say that
![]() $\dot x$
is hereditarily
$\dot x$
is hereditarily
![]() $\mathscr {F}$
-symmetric, if this notion holds for every
$\mathscr {F}$
-symmetric, if this notion holds for every
![]() ${\mathbb P}$
-name hereditarily appearing in
${\mathbb P}$
-name hereditarily appearing in
![]() $\dot x$
. We denote by
$\dot x$
. We denote by
![]() $\mathsf {HS}_{\mathscr {F}}$
the class of hereditarily
$\mathsf {HS}_{\mathscr {F}}$
the class of hereditarily
![]() $\mathscr {F}$
-symmetric names.
$\mathscr {F}$
-symmetric names.
Theorem Let
![]() $\langle {\mathbb P},\mathscr {G},\mathscr {F}\rangle $
be a symmetric system, let
$\langle {\mathbb P},\mathscr {G},\mathscr {F}\rangle $
be a symmetric system, let
![]() $G\subseteq {\mathbb P}$
be a V-generic filter, and let M denote the class
$G\subseteq {\mathbb P}$
be a V-generic filter, and let M denote the class
![]() $\mathsf {HS}_{\mathscr {F}}^G=\{\dot x^G\mid \dot x\in \mathsf {HS}_{\mathscr {F}}\}$
. Then M is a transitive model of
$\mathsf {HS}_{\mathscr {F}}^G=\{\dot x^G\mid \dot x\in \mathsf {HS}_{\mathscr {F}}\}$
. Then M is a transitive model of
![]() $\mathsf {ZF}$
satisfying
$\mathsf {ZF}$
satisfying
![]() $V\subseteq M\subseteq V[G]$
.
$V\subseteq M\subseteq V[G]$
.
We say that M as in the theorem above, whose proof appears as Lemma 15.51 in [Reference Jech5], is a symmetric extension of V. The symmetric extensions of V were studied recently by Usuba in [Reference Usuba, Arai, Kikuchi, Kuroda, Okada and Yorioka12, Reference Usuba13]. It is tempting to think that every intermediate model of
![]() $\mathsf {ZF}$
is a symmetric extension, but this is not true, as was shown in [Reference Karagila7].
$\mathsf {ZF}$
is a symmetric extension, but this is not true, as was shown in [Reference Karagila7].
Since we will only have a single symmetric extension of concern at each step, even if we will force over it, we will omit the subscripts from the notation from here on out.
Finally, we have a forcing relation for symmetric extensions,
![]() $\mathrel {\Vdash }^{\mathsf {HS}}$
defined by relativising the
$\mathrel {\Vdash }^{\mathsf {HS}}$
defined by relativising the
![]() $\mathrel {\Vdash }$
relation to the class
$\mathrel {\Vdash }$
relation to the class
![]() $\mathsf {HS}$
. This relation has the same properties and behavior as the standard
$\mathsf {HS}$
. This relation has the same properties and behavior as the standard
![]() $\mathrel {\Vdash }$
relation. Moreover, if
$\mathrel {\Vdash }$
relation. Moreover, if
![]() $\pi \in \mathscr {G}$
, then the Symmetry Lemma holds also for
$\pi \in \mathscr {G}$
, then the Symmetry Lemma holds also for
![]() $\mathrel {\Vdash }^{\mathsf {HS}}$
.
$\mathrel {\Vdash }^{\mathsf {HS}}$
.
We conclude this introduction with a general example.
Example 2.1 Let
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda $
be regular cardinals such that
$\lambda $
be regular cardinals such that
![]() $\lambda \geq \kappa $
and suppose that
$\lambda \geq \kappa $
and suppose that
![]() ${\kappa ^{<\kappa }=\kappa }$
. Let
${\kappa ^{<\kappa }=\kappa }$
. Let
![]() ${\mathbb P}$
be the forcing
${\mathbb P}$
be the forcing
![]() $\operatorname {\mathrm {Add}}(\kappa ,\lambda )$
, whose conditions are partial functions
$\operatorname {\mathrm {Add}}(\kappa ,\lambda )$
, whose conditions are partial functions
![]() $p\colon \lambda \times \kappa \to 2$
such that
$p\colon \lambda \times \kappa \to 2$
such that
![]() $|p|<\kappa $
, the projection of p onto its
$|p|<\kappa $
, the projection of p onto its
![]() $\lambda $
component is called the support of p and is denoted by
$\lambda $
component is called the support of p and is denoted by
![]() $\operatorname {\mathrm {supp}} p$
. We let
$\operatorname {\mathrm {supp}} p$
. We let
![]() $\mathscr {G}$
be the group of permutations of
$\mathscr {G}$
be the group of permutations of
![]() $\lambda $
, and
$\lambda $
, and
![]() $\pi \in \mathscr {G}$
acts on
$\pi \in \mathscr {G}$
acts on
![]() ${\mathbb P}$
by letting
${\mathbb P}$
by letting
Finally, let the filter of subgroups be generated by
![]() $\{\operatorname {\mathrm {fix}}(E)\mid E\in [\lambda ]^{<\lambda }\}$
, where
$\{\operatorname {\mathrm {fix}}(E)\mid E\in [\lambda ]^{<\lambda }\}$
, where
![]() $\operatorname {\mathrm {fix}}(E)=\{\pi \in \mathscr {G}\mid \pi \mathbin \upharpoonright E=\operatorname {\mathrm {id}}\}$
.
$\operatorname {\mathrm {fix}}(E)=\{\pi \in \mathscr {G}\mid \pi \mathbin \upharpoonright E=\operatorname {\mathrm {id}}\}$
.
We denote by
![]() $\dot a_{\alpha }$
, for
$\dot a_{\alpha }$
, for
![]() $\alpha <\lambda $
, the name of the
$\alpha <\lambda $
, the name of the
![]() $\alpha $
th generic subset:
$\alpha $
th generic subset:
We will denote by
![]() $\dot A$
the name
$\dot A$
the name
![]() $\{\dot a_{\alpha }\mid \alpha <\lambda \}^{\bullet }$
. Let G be a V-generic filter and let M be the corresponding symmetric extension, we will omit the dots to indicate the interpretation of the names in M. We will show that the following hold in M:
$\{\dot a_{\alpha }\mid \alpha <\lambda \}^{\bullet }$
. Let G be a V-generic filter and let M be the corresponding symmetric extension, we will omit the dots to indicate the interpretation of the names in M. We will show that the following hold in M:
-
(1) Every well-orderable subset of A has size
 $<\lambda $
.
$<\lambda $
. -
(2)
 $\mathsf {DC}_{<\lambda }+\lnot \mathsf {AC}$
.
$\mathsf {DC}_{<\lambda }+\lnot \mathsf {AC}$
.
First, we observe that
![]() $\pi \dot a_{\alpha }=\dot a_{\pi \alpha }$
, and since all the names appearing in
$\pi \dot a_{\alpha }=\dot a_{\pi \alpha }$
, and since all the names appearing in
![]() $\dot a_{\alpha }$
are canonical ground model names,
$\dot a_{\alpha }$
are canonical ground model names,
![]() $\operatorname {\mathrm {fix}}(\{\alpha \})$
witnesses that
$\operatorname {\mathrm {fix}}(\{\alpha \})$
witnesses that
![]() $\dot a_{\alpha }\in \mathsf {HS}$
. Consequently,
$\dot a_{\alpha }\in \mathsf {HS}$
. Consequently,
![]() ${\pi \dot A=\dot A}$
for all
${\pi \dot A=\dot A}$
for all
![]() $\pi \in \mathscr {G}$
. Therefore, each
$\pi \in \mathscr {G}$
. Therefore, each
![]() $a_{\alpha }$
and A itself are all in M.
$a_{\alpha }$
and A itself are all in M.
Suppose that
![]() $\dot B\in \mathsf {HS}$
and
$\dot B\in \mathsf {HS}$
and
![]() $p\mathrel {\Vdash }^{\mathsf {HS}}"\dot B\subseteq \dot A$
and can be well-ordered.” Let
$p\mathrel {\Vdash }^{\mathsf {HS}}"\dot B\subseteq \dot A$
and can be well-ordered.” Let
![]() $E\subseteq \lambda $
be such that
$E\subseteq \lambda $
be such that
![]() $\operatorname {\mathrm {fix}}(E)\subseteq \operatorname {\mathrm {sym}}(\dot f)$
, where
$\operatorname {\mathrm {fix}}(E)\subseteq \operatorname {\mathrm {sym}}(\dot f)$
, where
![]() $p\mathrel {\Vdash }^{\mathsf {HS}}\text {"}\dot f\colon \dot B\to \check \eta $
is an injective function,” and we may also assume that
$p\mathrel {\Vdash }^{\mathsf {HS}}\text {"}\dot f\colon \dot B\to \check \eta $
is an injective function,” and we may also assume that
![]() $\operatorname {\mathrm {supp}} p\subseteq E$
. Note that
$\operatorname {\mathrm {supp}} p\subseteq E$
. Note that
![]() $\operatorname {\mathrm {fix}}(E)\subseteq \operatorname {\mathrm {sym}}(\dot B)$
as well.
$\operatorname {\mathrm {fix}}(E)\subseteq \operatorname {\mathrm {sym}}(\dot B)$
as well.
Let
![]() $\alpha <\lambda $
be such that
$\alpha <\lambda $
be such that
![]() $\alpha \notin E$
, and let
$\alpha \notin E$
, and let
![]() $q\leq p$
be a condition such that
$q\leq p$
be a condition such that
![]() $q\mathrel {\Vdash }^{\mathsf {HS}}\dot a_{\alpha }\in \dot B$
and without loss of generality, we also assume that for some
$q\mathrel {\Vdash }^{\mathsf {HS}}\dot a_{\alpha }\in \dot B$
and without loss of generality, we also assume that for some
![]() $\delta <\eta $
,
$\delta <\eta $
,
![]() $q\mathrel {\Vdash }^{\mathsf {HS}}\dot f(\dot a_{\alpha })=\check \delta $
.
$q\mathrel {\Vdash }^{\mathsf {HS}}\dot f(\dot a_{\alpha })=\check \delta $
.
Since
![]() $\operatorname {\mathrm {supp}} q$
is of size
$\operatorname {\mathrm {supp}} q$
is of size
![]() $<\kappa $
, we can find
$<\kappa $
, we can find
![]() $\beta \notin \operatorname {\mathrm {supp}} q\cup E$
and consider
$\beta \notin \operatorname {\mathrm {supp}} q\cup E$
and consider
![]() $\pi $
to be the automorphism defined by the
$\pi $
to be the automorphism defined by the
![]() $2$
-cycle
$2$
-cycle
![]() $(\alpha \ \beta )$
. By the choice of
$(\alpha \ \beta )$
. By the choice of
![]() $\alpha ,$
we immediately have that
$\alpha ,$
we immediately have that
![]() $\pi \in \operatorname {\mathrm {fix}}(E)$
and therefore
$\pi \in \operatorname {\mathrm {fix}}(E)$
and therefore
![]() $\pi p=p,\pi \dot B=\dot B,\pi \dot f=\dot f$
. Applying these, along with the Symmetry Lemma, we get that
$\pi p=p,\pi \dot B=\dot B,\pi \dot f=\dot f$
. Applying these, along with the Symmetry Lemma, we get that
![]() $\pi q\mathrel {\Vdash }^{\mathsf {HS}}\dot f(\dot a_{\alpha })=\check \delta $
. But
$\pi q\mathrel {\Vdash }^{\mathsf {HS}}\dot f(\dot a_{\alpha })=\check \delta $
. But
![]() $\pi q$
is compatible with q, as we only moved one coordinate to a previously empty one. This means that
$\pi q$
is compatible with q, as we only moved one coordinate to a previously empty one. This means that
![]() $r=q\cup \pi q$
is a condition which forces both “
$r=q\cup \pi q$
is a condition which forces both “
![]() $\dot f$
is injective” and
$\dot f$
is injective” and
![]() $\dot f(\dot a_{\alpha })=\dot f(\dot a_{\beta })$
. This is of course impossible. This means that there is no such q, and therefore if
$\dot f(\dot a_{\alpha })=\dot f(\dot a_{\beta })$
. This is of course impossible. This means that there is no such q, and therefore if
![]() $\alpha \notin E$
,
$\alpha \notin E$
,
![]() $p\mathrel {\Vdash }^{\mathsf {HS}}\dot a_{\alpha }\notin \dot B$
. Since
$p\mathrel {\Vdash }^{\mathsf {HS}}\dot a_{\alpha }\notin \dot B$
. Since
![]() $E\in [\lambda ]^{<\lambda }$
, and since
$E\in [\lambda ]^{<\lambda }$
, and since
![]() $\lambda $
was not collapsed in
$\lambda $
was not collapsed in
![]() $V[G]$
, the conclusion holds.
$V[G]$
, the conclusion holds.
This immediately shows that
![]() $\lnot \mathsf {AC}$
holds as well. To get
$\lnot \mathsf {AC}$
holds as well. To get
![]() $\mathsf {DC}_{<\lambda }$
, we appeal to [Reference Karagila8], where the folklore results about preservation of DC principles are formalized. Specifically, if
$\mathsf {DC}_{<\lambda }$
, we appeal to [Reference Karagila8], where the folklore results about preservation of DC principles are formalized. Specifically, if
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\lambda $
-closed or has
$\lambda $
-closed or has
![]() $\lambda $
-c.c., which in this case follows from the assumption
$\lambda $
-c.c., which in this case follows from the assumption
![]() $\kappa ^{<\kappa }=\kappa $
, and
$\kappa ^{<\kappa }=\kappa $
, and
![]() $\mathscr {F}$
is
$\mathscr {F}$
is
![]() $\lambda $
-complete, then
$\lambda $
-complete, then
![]() $\mathsf {DC}_{<\lambda }$
holds in the symmetric extension.
$\mathsf {DC}_{<\lambda }$
holds in the symmetric extension.
In the case
![]() $\lambda =\kappa ,$
we refer to this model as the
$\lambda =\kappa ,$
we refer to this model as the
![]() $\kappa $
-Cohen model, and if
$\kappa $
-Cohen model, and if
![]() $\kappa =\omega $
we omit it altogether. The Cohen model is one of the most important models of
$\kappa =\omega $
we omit it altogether. The Cohen model is one of the most important models of
![]() $\mathsf {ZF}+\lnot \mathsf {AC}$
. It satisfies the Boolean Prime Ideal theorem, and has many interesting properties. For a complete exposition, see Chapter 5 in [Reference Jech6].
$\mathsf {ZF}+\lnot \mathsf {AC}$
. It satisfies the Boolean Prime Ideal theorem, and has many interesting properties. For a complete exposition, see Chapter 5 in [Reference Jech6].
3 Distributive and sequential forcings
Definition 3.1 A forcing notion
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\leq }|X|$
-distributive if whenever
${\leq }|X|$
-distributive if whenever
![]() $\langle D_x\mid x\in X\rangle $
is a family of dense open sets,
$\langle D_x\mid x\in X\rangle $
is a family of dense open sets,
![]() $\bigcap _{x\in X}D_x$
is a dense open set.Footnote
7
If X can be well-ordered, we will use the standard notation of
$\bigcap _{x\in X}D_x$
is a dense open set.Footnote
7
If X can be well-ordered, we will use the standard notation of
![]() $\kappa $
-distributive to mean “for all
$\kappa $
-distributive to mean “for all
![]() $\lambda <\kappa $
,
$\lambda <\kappa $
,
![]() ${\leq }\lambda $
-distributive,” and we will use
${\leq }\lambda $
-distributive,” and we will use
![]() $\sigma $
-distributive to mean
$\sigma $
-distributive to mean
![]() $\aleph _1$
-distributive.
$\aleph _1$
-distributive.
To make the definition smoother, we consider the intersection as bounded by
![]() ${\mathbb P}$
, namely
${\mathbb P}$
, namely
![]() $\bigcap _{x\in X}D_x=\{p\in {\mathbb P}\mid \forall x\in X, p\in D_x\}$
. This has the benefit that for
$\bigcap _{x\in X}D_x=\{p\in {\mathbb P}\mid \forall x\in X, p\in D_x\}$
. This has the benefit that for
![]() $X=\varnothing $
,
$X=\varnothing $
,
![]() $\bigcap _{x\in X}D_x={\mathbb P}$
.
$\bigcap _{x\in X}D_x={\mathbb P}$
.
Proposition 3.2 If
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\leq }|X|$
-distributive and
${\leq }|X|$
-distributive and
![]() $|Y|\leq ^*|X|$
, then
$|Y|\leq ^*|X|$
, then
![]() ${\mathbb P}$
is also
${\mathbb P}$
is also
![]() ${\leq }|Y|$
-distributive.
${\leq }|Y|$
-distributive.
Proof Let
![]() $f\colon X\to Y$
be a surjective function (for
$f\colon X\to Y$
be a surjective function (for
![]() $Y=\varnothing $
the conclusion is vacuously true), if
$Y=\varnothing $
the conclusion is vacuously true), if
![]() $\langle D_y\mid y\in Y\rangle $
is a family of dense open sets, let
$\langle D_y\mid y\in Y\rangle $
is a family of dense open sets, let
![]() $E_x=D_{f(x)}$
, then
$E_x=D_{f(x)}$
, then
![]() $\langle E_x\mid x\in X\rangle $
is a family of dense open sets indexed by X and therefore its intersection is dense. Easily,
$\langle E_x\mid x\in X\rangle $
is a family of dense open sets indexed by X and therefore its intersection is dense. Easily,
![]() $\bigcap _{y\in Y}D_y=\bigcap _{x\in X}E_x$
, and so
$\bigcap _{y\in Y}D_y=\bigcap _{x\in X}E_x$
, and so
![]() $\bigcap _{y\in Y}D_y$
is dense.
$\bigcap _{y\in Y}D_y$
is dense.
Definition 3.3 Let
![]() ${ \mathcal{D}}$
be a class (possibly proper) of cardinals. We define the following properties:
${ \mathcal{D}}$
be a class (possibly proper) of cardinals. We define the following properties:
-
(1)
 $ \mathcal D$
is
$ \mathcal D$
is
 $*$
-closed if whenever
$*$
-closed if whenever
 $|X|\in \mathcal D$
and
$|X|\in \mathcal D$
and
 $|Y|\leq ^*|X|$
, then
$|Y|\leq ^*|X|$
, then
 $|Y|\in \mathcal D$
.Footnote
8
$|Y|\in \mathcal D$
.Footnote
8
-
(2)
 $ \mathcal D$
is union-regular if it is directed and whenever
$ \mathcal D$
is union-regular if it is directed and whenever
 $|X|\in \mathcal D$
and
$|X|\in \mathcal D$
and
 $\langle A_x\mid x\in X\rangle $
is a sequence of sets such that
$\langle A_x\mid x\in X\rangle $
is a sequence of sets such that
 $|A_x|\in \mathcal D$
for all
$|A_x|\in \mathcal D$
for all
 $x\in X$
, then there is some
$x\in X$
, then there is some
 $|A|\in \mathcal D$
such that for all x,
$|A|\in \mathcal D$
such that for all x,
 $|A_x|\leq |A|$
.
$|A_x|\leq |A|$
.
Theorem 3.4 Let
![]() ${\mathbb P}$
be a forcing, and let
${\mathbb P}$
be a forcing, and let
![]() $ \mathcal D$
be the class of cardinals such that
$ \mathcal D$
be the class of cardinals such that
![]() $|X|\in \mathcal D$
if and only if
$|X|\in \mathcal D$
if and only if
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\leq }|X|$
-distributive. Then,
${\leq }|X|$
-distributive. Then,
![]() $\omega \subseteq \mathcal D$
and
$\omega \subseteq \mathcal D$
and
![]() $ \mathcal D$
is
$ \mathcal D$
is
![]() $*$
-closed and union-regular.
$*$
-closed and union-regular.
Proof The fact that
![]() $\omega \subseteq \mathcal D$
is trivial. The fact that it is
$\omega \subseteq \mathcal D$
is trivial. The fact that it is
![]() $*$
-closed follows from Proposition 3.2. Finally, suppose that
$*$
-closed follows from Proposition 3.2. Finally, suppose that
![]() $|X|\in \mathcal D$
and for each
$|X|\in \mathcal D$
and for each
![]() $x\in X$
,
$x\in X$
,
![]() $A_x$
is some set such that
$A_x$
is some set such that
![]() $|A_x|\in \mathcal D$
, without loss of generality assume that
$|A_x|\in \mathcal D$
, without loss of generality assume that
![]() $A_x$
are disjoint, since the disjoint union maps onto the union in the obvious way and
$A_x$
are disjoint, since the disjoint union maps onto the union in the obvious way and
![]() $ \mathcal D$
is
$ \mathcal D$
is
![]() $*$
-closed.
$*$
-closed.
Let
![]() $A=\bigcup _{x\in X} A_x$
and suppose that
$A=\bigcup _{x\in X} A_x$
and suppose that
![]() $\langle D_a\mid a\in A\rangle $
is a family of dense open subsets of
$\langle D_a\mid a\in A\rangle $
is a family of dense open subsets of
![]() ${\mathbb P}$
. For each
${\mathbb P}$
. For each
![]() $x\in X$
, consider
$x\in X$
, consider
![]() $\langle D_a\mid a\in A_x\rangle $
, then due to the fact that
$\langle D_a\mid a\in A_x\rangle $
, then due to the fact that
![]() $|A_x|\in \mathcal D$
, we can replace
$|A_x|\in \mathcal D$
, we can replace
![]() $\langle D_a\mid a\in A_x\rangle $
by its intersection,
$\langle D_a\mid a\in A_x\rangle $
by its intersection,
![]() $E_x$
. This means that
$E_x$
. This means that
![]() $\bigcap _{a\in A}D_a$
is the same as
$\bigcap _{a\in A}D_a$
is the same as
![]() $\bigcap _{x\in X}E_x$
, but since
$\bigcap _{x\in X}E_x$
, but since
![]() $|X|\in \mathcal D$
as well, the intersection is dense as wanted.
$|X|\in \mathcal D$
as well, the intersection is dense as wanted.
We will refer to
![]() $ \mathcal D$
in the theorem as the distributivity spectrum of
$ \mathcal D$
in the theorem as the distributivity spectrum of
![]() ${\mathbb P}$
and denote it by
${\mathbb P}$
and denote it by
![]() $ \mathcal D_{\mathbb P}$
.
$ \mathcal D_{\mathbb P}$
.
Corollary 3.5 Suppose that
![]() $\operatorname {\mathrm {cf}}(\alpha )=\omega $
for any limit ordinal
$\operatorname {\mathrm {cf}}(\alpha )=\omega $
for any limit ordinal
![]() $\alpha $
. If
$\alpha $
. If
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\sigma $
-distributive, then
$\sigma $
-distributive, then
![]() $\mathrm {COrd}\subseteq \mathcal D_{\mathbb P}$
. Moreover, suppose that every set in V is generated by iterating countable unions starting with the class
$\mathrm {COrd}\subseteq \mathcal D_{\mathbb P}$
. Moreover, suppose that every set in V is generated by iterating countable unions starting with the class
![]() $[V]^{\leq \omega }$
, then any
$[V]^{\leq \omega }$
, then any
![]() $\sigma $
-distributive forcing is trivial.Footnote
9
$\sigma $
-distributive forcing is trivial.Footnote
9
The conditions above seem fantastic, especially the latter, but they are indeed consistent with
![]() $\mathsf {ZF}$
,Footnote
10
as shown by Gitik in [Reference Gitik4, Theorem 6.3].
$\mathsf {ZF}$
,Footnote
10
as shown by Gitik in [Reference Gitik4, Theorem 6.3].
Definition 3.6 We say that a forcing
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\leq }|X|$
-sequential if whenever
${\leq }|X|$
-sequential if whenever
![]() $G\subseteq {\mathbb P}$
is V-generic and
$G\subseteq {\mathbb P}$
is V-generic and
![]() $f\in V[G]$
is a function
$f\in V[G]$
is a function
![]() $f\colon X\to V$
, then
$f\colon X\to V$
, then
![]() $f\in V$
. The same caveats regarding well-ordered X will apply here as they do for distributivity.
$f\in V$
. The same caveats regarding well-ordered X will apply here as they do for distributivity.
Proposition 3.7 Suppose that
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\leq }|X|$
-distributive, then it is
${\leq }|X|$
-distributive, then it is
![]() ${\leq }|X|$
-sequential.
${\leq }|X|$
-sequential.
Proof Suppose that
![]() $\dot f$
is a
$\dot f$
is a
![]() ${\mathbb P}$
-name such that
${\mathbb P}$
-name such that
![]() , for some
, for some
![]() $\alpha $
, defining
$\alpha $
, defining
![]() $D_x=\{p\in {\mathbb P}\mid \exists y(p\mathrel {\Vdash }\dot f(\check x)=\check y\}$
, we have that
$D_x=\{p\in {\mathbb P}\mid \exists y(p\mathrel {\Vdash }\dot f(\check x)=\check y\}$
, we have that
![]() $D_x$
is a dense open set. By distributivity,
$D_x$
is a dense open set. By distributivity,
![]() $D=\bigcap _{x\in X}D_x$
is dense, and if
$D=\bigcap _{x\in X}D_x$
is dense, and if
![]() $p\in D$
, we define
$p\in D$
, we define
![]() $f_p(x)=y$
if and only if
$f_p(x)=y$
if and only if
![]() ${p\mathrel {\Vdash }\dot f(\check x)=\check y}$
. Since
${p\mathrel {\Vdash }\dot f(\check x)=\check y}$
. Since
![]() $p\in D_x$
for all
$p\in D_x$
for all
![]() $x\in X$
, this function is well-defined, and easily
$x\in X$
, this function is well-defined, and easily
![]() $p\mathrel {\Vdash }\dot f=\check f_p$
.
$p\mathrel {\Vdash }\dot f=\check f_p$
.
It is a standard exercise that assuming
![]() $\mathsf {ZFC}$
,
$\mathsf {ZFC}$
,
![]() ${\leq }|X|$
-sequential also implies
${\leq }|X|$
-sequential also implies
![]() ${\leq }|X|$
-distributive. The proof, however, relies on the fact that every dense open set contains a maximal antichain (which makes the generic filter act as a choice function). As we will see in Section 5, this reliance on the Axiom of Choice is crucial.
${\leq }|X|$
-distributive. The proof, however, relies on the fact that every dense open set contains a maximal antichain (which makes the generic filter act as a choice function). As we will see in Section 5, this reliance on the Axiom of Choice is crucial.
Nevertheless, defining the sequentiality spectrum of a forcing
![]() ${\mathbb P}$
, denoted by
${\mathbb P}$
, denoted by
![]() $ \mathcal S_{\mathbb P}$
, in an analogous manner to the distributivity spectrum, the proofs of Theorem 3.4 and Corollary 3.5 work also for the sequentiality spectrum.
$ \mathcal S_{\mathbb P}$
, in an analogous manner to the distributivity spectrum, the proofs of Theorem 3.4 and Corollary 3.5 work also for the sequentiality spectrum.
Corollary 3.8 It is consistent with
![]() $\mathsf {ZF}+\lnot \mathsf {AC}$
that for every X, every
$\mathsf {ZF}+\lnot \mathsf {AC}$
that for every X, every
![]() ${\leq }|X|$
-sequential forcing is
${\leq }|X|$
-sequential forcing is
![]() ${\leq }|X|$
-distributive.
${\leq }|X|$
-distributive.
Proof First, we will show that in Gitik’s model every
![]() $\sigma $
-sequential forcing is trivial. Define a rank function in the following way:
$\sigma $
-sequential forcing is trivial. Define a rank function in the following way:
![]() $[V]^{\leq \omega }$
are the sets of rank
$[V]^{\leq \omega }$
are the sets of rank
![]() $0$
, the successor steps are countable union of sets from previous ranks, and the limit steps are unions of previous ranks. As we remarked, in Gitik’s model, every set has a rank in that sense.
$0$
, the successor steps are countable union of sets from previous ranks, and the limit steps are unions of previous ranks. As we remarked, in Gitik’s model, every set has a rank in that sense.
By induction on this rank, if A is a least ranked set which has a fresh subset, B, in a generic extension, let
![]() $\{A_n\mid n<\omega \}$
be a countable sequence of sets of lower rank whose union is A, then either
$\{A_n\mid n<\omega \}$
be a countable sequence of sets of lower rank whose union is A, then either
![]() $\{A_n\cap B\mid n<\omega \}$
is a fresh sequence, or
$\{A_n\cap B\mid n<\omega \}$
is a fresh sequence, or
![]() $B\cap A_n$
is fresh for some
$B\cap A_n$
is fresh for some
![]() $n<\omega $
. Since A is minimally ranked, the latter is impossible, and so the generic extension must not be
$n<\omega $
. Since A is minimally ranked, the latter is impossible, and so the generic extension must not be
![]() $\sigma $
-sequential.
$\sigma $
-sequential.
Next, since every infinite set is a countable union of sets of smaller cardinality, every infinite set can be mapped onto
![]() $\omega $
. So, by
$\omega $
. So, by
![]() $*$
-closure of
$*$
-closure of
![]() $ \mathcal S_{\mathbb P}$
, if X is infinite and
$ \mathcal S_{\mathbb P}$
, if X is infinite and
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\leq }|X|$
-sequential, then
${\leq }|X|$
-sequential, then
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\sigma $
-sequential, and thus trivial.
$\sigma $
-sequential, and thus trivial.
4 Some minor positive results about distributive forcings
Theorem 4.1 Suppose that
![]() $\mathsf {AC}_X$
holds, if
$\mathsf {AC}_X$
holds, if
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\leq }|X|$
-distributive, then
${\leq }|X|$
-distributive, then
![]() $\mathsf {AC}_X$
is preserved.
$\mathsf {AC}_X$
is preserved.
Proof Suppose that
![]() $\dot F$
is a
$\dot F$
is a
![]() ${\mathbb P}$
-name and
${\mathbb P}$
-name and
![]() is a function with domain
is a function with domain
![]() $\check X$
and
$\check X$
and
![]() $\dot F(\check x)\neq \check \varnothing $
for all
$\dot F(\check x)\neq \check \varnothing $
for all
![]() $x\in X$
.” For each
$x\in X$
.” For each
![]() $x\in X$
, let
$x\in X$
, let
![]() $D_x$
be the dense open set
$D_x$
be the dense open set
![]() $\{p\in {\mathbb P}\mid \exists \dot y(p\mathrel {\Vdash }\dot y\in \dot F(\check x))\}$
. Suppose that
$\{p\in {\mathbb P}\mid \exists \dot y(p\mathrel {\Vdash }\dot y\in \dot F(\check x))\}$
. Suppose that
![]() $p\in \bigcap _{x\in X}D_x$
, then for all
$p\in \bigcap _{x\in X}D_x$
, then for all
![]() $x\in X$
the class
$x\in X$
the class
![]() $\{\dot y\in V^{\mathbb P}\mid p\mathrel {\Vdash }\dot y\in \dot F(\check x)\}$
is nonempty. Using Scott’s trick, we may assume that each of these is a set. Applying
$\{\dot y\in V^{\mathbb P}\mid p\mathrel {\Vdash }\dot y\in \dot F(\check x)\}$
is nonempty. Using Scott’s trick, we may assume that each of these is a set. Applying
![]() $\mathsf {AC}_X$
in V, there is a function f such that for all
$\mathsf {AC}_X$
in V, there is a function f such that for all
![]() $x\in X$
,
$x\in X$
,
![]() $f(x)=\dot y$
and
$f(x)=\dot y$
and
![]() $p\mathrel {\Vdash }\dot y\in \dot F(\check x)$
. This lets us define an obvious name for a choice function below p.
$p\mathrel {\Vdash }\dot y\in \dot F(\check x)$
. This lets us define an obvious name for a choice function below p.
Since
![]() $\bigcap _{x\in X}D_x$
is dense,
$\bigcap _{x\in X}D_x$
is dense,
![]() as wanted.
as wanted.
Proposition 4.2 If
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() ${\leq }|X|$
-sequential and
${\leq }|X|$
-sequential and
![]() $\mathrel {\Vdash }_{\mathbb P}\mathsf {AC}_X$
, then
$\mathrel {\Vdash }_{\mathbb P}\mathsf {AC}_X$
, then
![]() $\mathsf {AC}_X$
holds in V.
$\mathsf {AC}_X$
holds in V.
If we concentrate on the case where
![]() $X=\omega $
, this shows that a
$X=\omega $
, this shows that a
![]() $\sigma $
-distributive must preserve
$\sigma $
-distributive must preserve
![]() $\mathsf {AC}_{\omega }$
. From the work of the first author with Asperó in [Reference Asperó and Karagila1] we know that a proper forcing, and in particular a
$\mathsf {AC}_{\omega }$
. From the work of the first author with Asperó in [Reference Asperó and Karagila1] we know that a proper forcing, and in particular a
![]() $\sigma $
-closed forcing,Footnote
11
must preserve
$\sigma $
-closed forcing,Footnote
11
must preserve
![]() $\mathsf {DC}$
, so the natural question now is: does
$\mathsf {DC}$
, so the natural question now is: does
![]() $\sigma $
-distributive suffice for the proof?
$\sigma $
-distributive suffice for the proof?
There are reasons to expect a positive answer. For example, assuming
![]() $\mathsf {AC}$
holds, if
$\mathsf {AC}$
holds, if
![]() $\langle {\mathbb P},\mathscr {G},\mathscr {F}\rangle $
is a symmetric system where
$\langle {\mathbb P},\mathscr {G},\mathscr {F}\rangle $
is a symmetric system where
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\sigma $
-distributive and
$\sigma $
-distributive and
![]() $\mathscr {F}$
is
$\mathscr {F}$
is
![]() $\sigma $
-complete, then
$\sigma $
-complete, then
![]() $\mathsf {DC}$
holds in the symmetric extension (see, for example, [Reference Banerjee2, Reference Karagila and Schilhan9]). As the main theorem of this paper shows, however, this is not the case in
$\mathsf {DC}$
holds in the symmetric extension (see, for example, [Reference Banerjee2, Reference Karagila and Schilhan9]). As the main theorem of this paper shows, however, this is not the case in
![]() $\mathsf {ZF}$
. One is left asking, is there a property between
$\mathsf {ZF}$
. One is left asking, is there a property between
![]() $\sigma $
-distributive and proper which preserves
$\sigma $
-distributive and proper which preserves
![]() $\mathsf {DC}$
?
$\mathsf {DC}$
?
Definition 4.3 We say that a forcing
![]() ${\mathbb P}$
is quasiproper if for every
${\mathbb P}$
is quasiproper if for every
![]() $p\in {\mathbb P}$
and
$p\in {\mathbb P}$
and
![]() ${\mathbb P}$
-name
${\mathbb P}$
-name
![]() $\dot X$
there is a countable elementary submodel, M, of some large enough
$\dot X$
there is a countable elementary submodel, M, of some large enough
![]() $H(\kappa )$
such that
$H(\kappa )$
such that
![]() $p,{\mathbb P},\dot X\in M$
and there is some
$p,{\mathbb P},\dot X\in M$
and there is some
![]() $q\leq p$
such that q is an M-generic condition. Namely, every dense open set
$q\leq p$
such that q is an M-generic condition. Namely, every dense open set
![]() $D\in M$
is predense below q.
$D\in M$
is predense below q.
Note that the model M depends very much on the choice of p and
![]() $\dot X$
. So quasiproperness is still far from properness. We follow [Reference Asperó and Karagila1] and define
$\dot X$
. So quasiproperness is still far from properness. We follow [Reference Asperó and Karagila1] and define
![]() $H(\kappa )$
to be
$H(\kappa )$
to be
![]() $\{x\mid \kappa \nleq ^*|\operatorname {\mathrm {tcl}}(\{x\})|\}$
, but we can just as well work with
$\{x\mid \kappa \nleq ^*|\operatorname {\mathrm {tcl}}(\{x\})|\}$
, but we can just as well work with
![]() $V_{\alpha }$
for a large enough limit ordinal
$V_{\alpha }$
for a large enough limit ordinal
![]() $\alpha $
for all intents and purposes.
$\alpha $
for all intents and purposes.
Theorem 4.4 (
 $\mathsf {ZF}+\mathsf {DC}$
)
$\mathsf {ZF}+\mathsf {DC}$
)
Let
![]() ${\mathbb P}$
be a forcing notion. If
${\mathbb P}$
be a forcing notion. If
![]() ${\mathbb P}$
is quasiproper, then it preserves
${\mathbb P}$
is quasiproper, then it preserves
![]() $\mathsf {DC}$
. If
$\mathsf {DC}$
. If
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\sigma $
-sequential and preserves
$\sigma $
-sequential and preserves
![]() $\mathsf {DC}$
, then
$\mathsf {DC}$
, then
![]() ${\mathbb P}$
is quasiproper.
${\mathbb P}$
is quasiproper.
Proof The core of the first part of the theorem is the same proof as Theorem 4.6 from [Reference Asperó and Karagila1], suppose that
![]() $\dot T$
is a name for a tree without maximal nodes, then for every p there is some suitable model, M and an M-generic
$\dot T$
is a name for a tree without maximal nodes, then for every p there is some suitable model, M and an M-generic
![]() $q\leq p$
. Note that if q is M-generic, then
$q\leq p$
. Note that if q is M-generic, then
![]() $q\mathrel {\Vdash }"\dot T\cap M$
is a countable subtree of
$q\mathrel {\Vdash }"\dot T\cap M$
is a countable subtree of
![]() $\dot T$
without maximal nodes,” and so q forces that
$\dot T$
without maximal nodes,” and so q forces that
![]() $\dot T$
must have a branch. But the above just means that the set of conditions q which are M-generic for some suitable M is dense, which guarantees that
$\dot T$
must have a branch. But the above just means that the set of conditions q which are M-generic for some suitable M is dense, which guarantees that
![]() $\dot T$
is forced to have a branch, and therefore
$\dot T$
is forced to have a branch, and therefore
![]() $\mathsf {DC}$
is preserved.
$\mathsf {DC}$
is preserved.
For the second part, suppose that
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\sigma $
-sequential and that
$\sigma $
-sequential and that
![]() $\mathsf {DC}$
is preserved. Fix any
$\mathsf {DC}$
is preserved. Fix any
![]() $p,\dot X$
in V, fix a large enough
$p,\dot X$
in V, fix a large enough
![]() $\kappa $
and consider the set
$\kappa $
and consider the set
![]() $ \mathcal M$
of countable elementary submodels of
$ \mathcal M$
of countable elementary submodels of
![]() $H(\kappa )$
which contain
$H(\kappa )$
which contain
![]() $p,{\mathbb P}$
and
$p,{\mathbb P}$
and
![]() $\dot X$
. Working in
$\dot X$
. Working in
![]() $V[G]$
, where G is V-generic with
$V[G]$
, where G is V-generic with
![]() $p\in G$
, we define a relation on
$p\in G$
, we define a relation on
![]() $ \mathcal M$
:
$ \mathcal M$
:
![]() $M\sqsubset N$
if and only if:
$M\sqsubset N$
if and only if:
-
(1) N is an elementary extension of M.
-
(2)
 $G\cap N\cap D\neq \varnothing $
for every dense open
$G\cap N\cap D\neq \varnothing $
for every dense open
 $D\in M$
.
$D\in M$
.
We first show that if
![]() $M\in \mathcal M$
, then there is some
$M\in \mathcal M$
, then there is some
![]() $N\in \mathcal M$
such that
$N\in \mathcal M$
such that
![]() $M\sqsubset N$
. Let M be such model, then we can enumerate all the dense open sets in M as
$M\sqsubset N$
. Let M be such model, then we can enumerate all the dense open sets in M as
![]() $\{D_n\mid n<\omega \}$
and using
$\{D_n\mid n<\omega \}$
and using
![]() $\mathsf {DC}$
there is a sequence of conditions
$\mathsf {DC}$
there is a sequence of conditions
![]() $p_n\in G\cap D_n$
for all
$p_n\in G\cap D_n$
for all
![]() $n<\omega $
. The sequence
$n<\omega $
. The sequence
![]() $\langle p_n\mid n<\omega \rangle $
lies in the ground model, since
$\langle p_n\mid n<\omega \rangle $
lies in the ground model, since
![]() ${\mathbb P}$
is
${\mathbb P}$
is
![]() $\sigma $
-sequential.
$\sigma $
-sequential.
![]() $\mathsf {DC}$
implies that there is an elementary submodel in
$\mathsf {DC}$
implies that there is an elementary submodel in
![]() $ \mathcal M$
generated by adding
$ \mathcal M$
generated by adding
![]() $\{p_n\mid n<\omega \}$
to M.
$\{p_n\mid n<\omega \}$
to M.
Employing
![]() $\mathsf {DC}$
in
$\mathsf {DC}$
in
![]() $V[G]$
, we have a sequence of models
$V[G]$
, we have a sequence of models
![]() $\langle M_n\mid n<\omega \rangle $
such that
$\langle M_n\mid n<\omega \rangle $
such that
![]() $M_n\sqsubset M_{n+1}$
for all n. This sequence is again in V, and its union
$M_n\sqsubset M_{n+1}$
for all n. This sequence is again in V, and its union
![]() $M=\bigcup M_n$
, is a countable elementary submodel of
$M=\bigcup M_n$
, is a countable elementary submodel of
![]() $H(\kappa )$
. In
$H(\kappa )$
. In
![]() $V[G]$
, we have that for every dense open
$V[G]$
, we have that for every dense open
![]() $D\in M$
,
$D\in M$
,
![]() $D\cap M\cap G\neq \varnothing $
: if
$D\cap M\cap G\neq \varnothing $
: if
![]() $D\in M$
, then
$D\in M$
, then
![]() $D\in M_n$
for some n, and therefore in
$D\in M_n$
for some n, and therefore in
![]() $M_{n+1}$
there is a condition in
$M_{n+1}$
there is a condition in
![]() $D\cap G\cap M_{n+1}$
. Therefore there is some
$D\cap G\cap M_{n+1}$
. Therefore there is some
![]() $q\leq p$
which is M-generic as wanted.
$q\leq p$
which is M-generic as wanted.
5 Main results
Theorem 5.1 Let
![]() $\kappa $
be any infinite cardinal. It is consistent with
$\kappa $
be any infinite cardinal. It is consistent with
![]() $\mathsf {ZF}+\mathsf {DC}_{<\kappa }$
that:
$\mathsf {ZF}+\mathsf {DC}_{<\kappa }$
that:
-
(1) There is a
 $\kappa $
-distributive forcing which violates
$\kappa $
-distributive forcing which violates
 $\mathsf {DC}$
.
$\mathsf {DC}$
. -
(2) There is a
 $\kappa $
-sequential forcing which violates
$\kappa $
-sequential forcing which violates
 $\mathsf {AC}_{\omega }$
.
$\mathsf {AC}_{\omega }$
.
Proof Let
![]() $\kappa $
be an uncountable regular cardinal and consider the
$\kappa $
be an uncountable regular cardinal and consider the
![]() $\kappa $
-Cohen model, as described in Example 2.1. The case of
$\kappa $
-Cohen model, as described in Example 2.1. The case of
![]() $\kappa =\omega $
is vacuously true since
$\kappa =\omega $
is vacuously true since
![]() $\mathsf {AC}_{\omega }$
already fails in the Cohen model. Denote by M the symmetric extension, and by
$\mathsf {AC}_{\omega }$
already fails in the Cohen model. Denote by M the symmetric extension, and by
![]() $\langle {\mathbb P},\mathscr {G},\mathscr {F}\rangle $
the symmetric system. As usual, we will omit the dots from names to denote their interpretation in M.
$\langle {\mathbb P},\mathscr {G},\mathscr {F}\rangle $
the symmetric system. As usual, we will omit the dots from names to denote their interpretation in M.
As explained in the above example,
![]() $M\models \mathsf {DC}_{<\kappa }$
. We will describe two partial orders in this model which will witness the two failures. The first partial order will add a tree structure on A which will witness the failure of
$M\models \mathsf {DC}_{<\kappa }$
. We will describe two partial orders in this model which will witness the two failures. The first partial order will add a tree structure on A which will witness the failure of
![]() $\mathsf {DC}$
, the second will add an amorphous partition.Footnote
12
In both cases, the idea is to consider the natural symmetric system which adds these objects “directly” and factor it into these two steps: first, a symmetric extension adding a set of subsets of
$\mathsf {DC}$
, the second will add an amorphous partition.Footnote
12
In both cases, the idea is to consider the natural symmetric system which adds these objects “directly” and factor it into these two steps: first, a symmetric extension adding a set of subsets of
![]() $\kappa $
, then add the structure that would naturally be added by the “direct” symmetric extension.
$\kappa $
, then add the structure that would naturally be added by the “direct” symmetric extension.
Working in
![]() $M,$
let
$M,$
let
![]() $\mathbb Q_0$
be the partial order given by all the well-orderable and well-founded trees on A,Footnote
13
ordered by
$\mathbb Q_0$
be the partial order given by all the well-orderable and well-founded trees on A,Footnote
13
ordered by
![]() $t_1\leq t_0$
if and only if
$t_1\leq t_0$
if and only if
![]() $t_0$
is downward closed in
$t_0$
is downward closed in
![]() $t_1$
. We claim that first of all,
$t_1$
. We claim that first of all,
![]() $\mathbb Q_0$
is
$\mathbb Q_0$
is
![]() $\kappa $
-distributive, and secondly if
$\kappa $
-distributive, and secondly if
![]() $H\subseteq \mathbb Q_0$
is M-generic, H defines a tree on A which is of height
$H\subseteq \mathbb Q_0$
is M-generic, H defines a tree on A which is of height
![]() $\omega $
, without maximal nodes, and without branches, witnessing that
$\omega $
, without maximal nodes, and without branches, witnessing that
![]() $\mathsf {DC}$
fails in
$\mathsf {DC}$
fails in
![]() $M[H]$
.
$M[H]$
.
First, we note that if
![]() $t\in \mathbb Q_0$
, then t has a canonical
$t\in \mathbb Q_0$
, then t has a canonical
![]() ${\mathbb P}$
-name in
${\mathbb P}$
-name in
![]() $\mathsf {HS}$
. Since we are not adding any sets of size
$\mathsf {HS}$
. Since we are not adding any sets of size
![]() $<\kappa $
to V, therefore there is some
$<\kappa $
to V, therefore there is some
![]() $T\in V$
which is a well-founded tree on a bounded subset of
$T\in V$
which is a well-founded tree on a bounded subset of
![]() $\kappa $
, and
$\kappa $
, and
![]() $\dot t=\{\langle \dot a_{\alpha },\dot a_{\beta }\rangle ^{\bullet }\mid \langle \alpha ,\beta \rangle \in T\}^{\bullet }$
is a
$\dot t=\{\langle \dot a_{\alpha },\dot a_{\beta }\rangle ^{\bullet }\mid \langle \alpha ,\beta \rangle \in T\}^{\bullet }$
is a
![]() ${\mathbb P}$
-name for t. We will use T and
${\mathbb P}$
-name for t. We will use T and
![]() $\dot t$
to correspond between this tree and the condition in
$\dot t$
to correspond between this tree and the condition in
![]() $\mathbb Q_0$
, and because of this canonicity, there is no confusion when we treat them interchangeably where appropriate.
$\mathbb Q_0$
, and because of this canonicity, there is no confusion when we treat them interchangeably where appropriate.
Let
![]() $\gamma <\kappa ,$
and let
$\gamma <\kappa ,$
and let
![]() $\langle D_{\alpha }\mid \alpha <\gamma \rangle \in M$
be a sequence of dense open subsets of
$\langle D_{\alpha }\mid \alpha <\gamma \rangle \in M$
be a sequence of dense open subsets of
![]() $\mathbb Q_0$
. This sequence has a name in
$\mathbb Q_0$
. This sequence has a name in
![]() $\mathsf {HS}$
, and since
$\mathsf {HS}$
, and since
![]() $\mathscr {F}$
is
$\mathscr {F}$
is
![]() $\kappa $
-complete, we can simply choose names
$\kappa $
-complete, we can simply choose names
![]() $\dot D_{\alpha }$
for each
$\dot D_{\alpha }$
for each
![]() $\alpha <\gamma $
and consider
$\alpha <\gamma $
and consider
![]() $\langle \dot D_{\alpha }\mid \alpha <\gamma \rangle ^{\bullet }$
as our canonical name.
$\langle \dot D_{\alpha }\mid \alpha <\gamma \rangle ^{\bullet }$
as our canonical name.
Let p be a fixed condition in
![]() ${\mathbb P}$
which forces that each
${\mathbb P}$
which forces that each
![]() $\dot D_{\alpha }$
is a dense open set, and let
$\dot D_{\alpha }$
is a dense open set, and let
![]() $\dot t$
be a canonical name for a condition. Fix E such that
$\dot t$
be a canonical name for a condition. Fix E such that
![]() $\operatorname {\mathrm {supp}} p,\operatorname {\mathrm {sym}}(\dot t)$
, and for all
$\operatorname {\mathrm {supp}} p,\operatorname {\mathrm {sym}}(\dot t)$
, and for all
![]() $\alpha $
,
$\alpha $
,
![]() $\operatorname {\mathrm {sym}}(\dot D_{\alpha })$
all contain
$\operatorname {\mathrm {sym}}(\dot D_{\alpha })$
all contain
![]() $\operatorname {\mathrm {fix}}(E)$
. We may even assume, without loss of generality that
$\operatorname {\mathrm {fix}}(E)$
. We may even assume, without loss of generality that
![]() $\operatorname {\mathrm {dom}} T=E$
, else we can simply extend
$\operatorname {\mathrm {dom}} T=E$
, else we can simply extend
![]() $\dot t$
as necessary.
$\dot t$
as necessary.
Let
![]() $p'\leq p$
be a condition such that for each
$p'\leq p$
be a condition such that for each
![]() $\alpha <\gamma $
, there is some canonical
$\alpha <\gamma $
, there is some canonical
![]() $\dot t_{\alpha }$
such that
$\dot t_{\alpha }$
such that
![]() $p'\mathrel {\Vdash }\dot t_{\alpha }\in \dot D_{\alpha }$
and
$p'\mathrel {\Vdash }\dot t_{\alpha }\in \dot D_{\alpha }$
and
![]() $\dot t\subseteq \dot t_{\alpha }$
.Footnote
14
Let
$\dot t\subseteq \dot t_{\alpha }$
.Footnote
14
Let
![]() $E'$
be a large enough set such that
$E'$
be a large enough set such that
![]() $\operatorname {\mathrm {fix}}(E')\subseteq \operatorname {\mathrm {sym}}(\dot t_{\alpha })$
for all
$\operatorname {\mathrm {fix}}(E')\subseteq \operatorname {\mathrm {sym}}(\dot t_{\alpha })$
for all
![]() $\alpha <\gamma $
, and
$\alpha <\gamma $
, and
![]() $E\cup \operatorname {\mathrm {supp}} p'\subseteq E'$
. Such
$E\cup \operatorname {\mathrm {supp}} p'\subseteq E'$
. Such
![]() $E'$
exists since
$E'$
exists since
![]() $\kappa $
is regular and
$\kappa $
is regular and
![]() $\gamma <\kappa $
.
$\gamma <\kappa $
.
For each
![]() $\alpha <\gamma $
, pick
$\alpha <\gamma $
, pick
![]() $\pi _{\alpha }\colon \kappa \to \kappa $
to be a permutation such that
$\pi _{\alpha }\colon \kappa \to \kappa $
to be a permutation such that
![]() $\pi _{\alpha }\in \operatorname {\mathrm {fix}}(E)$
, and letting
$\pi _{\alpha }\in \operatorname {\mathrm {fix}}(E)$
, and letting
![]() $\pi _{\alpha }"(E'\setminus E)=E_{\alpha }$
,” we have that
$\pi _{\alpha }"(E'\setminus E)=E_{\alpha }$
,” we have that
![]() $\{E_{\alpha }\mid \alpha <\gamma \}$
are all pairwise disjoint. These exist since
$\{E_{\alpha }\mid \alpha <\gamma \}$
are all pairwise disjoint. These exist since
![]() $|E'|<\kappa $
. Observe the following:
$|E'|<\kappa $
. Observe the following:
-
(1)
 $q=\bigcup _{\alpha <\gamma }\pi _{\alpha } p'$
is a condition, since
$q=\bigcup _{\alpha <\gamma }\pi _{\alpha } p'$
is a condition, since
 $\operatorname {\mathrm {dom}}\pi _{\alpha } p'\cap \operatorname {\mathrm {dom}}\pi _{\beta } p'=E$
.
$\operatorname {\mathrm {dom}}\pi _{\alpha } p'\cap \operatorname {\mathrm {dom}}\pi _{\beta } p'=E$
. -
(2)
 $\pi _{\alpha } p'\mathrel {\Vdash }\pi _{\alpha }\dot t_{\alpha }\in \dot D_{\alpha }$
and
$\pi _{\alpha } p'\mathrel {\Vdash }\pi _{\alpha }\dot t_{\alpha }\in \dot D_{\alpha }$
and
 $\dot t\subseteq \pi \dot t_{\alpha }$
.
$\dot t\subseteq \pi \dot t_{\alpha }$
. -
(3) If
 $\xi \in \operatorname {\mathrm {dom}}\pi _{\alpha } T_{\alpha }\cap \operatorname {\mathrm {dom}}\pi _{\beta } T_{\beta }$
for any
$\xi \in \operatorname {\mathrm {dom}}\pi _{\alpha } T_{\alpha }\cap \operatorname {\mathrm {dom}}\pi _{\beta } T_{\beta }$
for any
 $\alpha \neq \beta $
, then
$\alpha \neq \beta $
, then
 $\xi \in E$
.
$\xi \in E$
.
It follows from the three conditions that setting
![]() $\dot s=\bigcup _{\alpha <\gamma }\pi _{\alpha }\dot t_{\alpha }$
is a condition. If it were not a tree then any pair witnessing this must be already in
$\dot s=\bigcup _{\alpha <\gamma }\pi _{\alpha }\dot t_{\alpha }$
is a condition. If it were not a tree then any pair witnessing this must be already in
![]() $\dot t$
itself, by the third condition, which is impossible. Similarly, if
$\dot t$
itself, by the third condition, which is impossible. Similarly, if
![]() $\dot s$
is not well-founded, then by the third condition it means some
$\dot s$
is not well-founded, then by the third condition it means some
![]() $\dot t_{\alpha }$
was not well-founded.
$\dot t_{\alpha }$
was not well-founded.
But this means that
![]() $q\mathrel {\Vdash }\dot s\in \dot D_{\alpha }$
for all
$q\mathrel {\Vdash }\dot s\in \dot D_{\alpha }$
for all
![]() $\alpha $
. So given any p and
$\alpha $
. So given any p and
![]() $\dot t$
, we can extend p to q and find
$\dot t$
, we can extend p to q and find
![]() $\dot s$
such that
$\dot s$
such that
![]() $q\mathrel {\Vdash }\dot t\subseteq \dot s\in \dot D_{\alpha }$
for all
$q\mathrel {\Vdash }\dot t\subseteq \dot s\in \dot D_{\alpha }$
for all
![]() $\alpha $
, and therefore the intersection of the
$\alpha $
, and therefore the intersection of the
![]() $D_{\alpha }$
is dense.
$D_{\alpha }$
is dense.
Next, it is easy to see that if
![]() $H\subseteq \mathbb Q_0$
is M-generic, then
$H\subseteq \mathbb Q_0$
is M-generic, then
![]() $T=\bigcup H$
defines a tree structure on A. Standard density arguments show that this tree has height
$T=\bigcup H$
defines a tree structure on A. Standard density arguments show that this tree has height
![]() $\omega $
and no maximal elements. Finally, since
$\omega $
and no maximal elements. Finally, since
![]() $\mathbb Q_0$
is
$\mathbb Q_0$
is
![]() $\sigma $
-distributive, it adds no new
$\sigma $
-distributive, it adds no new
![]() $\omega $
-sequence. So it is enough to show that if
$\omega $
-sequence. So it is enough to show that if
![]() $\{a_n\mid n<\omega \}\subseteq A$
is in M, then it is not a branch in T. But this is again a simple density argument, given any condition t, pick any point in t, and whatever
$\{a_n\mid n<\omega \}\subseteq A$
is in M, then it is not a branch in T. But this is again a simple density argument, given any condition t, pick any point in t, and whatever
![]() $a_n$
s are not already mentioned in t, add as immediate successors of the chosen point. Therefore, by density argument no ground model set is a branch, and so T is indeed without branches and serves as a counterexample to
$a_n$
s are not already mentioned in t, add as immediate successors of the chosen point. Therefore, by density argument no ground model set is a branch, and so T is indeed without branches and serves as a counterexample to
![]() $\mathsf {DC}$
.Footnote
15
$\mathsf {DC}$
.Footnote
15
Indeed, this is the essence of the standard proof that
![]() $\mathsf {AC}_{<\kappa }$
does not imply
$\mathsf {AC}_{<\kappa }$
does not imply
![]() $\mathsf {DC}$
: first force with
$\mathsf {DC}$
: first force with
![]() $\operatorname {\mathrm {Add}}(\kappa ,\kappa ^{<\omega })$
, take the automorphism group of the tree
$\operatorname {\mathrm {Add}}(\kappa ,\kappa ^{<\omega })$
, take the automorphism group of the tree
![]() $\kappa ^{<\omega }$
and generate the supports by fixing well-founded trees of rank
$\kappa ^{<\omega }$
and generate the supports by fixing well-founded trees of rank
![]() $<\kappa $
. See Theorem 8.12 in [Reference Jech6] for a similar construction in the context of permutation models.
$<\kappa $
. See Theorem 8.12 in [Reference Jech6] for a similar construction in the context of permutation models.
For the second partial order, let
![]() $\mathbb Q_1$
be the partial order given by finite partitions of well-orderable subsets of A. Namely, a condition is a finite set, e, consisting of pairwise disjoint well-orderable subsets of A.
$\mathbb Q_1$
be the partial order given by finite partitions of well-orderable subsets of A. Namely, a condition is a finite set, e, consisting of pairwise disjoint well-orderable subsets of A.
We will denote
![]() $\bigcup e$
as
$\bigcup e$
as
![]() $\operatorname {\mathrm {dom}} e$
, and given
$\operatorname {\mathrm {dom}} e$
, and given
![]() $a\in A$
, we will write
$a\in A$
, we will write
![]() $e(a)$
to denote the cell containing a, which may be empty if
$e(a)$
to denote the cell containing a, which may be empty if
![]() $a\notin \operatorname {\mathrm {dom}} e$
. Given some
$a\notin \operatorname {\mathrm {dom}} e$
. Given some
![]() $A'\subseteq A$
, we will also write
$A'\subseteq A$
, we will also write
![]() $e\mathbin \upharpoonright A'=\{C\cap A'\mid C\in e\}$
.
$e\mathbin \upharpoonright A'=\{C\cap A'\mid C\in e\}$
.
We define the order by
![]() $e_2\leq _{\mathbb Q_1} e_1$
if and only if
$e_2\leq _{\mathbb Q_1} e_1$
if and only if
![]() $e_2\mathbin \upharpoonright \operatorname {\mathrm {dom}} e_1=e_1$
. In other words,
$e_2\mathbin \upharpoonright \operatorname {\mathrm {dom}} e_1=e_1$
. In other words,
![]() $e_2$
can extend the cells of
$e_2$
can extend the cells of
![]() $e_1$
or adds new ones, but it not merge any distinct cells.
$e_1$
or adds new ones, but it not merge any distinct cells.
We need to show that
![]() $\mathbb Q_1$
is
$\mathbb Q_1$
is
![]() $\kappa $
-sequential and that if
$\kappa $
-sequential and that if
![]() $H\subseteq \mathbb Q_1$
is M-generic, then
$H\subseteq \mathbb Q_1$
is M-generic, then
![]() $\bigcup H$
is an amorphous partition of A. This will show that
$\bigcup H$
is an amorphous partition of A. This will show that
![]() $M[H]\models \lnot \mathsf {AC}_{\omega }$
, as wanted. Note that
$M[H]\models \lnot \mathsf {AC}_{\omega }$
, as wanted. Note that
![]() $\mathbb Q_1$
is not even
$\mathbb Q_1$
is not even
![]() $\sigma $
-distributive by considering
$\sigma $
-distributive by considering
![]() $D_n=\{e\in \mathbb Q_1\mid n\leq |e|\}$
.
$D_n=\{e\in \mathbb Q_1\mid n\leq |e|\}$
.
Note if
![]() $e\in \mathbb Q_1$
, then there is finite partition E of some bounded subset of
$e\in \mathbb Q_1$
, then there is finite partition E of some bounded subset of
![]() $\kappa $
such that
$\kappa $
such that
![]() $\dot e=\{\{\dot a_{\alpha }\mid \alpha \in C\}^{\bullet }\mid C\in E\}^{\bullet }$
is a name for e. We will adopt a similar convention to the previous case, that E is the finite partition defining
$\dot e=\{\{\dot a_{\alpha }\mid \alpha \in C\}^{\bullet }\mid C\in E\}^{\bullet }$
is a name for e. We will adopt a similar convention to the previous case, that E is the finite partition defining
![]() $\dot e$
and vice versa. Furthermore, when it will be clear from context, we may also conflate E and
$\dot e$
and vice versa. Furthermore, when it will be clear from context, we may also conflate E and
![]() $\dot e$
to simplify the text, so if
$\dot e$
to simplify the text, so if
![]() $S\subseteq \kappa $
, the meaning of
$S\subseteq \kappa $
, the meaning of
![]() $\dot e\mathbin \upharpoonright S$
is clear: it is the condition corresponding to
$\dot e\mathbin \upharpoonright S$
is clear: it is the condition corresponding to
![]() $E\mathbin \upharpoonright S$
.
$E\mathbin \upharpoonright S$
.
One important consequence of the existence of these canonical names is that
![]() $\mathbb Q_1$
, as an ordered set, has a canonical name that is stable under all the automorphisms in
$\mathbb Q_1$
, as an ordered set, has a canonical name that is stable under all the automorphisms in
![]() $\mathscr {G}$
. This means that we can apply
$\mathscr {G}$
. This means that we can apply
![]() $\pi \in \mathscr {G}$
to statements of the form
$\pi \in \mathscr {G}$
to statements of the form
![]() $p\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e\mathrel {\Vdash }_{\mathbb Q_1}\varphi $
without having to worry that
$p\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e\mathrel {\Vdash }_{\mathbb Q_1}\varphi $
without having to worry that
![]() $\pi $
will somehow change the meaning of
$\pi $
will somehow change the meaning of
![]() $\mathrel {\Vdash }_{\mathbb Q_1}$
.
$\mathrel {\Vdash }_{\mathbb Q_1}$
.
Suppose that
![]() $\dot f\in M$
is a
$\dot f\in M$
is a
![]() $\mathbb Q_1$
-name for a new
$\mathbb Q_1$
-name for a new
![]() $\gamma $
-sequence of elements of M, for some
$\gamma $
-sequence of elements of M, for some
![]() $\gamma <\kappa $
. We may assume, without loss of generality, that every name appearing in
$\gamma <\kappa $
. We may assume, without loss of generality, that every name appearing in
![]() $\dot f$
is of the form
$\dot f$
is of the form
![]() $\langle \check \alpha ,\check x\rangle ^{\bullet }$
for some
$\langle \check \alpha ,\check x\rangle ^{\bullet }$
for some
![]() $x\in M$
. Let
$x\in M$
. Let
![]() $[\dot f]\in \mathsf {HS}$
be a
$[\dot f]\in \mathsf {HS}$
be a
![]() ${\mathbb P}$
-name for
${\mathbb P}$
-name for
![]() $\dot f$
, for example, one such that every name that appears in it has the form
$\dot f$
, for example, one such that every name that appears in it has the form
![]() $\langle \dot e,\langle \check \alpha ,\dot x\rangle ^{\bullet }\rangle ^{\bullet }$
, where
$\langle \dot e,\langle \check \alpha ,\dot x\rangle ^{\bullet }\rangle ^{\bullet }$
, where
![]() $\dot e$
is some canonical name for a condition in
$\dot e$
is some canonical name for a condition in
![]() $\mathbb Q_1$
and
$\mathbb Q_1$
and
![]() $\dot x$
is a name in
$\dot x$
is a name in
![]() $\mathsf {HS}$
for the canonical
$\mathsf {HS}$
for the canonical
![]() $\mathbb Q_1$
-name,
$\mathbb Q_1$
-name,
![]() $\check x$
, in M.
$\check x$
, in M.
Let
![]() $S\in [\kappa ]^{<\kappa }$
such that
$S\in [\kappa ]^{<\kappa }$
such that
![]() $\operatorname {\mathrm {fix}}(S)\subseteq \operatorname {\mathrm {sym}}([\dot f])$
. Let
$\operatorname {\mathrm {fix}}(S)\subseteq \operatorname {\mathrm {sym}}([\dot f])$
. Let
![]() $p\in {\mathbb P}$
be any condition such that
$p\in {\mathbb P}$
be any condition such that
![]() $p\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e\mathrel {\Vdash }_{\mathbb Q_1}[\dot f](\check \alpha )=\dot x$
for some
$p\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e\mathrel {\Vdash }_{\mathbb Q_1}[\dot f](\check \alpha )=\dot x$
for some
![]() $\dot e$
and
$\dot e$
and
![]() $\alpha <\gamma $
.
$\alpha <\gamma $
.
Claim 5.2
![]() $p\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e\mathbin \upharpoonright S\mathrel {\Vdash }_{\mathbb Q_1}[\dot f](\check \alpha )=\dot x$
.
$p\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e\mathbin \upharpoonright S\mathrel {\Vdash }_{\mathbb Q_1}[\dot f](\check \alpha )=\dot x$
.
Proof (Claim)
Suppose that
![]() $\dot e'$
is a name for a condition extending
$\dot e'$
is a name for a condition extending
![]() $\dot e\mathbin \upharpoonright S$
. We can find
$\dot e\mathbin \upharpoonright S$
. We can find
![]() $\pi \in \operatorname {\mathrm {fix}}(S)$
such that
$\pi \in \operatorname {\mathrm {fix}}(S)$
such that
![]() $\pi p$
is compatible with p and
$\pi p$
is compatible with p and
![]() $\pi \dot e$
is compatible with both
$\pi \dot e$
is compatible with both
![]() $\dot e$
and
$\dot e$
and
![]() $\dot e'$
by mapping
$\dot e'$
by mapping
![]() $\operatorname {\mathrm {dom}}\dot e\backslash S$
and
$\operatorname {\mathrm {dom}}\dot e\backslash S$
and
![]() $\operatorname {\mathrm {supp}} p\backslash S$
“far enough” from
$\operatorname {\mathrm {supp}} p\backslash S$
“far enough” from
![]() $\operatorname {\mathrm {dom}}\dot e'$
and
$\operatorname {\mathrm {dom}}\dot e'$
and
![]() $\operatorname {\mathrm {supp}} p$
. Then we have that
$\operatorname {\mathrm {supp}} p$
. Then we have that
Since
![]() $\pi p$
and p are compatible, we can set
$\pi p$
and p are compatible, we can set
![]() $q=p\cup \pi p$
and get that
$q=p\cup \pi p$
and get that
But since
![]() $\dot e$
and
$\dot e$
and
![]() $\pi \dot e$
are compatible, it must be that
$\pi \dot e$
are compatible, it must be that
![]() $q\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot x=\pi \dot x$
, and since
$q\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot x=\pi \dot x$
, and since
![]() $\pi \dot e$
is compatible with
$\pi \dot e$
is compatible with
![]() $\dot e'$
, it must be that
$\dot e'$
, it must be that
![]() $\dot e'$
, if it decides the value of
$\dot e'$
, if it decides the value of
![]() $\dot f(\check \alpha )$
at all, decides the same value.
$\dot f(\check \alpha )$
at all, decides the same value.
It follows that in M a condition whose domain includes S must have decided all the values of
![]() $\dot f$
, and therefore it is a
$\dot f$
, and therefore it is a
![]() $\mathbb Q_1$
-name for a sequence already in M.
$\mathbb Q_1$
-name for a sequence already in M.
Finally, we need to prove that the generic partition is amorphous. Suppose that this is not the case and let
![]() $\dot B$
be a
$\dot B$
be a
![]() $\mathbb Q_1$
-name in M for an infinite co-infinite set of equivalence classes, and as before denote by
$\mathbb Q_1$
-name in M for an infinite co-infinite set of equivalence classes, and as before denote by
![]() $[\dot B]$
a
$[\dot B]$
a
![]() ${\mathbb P}$
-name in
${\mathbb P}$
-name in
![]() $\mathsf {HS}$
for
$\mathsf {HS}$
for
![]() $\dot B$
. Let
$\dot B$
. Let
![]() $S\in [\kappa ]^{<\kappa }$
such that
$S\in [\kappa ]^{<\kappa }$
such that
![]() $\operatorname {\mathrm {fix}}(S)\subseteq \operatorname {\mathrm {sym}}([\dot B])$
, and let p and
$\operatorname {\mathrm {fix}}(S)\subseteq \operatorname {\mathrm {sym}}([\dot B])$
, and let p and
![]() $\dot e$
be such that
$\dot e$
be such that
![]() $\operatorname {\mathrm {supp}} p=\operatorname {\mathrm {dom}} E=S$
and
$\operatorname {\mathrm {supp}} p=\operatorname {\mathrm {dom}} E=S$
and
![]() $p\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e\mathrel {\Vdash }_{\mathbb Q_1}[\dot B]$
is infinite and co-infinite.
$p\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e\mathrel {\Vdash }_{\mathbb Q_1}[\dot B]$
is infinite and co-infinite.
Pick some
![]() $\alpha ,\beta \notin S$
, and extend p and
$\alpha ,\beta \notin S$
, and extend p and
![]() $\dot e$
to
$\dot e$
to
![]() $p'$
and
$p'$
and
![]() $\dot e'$
such that:
$\dot e'$
such that:
-
(1)
 $p'\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e'\mathrel {\Vdash }_{\mathbb Q_1}\dot e'(\dot a_{\alpha })\in [\dot B]$
and
$p'\mathrel {\Vdash }^{\mathsf {HS}}_{\mathbb P}\dot e'\mathrel {\Vdash }_{\mathbb Q_1}\dot e'(\dot a_{\alpha })\in [\dot B]$
and
 $\dot e'(\dot a_{\beta })\notin [\dot B]$
.
$\dot e'(\dot a_{\beta })\notin [\dot B]$
. -
(2)
 $\alpha $
and
$\alpha $
and
 $\beta $
are added to new cells in
$\beta $
are added to new cells in
 $E'$
, as opposed to cells that already exist in E.
$E'$
, as opposed to cells that already exist in E. -
(3) The cardinality of the cells of
 $\alpha $
and
$\alpha $
and
 $\beta $
in
$\beta $
in
 $E'$
is equal.
$E'$
is equal. -
(4)
 $p'\mathbin \upharpoonright E'(\alpha )$
and
$p'\mathbin \upharpoonright E'(\alpha )$
and
 $p'\mathbin \upharpoonright E'(\beta )$
have the same type, in other words, they can be switched by some
$p'\mathbin \upharpoonright E'(\beta )$
have the same type, in other words, they can be switched by some
 $\pi \in \mathscr {G}$
.
$\pi \in \mathscr {G}$
.
This can be done by first finding extensions so that (1)–(3) are satisfied, then in
![]() $V,$
we just add more elements to the cells of
$V,$
we just add more elements to the cells of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
to ensure that we can find
$\beta $
to ensure that we can find
![]() $p'$
as in the (4).
$p'$
as in the (4).
Note that switching the two cells, of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, in
$\beta $
, in
![]() $E'$
can be done, if at all, without moving any point in S. Picking such automorphism,
$E'$
can be done, if at all, without moving any point in S. Picking such automorphism,
![]() $\pi $
, we get that
$\pi $
, we get that
![]() $\pi p'=p'$
and
$\pi p'=p'$
and
![]() $\pi \dot e'=\dot e'$
, and by
$\pi \dot e'=\dot e'$
, and by
![]() $\pi \in \operatorname {\mathrm {fix}}(S)$
we also get that
$\pi \in \operatorname {\mathrm {fix}}(S)$
we also get that
![]() $\pi [\dot B]=[\dot B]$
. This is an outright contradiction, since applied to (1) the roles of
$\pi [\dot B]=[\dot B]$
. This is an outright contradiction, since applied to (1) the roles of
![]() $\dot a_{\alpha }$
and
$\dot a_{\alpha }$
and
![]() $\dot a_{\beta }$
are switched.
$\dot a_{\beta }$
are switched.
We point out that the proof that
![]() $\mathbb Q_2$
adds an amorphous set is based on the proof of Theorem 4.5 in [Reference Monro11], where Monro uses a similar argument over the Cohen model, i.e., the case where
$\mathbb Q_2$
adds an amorphous set is based on the proof of Theorem 4.5 in [Reference Monro11], where Monro uses a similar argument over the Cohen model, i.e., the case where
![]() $\kappa =\omega $
, to add an amorphous set.
$\kappa =\omega $
, to add an amorphous set.
Corollary 5.3
![]() $\mathsf {ZF}+\mathsf {DC}_{<\kappa }$
cannot prove that a
$\mathsf {ZF}+\mathsf {DC}_{<\kappa }$
cannot prove that a
![]() $\sigma $
-sequential forcing is
$\sigma $
-sequential forcing is
![]() $\sigma $
-distributive for any uncountable
$\sigma $
-distributive for any uncountable
![]() $\kappa $
.
$\kappa $
.
6 Open problems
We saw that
![]() $\mathsf {ZF}$
cannot prove that a
$\mathsf {ZF}$
cannot prove that a
![]() $\sigma $
-sequential forcing is
$\sigma $
-sequential forcing is
![]() $\sigma $
-distributive; but we also saw that assuming the consistency of suitable large cardinal axioms, the equivalence of
$\sigma $
-distributive; but we also saw that assuming the consistency of suitable large cardinal axioms, the equivalence of
![]() $\sigma $
-sequential to
$\sigma $
-sequential to
![]() $\sigma $
-distributive does not imply the Axiom of Choice either. Indeed, we can replace that
$\sigma $
-distributive does not imply the Axiom of Choice either. Indeed, we can replace that
![]() $\sigma $
by any
$\sigma $
by any
![]() ${\leq }|X|$
.
${\leq }|X|$
.
Question 6.1 What is the consistency strength of
![]() $\mathsf {ZF}+\lnot \mathsf {AC}+$
“
$\mathsf {ZF}+\lnot \mathsf {AC}+$
“
![]() $\sigma $
-sequential forcing is
$\sigma $
-sequential forcing is
![]() $\sigma $
-distributive”? Is it any different to
$\sigma $
-distributive”? Is it any different to
![]() $\forall X({\leq }|X|\text {-sequential}\to {\leq }|X|\text {-distributive})$
?
$\forall X({\leq }|X|\text {-sequential}\to {\leq }|X|\text {-distributive})$
?
In [Reference Karagila and Schlicht10] the first author proved with Philipp Schlicht that if A is an infinite set such that
![]() $[A]^{<\omega }$
is Dedekind-finite,Footnote
16
then the forcing
$[A]^{<\omega }$
is Dedekind-finite,Footnote
16
then the forcing
![]() $\operatorname {\mathrm {Add}}(A,1)$
given by finite partial functions
$\operatorname {\mathrm {Add}}(A,1)$
given by finite partial functions
![]() $p\colon A\to 2$
, which is clearly not
$p\colon A\to 2$
, which is clearly not
![]() $\sigma $
-distributive,Footnote
17
satisfies that every antichain is finite, and equivalently “every forcing statement is decided by a finite set.”Footnote
18
These are conditions (2) and (4) in Theorem 6.1 in the paper.
$\sigma $
-distributive,Footnote
17
satisfies that every antichain is finite, and equivalently “every forcing statement is decided by a finite set.”Footnote
18
These are conditions (2) and (4) in Theorem 6.1 in the paper.
Claim 6.2 Suppose that A is an infinite set such that
![]() $[A]^{<\omega }$
is Dedekind-finite, then
$[A]^{<\omega }$
is Dedekind-finite, then
![]() $\operatorname {\mathrm {Add}}(A,1)$
is
$\operatorname {\mathrm {Add}}(A,1)$
is
![]() $\sigma $
-sequential.
$\sigma $
-sequential.
Proof Let
![]() $\dot f$
be a name such that
$\dot f$
be a name such that
![]() for some
for some
![]() $\alpha $
.
$\alpha $
.
Consider for each
![]() $x\in V_{\alpha }$
the sets
$x\in V_{\alpha }$
the sets
![]() $M_n^x$
of maximal conditions
$M_n^x$
of maximal conditions
![]() $p\in \operatorname {\mathrm {Add}}(A,1)$
which force
$p\in \operatorname {\mathrm {Add}}(A,1)$
which force
![]() $\dot f\mathbin \upharpoonright \check n=\check x$
. This set is finite, so the set
$\dot f\mathbin \upharpoonright \check n=\check x$
. This set is finite, so the set
![]() $X=\bigcup \{\operatorname {\mathrm {dom}} p\mid p\in M_n^x\}$
is a finite set. For each x, consider now the finite antichain
$X=\bigcup \{\operatorname {\mathrm {dom}} p\mid p\in M_n^x\}$
is a finite set. For each x, consider now the finite antichain
![]() $A_x$
,
$A_x$
,
For any possible
![]() $x,$
where
$x,$
where
![]() $M_n^x$
is not empty to begin with,
$M_n^x$
is not empty to begin with,
![]() $A_x$
is a uniformly defined antichain, and moreover, if
$A_x$
is a uniformly defined antichain, and moreover, if
![]() $x\neq y$
, then
$x\neq y$
, then
![]() $A_x\cup A_y$
is an antichain. Therefore,
$A_x\cup A_y$
is an antichain. Therefore,
![]() $F_n$
, defined as
$F_n$
, defined as
![]() $\bigcup \{A_x\mid M_n^x\neq \varnothing \}$
, is an antichain as well, and therefore finite.
$\bigcup \{A_x\mid M_n^x\neq \varnothing \}$
, is an antichain as well, and therefore finite.
Finally, consider now the sequence of finite sets given by
![]() $\bigcup \{\operatorname {\mathrm {dom}} p\mid p\in F_n\}$
. Note that this sequence is increasing, since a condition in
$\bigcup \{\operatorname {\mathrm {dom}} p\mid p\in F_n\}$
. Note that this sequence is increasing, since a condition in
![]() $F_{n+1}$
must extend some condition in
$F_{n+1}$
must extend some condition in
![]() $F_n$
. It follows that the sequence is eventually constant, with some value
$F_n$
. It follows that the sequence is eventually constant, with some value
![]() $A'$
and therefore if
$A'$
and therefore if
![]() $A'\subseteq \operatorname {\mathrm {dom}} p$
, then p must decide
$A'\subseteq \operatorname {\mathrm {dom}} p$
, then p must decide
![]() $\dot f\mathbin \upharpoonright \check n$
for all
$\dot f\mathbin \upharpoonright \check n$
for all
![]() $n<\omega $
, which is to say that p forces that
$n<\omega $
, which is to say that p forces that
![]() $\dot f$
is in the ground model.
$\dot f$
is in the ground model.
Easily the proof above extends to any
![]() $\kappa $
, so
$\kappa $
, so
![]() $\mathrm {COrd}\subseteq \mathcal S_{\operatorname {\mathrm {Add}}(A,1)}$
, the sequentiality spectrum of
$\mathrm {COrd}\subseteq \mathcal S_{\operatorname {\mathrm {Add}}(A,1)}$
, the sequentiality spectrum of
![]() $\operatorname {\mathrm {Add}}(A,1)$
. This extends Theorem 6.1 in [Reference Karagila and Schlicht10], in which a list of properties of
$\operatorname {\mathrm {Add}}(A,1)$
. This extends Theorem 6.1 in [Reference Karagila and Schlicht10], in which a list of properties of
![]() $\operatorname {\mathrm {Add}}(A,1)$
which are all equivalent to
$\operatorname {\mathrm {Add}}(A,1)$
which are all equivalent to
![]() $[A]^{<\omega }$
being Dedekind-finite are given. Specifically, conditions (8) and (9) which state that no reals and no sets of ordinals are added.
$[A]^{<\omega }$
being Dedekind-finite are given. Specifically, conditions (8) and (9) which state that no reals and no sets of ordinals are added.
Question 6.3 Suppose that every
![]() $\sigma $
-sequential forcing is
$\sigma $
-sequential forcing is
![]() $\sigma $
-distributive. The above claim show that
$\sigma $
-distributive. The above claim show that
![]() $[A]^{<\omega }$
is Dedekind-infinite for any infinite set. Can we say more?
$[A]^{<\omega }$
is Dedekind-infinite for any infinite set. Can we say more?
We finish this paper with two slightly orthogonal questions about the Foreman Maximality Principle (see [Reference Foreman, Magidor and Shelah3]), which states that every nontrivial forcing adds a real or collapses cardinals. The consistency of this principle with
![]() $\mathsf {ZFC}$
is still open, but it is known to imply the consistency of large cardinals, as it implies that
$\mathsf {ZFC}$
is still open, but it is known to imply the consistency of large cardinals, as it implies that
![]() $\mathsf {GCH}$
fails everywhere. We saw that in the Gitik model every nontrivial forcing must add a countable sequence of ground model elements. But we can show that not every forcing adds a real, e.g., by showing that some of the collapsing sequences that are removed from the model by symmetric arguments are generic over it, and adding them back will not add reals.
$\mathsf {GCH}$
fails everywhere. We saw that in the Gitik model every nontrivial forcing must add a countable sequence of ground model elements. But we can show that not every forcing adds a real, e.g., by showing that some of the collapsing sequences that are removed from the model by symmetric arguments are generic over it, and adding them back will not add reals.
Question 6.4 Does the Foreman Maximality Principle hold in the Gitik model?
Question 6.5 What happens when we consider “collapse cardinals” in its general sense, meaning we add a bijection between two sets that did not have a bijection between them in the ground model. Does this modified principle hold in the Gitik model? Can it hold in
![]() $\mathsf {ZF}$
without large cardinals?
$\mathsf {ZF}$
without large cardinals?
Acknowledgment
The authors would like to thank Jonathan Kirby and Mark Kamsma for their comments regarding the introduction of this paper. The authors would also like to thank the anonymous referee for their helpful remarks.