Hostname: page-component-65f69f4695-bj4tz Total loading time: 0 Render date: 2025-06-29T19:17:17.890Z Has data issue: false hasContentIssue false
  • English
  • Français

A Spectral Theorem for Hermitian Operators of Meromorphic Type on Banach Spaces

Published online by Cambridge University Press:  20 November 2018

T. Owusu-Ansah
T. Owusu-Ansah*
Affiliation:
Mathematics Department, The University of Science and Technology, Kumasi, Ghana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that if T is a compact self-adjoint operator on a Hilbert space whose distinct non-zero eigenvalues {λn} are arranged so that |λn|≥|λn+1| for n = 1, 2…. and if En in the spectral projection corresponding to λn, then 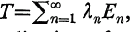with convergence in the uniform operator topology. With the generalisation of self-adjoint operators on Hilbert spaces to Hermitian operators on Banach spaces by Vidav and Lumer, Bonsall gave a partial analogue of this result for Banach spaces when he proved the following theorem.

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 17 , Issue 5 , February 1975 , pp. 703 - 708
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Berkson, E., Sequel to a paper of A. E. Taylor, Pac. J. of Math., 10 (1960), 767–776.Google Scholar
2. Bonsall, F., Hermitian operators on Banach spaces, Colloquia Mathematica Societatis Janos Bolyai, 5, Hilbert space operators, Tihany (Hungary), 1970.Google Scholar
3. Dunford, N. and Schwartz, J., Linear operators, Part I, Interscience Publishers, Inc., New York, 1966.Google Scholar
4. Hille, E., Analytic function theory, vol. I, Ginn and Co., New York, 1959.Google Scholar
5. Hille, E. and Phillips, R. S., Functional Analysis and semi-groups, Amer. Math. Soc. Coll. Publications, 31 (1957).Google Scholar
6. Lumer, G., Semi-inner product spaces, Trans. American Math. Soc, 100 (1961), 29–43.Google Scholar
7. Palmer, T., Unbounded normal operators on Banach spaces, Trans. Amer. Math. Soc. 33 (1968), 385–414.Google Scholar
8. Rudin, W., Real and complex analysis, McGraw-Hill Book Co., New York, 1966.Google Scholar
9. Taylor, A. E., Introduction to Functional Analysis, J. Wiley and Sons, Inc., New York, 1958.Google Scholar
10. Taylor, A. E., Mittag-Leffler expansions and spectral theory, Pac. J. of Math., 10 (1960), 1049–1066.Google Scholar
11. Taylor, A. E., Spectral theory and Mittag-Leffler type expansions of the resolvent, Proc. of the International Symposium on Linear spaces, The Hebrew University, Jersualem, 1960.Google Scholar
12. Taylor, A. E. and Derr, J., Operators of meromorphic type with multiple poles of the resolvent, Pac. J. of Math., 12 (1962), 85–111.Google Scholar
13. Vidav, I., Eine metrische Kennzeichnung der selbstadjungierten operatoren, Math. Zeit, 66 (1956), 121–128.Google Scholar