Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T08:07:17.429Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherical Functions on SO0(p, q)/ SO(p) × SO(q)

Published online by Cambridge University Press:  20 November 2018

P. Sawyer
P. Sawyer*
Affiliation:
Department of Mathematics and Computer Science, Laurentian University, Sudbury, Ontario, P3E 5C6, email: sawyer@cs.laurentian.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An integral formula is derived for the spherical functions on the symmetric space 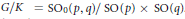${G}/{K\,=\,{\text{S}{{\text{O}}_{0}}\left( p,\,q \right)}/{\text{SO}\left( p \right)\,\times \,\text{SO}\left( q \right)}\;}\;$. This formula allows us to state some results about the analytic continuation of the spherical functions to a tubular neighbourhood of the subalgebra a of the abelian part in the decomposition 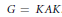$G\,=\,KAK$. The corresponding result is then obtained for the heat kernel of the symmetric space ${\text{S}{{\text{O}}_{0}}\left( p,\,q \right)}/{\text{SO}\left( p \right)\,\times \,\text{SO}\left( q \right)}\;$ using the Plancherel formula.

In the Conclusion, we discuss how this analytic continuation can be a helpful tool to study the growth of the heat kernel.

Keywords

33C5517B2053C35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 4 , 01 December 1999 , pp. 486 - 498
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Anker, Jean-Philippe, Le noyau de la chaleur sur les espaces sym´etriques U(p, q)/U(p)×U(q). Lectures Notes in Mathematics 1359, Springer-Verlag, New York, 1988, 60–82.Google Scholar
[2] Clerc, Jean-Louis, Fonctions sph´eriques des espaces sym´etriques compacts. Trans. Amer. Math. Soc. (1) 306 (1988), 421–431.Google Scholar
[3] Golse, F., Leichtnam, E. and Stenzel, M., Intrinsic microlocal analysis and inversion formulae for the heat equation on compact real-analytic Riemannian manifolds. Ann. Sci. l’E´ cole Norm. Sup. (4), 29 (1996), 669–736.Google Scholar
[4] Heckman, G. J., Root systems and hypergeometric functions II. Compositio Math. 64 (1987), 353–373.Google Scholar
[5] Heckman, G. J. and Opdam, E. M., Root systems and hypergeometric functions I. Compositio Math. 64 (1987), 329–352.Google Scholar
[6] Helgason, Sigurdur, Differential geometry, Lie groups, and symmetric spaces. Academic Press, 1978.Google Scholar
[7] Helgason, Sigurdur, Groups and geometric analysis, Academic Press, 1984.Google Scholar
[8] BhanuMurti, T. S., Plancherel's measure for the factor space SL(n, R)= SO(n, R). Soviet Math. Dokl. 1 (1960), 860–862.Google Scholar
[9] Opdam, E. M., Root systems and hypergeometric functions III. Compositio Math. 67 (1988), 41–49.Google Scholar
[10] Opdam, E. M., Root systems and hypergeometric functions IV. Compositio Math. 67 (1988), 191–209.Google Scholar
[11] Opdam, E. M.. An analogue of the Gauss summation formula for hypergeometric functions related to root systems. Math. Z. 212 (1993), 313–336.Google Scholar
[12] Opdam, E. M., Harmonic analysis for certain representations of graded Hecke algebras. Acta Math. 175 (1995), 75–121.Google Scholar
[13] Sawyer, Patrice, The heat equation on spaces of positive definite matrices. Canad. J. Math. (3) 44 (1992), 624–651.Google Scholar
[14] Sawyer, Patrice, On an upper bound for the heat kernel on SU*(2n)= Sp(n). Canad. Math. Bull. (3) 37 (1994), 408–418.Google Scholar
[15] Sawyer, Patrice, Spherical functions on symmetric cones. Trans. Amer. Math. Soc. 349 (1997), 3569–3584.Google Scholar
[16] Sawyer, Patrice, Estimates for the heat kernel on SL(n, R)= SO(n). Canad. J. Math. (2) 49 (1997), 359–372.Google Scholar
[17] Van den Ban, E. P., Asymptotic expansions and integral formulas for eigenfunctions on a semisimple Lie group. Thesis Utrecht, 1983.Google Scholar