Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-08T10:33:19.655Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherical Space Forms: Homotopy Types and Self-Equivalences for the Group (ℤ/a ⋊ ℤ/b) × SL2 (p)

Published online by Cambridge University Press:  20 November 2018

Marek Golasiński  and
Daciberg Lima Gonçalves
Marek Golasiński
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń Poland e-mail: marek@mat.uni.torun.pl
Daciberg Lima Gonçalves
Affiliation:
Department of Mathematics-IME, University of São Paulo, Caixa Postal 66.281-AG., Cidade de São Paulo, 05311-970 São Paulo, Brasil e-mail: dlgoncal@ime.usp.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 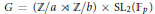$G=\left( \mathbb{Z}/a\rtimes \mathbb{Z}/b \right)\times \text{S}{{\text{L}}_{2}}\left( {{\mathbb{F}}_{p}} \right)$, and let 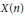$X\left( n \right)$ be an 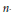$n$-dimensional 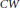$CW$-complex of the homotopy type of an 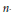$n$-sphere. We study the automorphism group 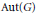$\text{Aut}\left( G \right)$ in order to compute the number of distinct homotopy types of spherical space forms with respect to free and cellular 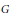$G$-actions on all 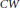$CW$-complexes 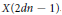$X\left( 2dn-1 \right)$, where 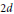$2d$ is the period of 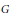$G$. The groups 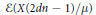$\varepsilon \left( X\left( 2dn-1 \right)/\mu \right)$ of self homotopy equivalences of space forms 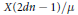$X\left( 2dn-1 \right)/\mu$ associated with free and cellular 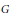$G$-actions 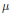$\mu$ on 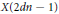$X\left( 2dn-1 \right)$ are determined as well.

Keywords

55M3555P1520E2220F2857S17automorphism groupCW-complexfree and cellular G-actiongroup of self homotopy equivalencesLyndon-Hochschild-Serre spectral sequencespecial (linear) groupspherical space form
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 2 , 01 June 2007 , pp. 206 - 214
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Adem, A. and Milgam, R. J., Cohomology of Finite Groups. Grundlehren der Mathematischen Wissenschaften 309, Springer-Verlag, Berlin, 1994.Google Scholar
[2] Adem, A. and Davis, J. F., Topics in transformation groups. In: Handbook of Geometic Topology, North-Holland, Amsterdam, 2002, pp. 1–54.Google Scholar
[3] Cartan, H. and Eilenberg, S., Homological Algebra. Princeton University Press, Princeton, NJ, 1956.Google Scholar
[4] Fiedorowicz, Z. and Priddy, S., Homology of Classical Groups over Finite Fields and their Associated Infinite Loop Spaces. Lecture Notes in Mathematics 674, Springer, Berlin, 1978.Google Scholar
[5] Golasiński, M. and Gonçalves, D. L., Homotopy spherical space forms—a numerical bound for homotopy types. Hiroshima Math. J. 31(2001), no. 1, 107–116.Google Scholar
[6] Golasiński, M. and Gonçalves, D. L., Spherical space forms—homotopy types and self-equivalences. In: Categorical Decomposition Techniques in Algebraic Topology, Progr. Math. 215, Birkhäuser, Basel, 2004, pp. 153–165.Google Scholar
[7] Golasiński, M. and Gonçalves, D. L., Spherical space forms—homotopy types and self-equivalences for the groups . Topology Appl. 146/147(2005), 451–470.Google Scholar
[8] Golasiński, M. and Gonçalves, D. L., Spherical space forms—homotopy types and self-equivalences for the groups . Journal of Homotopy and Related Structures 1(2006), no. 1, 29–45.Google Scholar
[9] Hua, L. K., On the automorphisms of the sympletic group over any field. Ann. of Math. 49(1948), 739–759.Google Scholar
[10] Madsen, I., Thomas, C. B., and Wall, C. T. C., The topological spherical space form problem. II. Existence of free actions. Topology 15(1976), no. 4, 375–382.Google Scholar
[11] O’Meara, O. T., Lectures on linear groups. American Mathematical Society, Providence, RI, 1974.Google Scholar
[12] Rutter, J. W., Spaces of Homotopy Self-Equivalences. A Survey. Lecture Notes in Mathematics 1662, Springer-Verlag, Berlin, 1997.Google Scholar
[13] Smallen, D., The group of self-equivalences of certain complexes. Pacific J. Math. 54(1974), 269–276.Google Scholar
[14] Schreier, O. and van der Waerden, B. L., Die Automorphismen der projektiven Gruppen. Hamburg Univ. Math. Seminar, Abh. 6, 1928, 303–322.Google Scholar
[15] Swan, R. G., The p-period of a finite group. Illinois J. Math. 4(1960), 341–346.Google Scholar
[16] Swan, R. G., Periodic resolutions for finite groups. Ann. of Math. 72(1960), no. 2, 267–291.Google Scholar
[17] Thomas, C. B. and Wall, C. T. C., The topological spherical space form problem. I. Compositio Math. 23(1971), 101–114.Google Scholar
[18] Thomas, C. B. and Wall, C. T. C., Characteristic classes and the cohomology of finite groups. Cambridge Studies in Advanced Mathematics 9, Cambridge University Press, Cambridge, 1986.Google Scholar