Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-12T05:19:52.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Squared Chromatic Number Without Claws or Large Cliques

Part of: Graph theory

Published online by Cambridge University Press:  09 January 2019

Wouter Cames van Batenburg  and
Ross J. Kang
Wouter Cames van Batenburg
Affiliation:
Computer Science Department, Faculté des Sciences, Université Libre de Bruxelles, Campus de la Plaine, CP212, B-1050 Brussels, Belgium Email: wcamesva@ulb.ac.be
Ross J. Kang
Affiliation:
Department of Mathematics, Radboud University Nijmegen, Postbus 9010, 6500 GL Nijmegen, The Netherlands Email: ross.kang@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 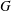$G$ be a claw-free graph on $n$ vertices with clique number 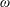$\unicode[STIX]{x1D714}$, and consider the chromatic number 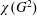$\unicode[STIX]{x1D712}(G^{2})$ of the square 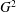$G^{2}$ of 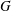$G$. Writing 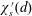$\unicode[STIX]{x1D712}_{s}^{\prime }(d)$ for the supremum of 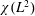$\unicode[STIX]{x1D712}(L^{2})$ over the line graphs 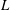$L$ of simple graphs of maximum degree at most 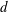$d$, we prove that 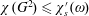$\unicode[STIX]{x1D712}(G^{2})\leqslant \unicode[STIX]{x1D712}_{s}^{\prime }(\unicode[STIX]{x1D714})$ for 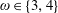$\unicode[STIX]{x1D714}\in \{3,4\}$. For 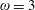$\unicode[STIX]{x1D714}=3$, this implies the sharp bound 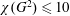$\unicode[STIX]{x1D712}(G^{2})\leqslant 10$. For 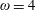$\unicode[STIX]{x1D714}=4$, this implies 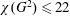$\unicode[STIX]{x1D712}(G^{2})\leqslant 22$, which is within 2 of the conjectured best bound. This work is motivated by a strengthened form of a conjecture of Erdős and Nešetřil.

Keywords

graph colouringErdős–Nešetřil conjectureclaw-free graph

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C35: Extremal problems 05C70: Factorization, matching, partitioning, covering and packing
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 1 , March 2019 , pp. 23 - 35
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author W. C. v. B. was supported by NWO grant 613.001.217. Author R. J. K. is supported by a NWO Vidi Grant, reference 639.032.614.

References

Andersen, L. D., The strong chromatic index of a cubic graph is at most 10. Topological, algebraical and combinatorial structures . Discrete Math. 108(1992), no. 1–3, 231–252., 1992. https://doi.org/10.1016/0012-365X(92)90678-9.Google Scholar
Chudnovsky, M. and Seymour, P., The structure of claw-free graphs . In: Surveys in combinatorics 2005, London Math. Soc. Lecture Note Ser., 327, Cambridge University Press, Cambridge, 2005, pp. 153–171. https://doi.org/10.1017/CBO9780511734885.008.Google Scholar
Chudnovsky, M. and Seymour, P., Claw-free graphs VI. Colouring . J. Combin. Theory Ser. B 100(2010), 560–572. https://doi.org/10.1016/j.jctb.2010.04.005.Google Scholar
Cranston, D. W., Strong edge-coloring of graphs with maximum degree 4 using 22 colors . Discrete Math. 306(2006), 2772–2778. https://doi.org/10.1016/j.disc.2006.03.053.Google Scholar
de Joannis de Verclos, R., Kang, R. J., and Pastor, L., Colouring squares of claw-free graphs . Canad. J. Math., to appear. https://doi.org/10.4153/CJM-2017-029-9.Google Scholar
Erdős, P., Problems and results in combinatorial analysis and graph theory . In: Proceedings of the First Japan Conference on Graph Theory and Applications (Hakone, 1986), Discrete Math. 72(1988), 81–92. https://doi.org/10.1016/0012-365X(88)90196-3.Google Scholar
Erdős, P. and Szekeres, G., A combinatorial problem in geometry . Compositio Math. 2(1935), 463–470.Google Scholar
Horák, P., He, Q., and Trotter, W. T., Induced matchings in cubic graphs . J. Graph Theory 17(1993), 151–160. https://doi.org/10.1002/jgt.3190170204.Google Scholar
Molloy, M. and Reed, B., A bound on the strong chromatic index of a graph . J. Combin. Theory Ser. B 69(1997), 103–109. https://doi.org/10.1006/jctb.1997.1724.Google Scholar