Hostname: page-component-54dcc4c588-b5cpw Total loading time: 0 Render date: 2025-09-24T23:19:02.779Z Has data issue: false hasContentIssue false
  • English
  • Français

The Wedge-of-the-edge Theorem: Edge-of-the-wedge Type Phenomenon Within the Common Real Boundary

Part of: Holomorphic functions of several complex variables

Published online by Cambridge University Press:  07 January 2019

J. E. Pascoe
J. E. Pascoe*
Affiliation:
Department of Mathematics, University of Florida, Gainesville, FL 32611, USA Email: pascoej@ufl.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The edge-of-the-wedge theorem in several complex variables gives the analytic continuation of functions defined on the poly upper half plane and the poly lower half plane, the set of points in 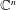$\mathbb{C}^{n}$ with all coordinates in the upper and lower half planes respectively, through a set in real space, $\mathbb{R}^{n}$. The geometry of the set in the real space can force the function to analytically continue within the boundary itself, which is qualified in our wedge-of-the-edge theorem. For example, if a function extends to the union of two cubes in 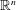$\mathbb{R}^{n}$ that are positively oriented with some small overlap, the functions must analytically continue to a neighborhood of that overlap of a fixed size not depending of the size of the overlap.

Keywords

edge-of-the-wedge theoremseveral complex variablesanalytic continuation

MSC classification

Primary: 32A40: Boundary behavior of holomorphic functions

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 417 - 427
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Partially supported by National Science Foundation Mathematical Science Postdoctoral Research Fellowship DMS 1606260.

References

Agler, J. and McCarthy, J. E., Distinguished varieties . Acta Math. 194(2005), 133–153. https://doi.org/10.1007/BF02393219.Google Scholar
Agler, J. and McCarthy, J. E., Hyperbolic algebraic and analytic curves . Indiana Univ. Math. J. 56(2997), 2899–2933. https://doi.org/10.1512/iumj.2007.56.3263.Google Scholar
Agler, J., McCarthy, J. E., and Stankus, M., Toral algebraic sets and function theory on polydisks . J. Geom. Anal. 16(2006), 551–562. https://doi.org/10.1007/BF02922130.Google Scholar
Agler, J., McCarthy, J. E., and Young, N. J., Operator monotone functions and Löwner functions of several variables . Ann. of Math. 176(2012), 1783–1826. https://doi.org/10.4007/annals.2012.176.3.7.Google Scholar
Bickel, K., Pascoe, J. E., and Sola, A., Derivatives of rational inner functions: geometry of singularities and integrability at the boundary . Proc. Lond. Math. Soc., to appear. https://doi.org/10.1112/plms.12072.Google Scholar
Bogoliubov, N. N., Medvedev, B. V., and Polivanov, M. K., Problems in the Theory of Dispersion Relations. Institute for Advanced Study Press, Princeton, 1958.Google Scholar
Cohn, D. L., Measure theory. Birkhäuser, Boston, Basel, Stuttgart, 1980.Google Scholar
Epstein, H., Generalization of the “edge-of-the-wedge” theorem . J. Mathematical Phys 1(1960), 524–531. https://doi.org/10.1063/1.1703688.Google Scholar
Knese, G., Polynomials defining distinguished varieties . Trans. Amer. Math. Soc. 362(2010), 5635–5655. https://doi.org/10.1090/S0002-9947-2010-05275-4.Google Scholar
Pascoe, J. E., Note on Löwner’s theorem in several commuting variables of Agler, McCarthy and Young. submitted, 2014.Google Scholar
Pascoe, J. E., A wedge-of-the-edge theorem: analytic continuation of multivariable Pick functions in and around the boundary . Bull. Lond. Math. Soc. 49(2017), 916–925. https://doi.org/10.1112/blms.12079.Google Scholar
Rudin, W., Function theory in polydiscs. Benjamin, New York, 1969.Google Scholar
Rudin, W., Lectures on the edge-of-the-wedge theorem. Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, 6, American Mathematical Society, Providence, 1971.Google Scholar
Szegő, G., Orthogonal polynomials, American Mathematical Society Colloquium Publications, 23, Providence, RI, 1939.Google Scholar
Vladimirov, V. S., Zharinov, V. V., and Sergeev, A. G., Bogolyubov’s edge-of-the-wedge theorem, its development and applications . Russian Math. Surveys 5(1994), 51–65.Google Scholar