Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-23T09:26:36.836Z Has data issue: false hasContentIssue false
  • English
  • Français

The bunkbed conjecture holds in the 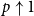$p\uparrow 1$ limit

Part of: Special processes Graph theory

Published online by Cambridge University Press:  14 December 2022

Tom Hutchcroft Open the ORCID record for Tom Hutchcroft [Opens in a new window] ,
Alexander Kent  and
Petar Nizić-Nikolac
Tom Hutchcroft*
Affiliation:
The Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA
Alexander Kent
Affiliation:
University of Warwick, Coventry, CV4 7AL, UK
Petar Nizić-Nikolac
Affiliation:
University of Cambridge, Cambridge, CB3 0WB, UK
*
*Corresponding author. Email: t.hutchcroft@caltech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 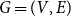$G=(V,E)$ be a countable graph. The Bunkbed graph of 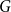$G$ is the product graph 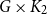$G \times K_2$ , which has vertex set 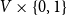$V\times \{0,1\}$ with “horizontal” edges inherited from 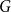$G$ and additional “vertical” edges connecting 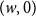$(w,0)$ and 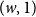$(w,1)$ for each 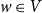$w \in V$ . Kasteleyn’s Bunkbed conjecture states that for each 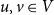$u,v \in V$ and 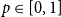$p\in [0,1]$ , the vertex 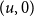$(u,0)$ is at least as likely to be connected to 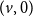$(v,0)$ as to 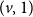$(v,1)$ under Bernoulli- 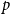$p$ bond percolation on the bunkbed graph. We prove that the conjecture holds in the 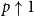$p \uparrow 1$ limit in the sense that for each finite graph 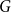$G$ there exists 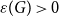$\varepsilon (G)\gt 0$ such that the bunkbed conjecture holds for 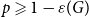$p \geqslant 1-\varepsilon (G)$ .

Keywords

percolationbunkbedconnectivityprobabilitygraph theory

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 05C99: None of the above, but in this section
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 3 , May 2023 , pp. 363 - 369
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van den Berg, J., Häggström, O. and Kahn, J. (2006) Some conditional correlation inequalities for percolation and related processes. Random Struct. Algorithms 29(4) 417–435.CrossRefGoogle Scholar
van den Berg, J. and Kahn, J. (2001) A correlation inequality for connection events in percolation. Ann. Probab. 29(1) 123–126.Google Scholar
de Buyer, P. (2016) A proof of the bunkbed conjecture on the complete graph for p = 1/2. arXiv preprint arXiv:1604.08439.Google Scholar
de Buyer, P. (2018) A proof of the bunkbed conjecture on the complete graph for p ≥ 1/2. arXiv preprint arXiv:1802.04694.Google Scholar
Grimmett, G. (1999) Percolation, Vol. 321 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], second edition, Springer.CrossRefGoogle Scholar
Grimmett, G. (2018) Probability on Graphs: Random Processes on Graphs and Lattices, Vol. 8 of Institute of Mathematical Statistics Textbooks, second edition, Cambridge University Press.CrossRefGoogle Scholar
Häggström, O. (1998) On a conjecture of Bollobás and Brightwell concerning random walks on product graphs. Combin. Probab. Comput. 7(4) 397–401.CrossRefGoogle Scholar
Häggström, O. (2003) Probability on bunkbed graphs. In Proceedings of FPSAC , Vol. 3.Google Scholar
Hara, T. and Slade, G. (1990) Mean-field critical behaviour for percolation in high dimensions. Commun. Math. Phys. 128(2) 333–391.CrossRefGoogle Scholar
Hara, T., van der Hofstad, R. and Slade, G. (2003) Critical two-point functions and the lace expansion for spread-out high-dimensional percolation and related models. Ann. Probab. 31(1) 349–408.CrossRefGoogle Scholar
van Hintum, P. and Lammers, P. (2019) The bunkbed conjecture on the complete graph. Eur. J. Combin. 76(1) 175–177.CrossRefGoogle Scholar
Leander, M. (2009) On the Bunkbed Conjecture, Självständiga Arbeten I Matematik (Independent Works in Mathematics), Matematiska Institutionen, Stockholms Universitet.Google Scholar
Linusson, S. (2011) On percolation and the bunkbed conjecture. Combin. Probab. Comput. 20(1) 103–117.CrossRefGoogle Scholar
Linusson, S. (2019) Erratum to ‘On percolation and the bunkbed conjecture. Combin. Probab. Comput. 28(6) 917–918.CrossRefGoogle Scholar
Messager, A. and Miracle-Sole, S. (1977) Correlation functions and boundary conditions in the Ising ferromagnet. J. Stat. Phys. 17(4) 245–262.CrossRefGoogle Scholar
Rudzinski, J. and Smyth, C. (2016) Equivalent formulations of the bunk bed conjecture. N. C. J. Math. Stat. 2 23–28.Google Scholar