Hostname: page-component-76dd75c94c-28gj6 Total loading time: 0 Render date: 2024-04-30T09:01:41.717Z Has data issue: false hasContentIssue false
  • English
  • Français

Economical Elimination of Cycles in the Torus

Published online by Cambridge University Press:  01 September 2009

NOGA ALON
NOGA ALON*
Affiliation:
Sackler School of Mathematics and Blavatnik School of Computer Science, Tel Aviv University, Tel Aviv, 69978, Israel and IAS, Princeton, NJ 08540, USA (e-mail: nogaa@tau.ac.il)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let m > 2 be an integer, let C2m denote the cycle of length 2m on the set of vertices [−m, m) = {−m, −m + 1, . . ., m − 2, m − 1}, and let G = G(m, d) denote the graph on the set of vertices [−m, m)d, in which two vertices are adjacent if and only if they are adjacent in C2m in one coordinate, and equal in all others. This graph can be viewed as the graph of the d-dimensional torus. We prove that one can delete a fraction of at most 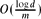of the vertices of G so that no topologically non-trivial cycles remain. This is tight up to the logd factor and improves earlier estimates by various researchers.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 5: New Directions in Algorithms, Combinatorics and Optimization , September 2009 , pp. 619 - 627
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. (1986) Eigenvalues and expanders. Combinatorica 6 83–96.CrossRefGoogle Scholar
[2]Alon, N. and Klartag, B. Economical toric spines via Cheeger's inequality. To appear.Google Scholar
[3]Bobkov, S., Houdré, C. and Tetali, P. (2000) λ∞, vertex isoperimetry and concentration. Combinatorica 20 153–172.CrossRefGoogle Scholar
[4]Bollobás, B., Kindler, G., Leader, I. and O'Donnell, R. (2006) Eliminating cycles in the discrete torus. In LATIN 2006: Theoretical Informatics, Vol. 3887 of Lecture Notes in Computer Science, Springer, Berlin, pp. 202–210. Also: Algorithmica 50 (2008) 446–454.Google Scholar
[5]Kindler, G., O'Donnell, R., Rao, A. and Wigderson, A. (2008) Rounding schemes and cubical tilings with sphere-like surface area. In Proc. FOCS 2008, pp. 189–198.Google Scholar
[6]Raz, R. (2008) A counterexample to strong parallel repetition. In Proc. FOCS 2008, pp. 369–373.CrossRefGoogle Scholar