Article contents
Most Probably Intersecting Families of Subsets
Published online by Cambridge University Press: 02 February 2012
Abstract
Let 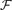 be a family of subsets of an n-element set. It is called intersecting if every pair of its members has a non-disjoint intersection. It is well known that an intersecting family satisfies the inequality |
be a family of subsets of an n-element set. It is called intersecting if every pair of its members has a non-disjoint intersection. It is well known that an intersecting family satisfies the inequality |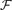 | ≤ 2n−1. Suppose that |
| ≤ 2n−1. Suppose that |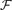 |=2n−1 + i. Choose the members of
|=2n−1 + i. Choose the members of 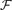 independently with probability p (delete them with probability 1 − p). The new family is intersecting with a certain probability. We try to maximize this probability by choosing
independently with probability p (delete them with probability 1 − p). The new family is intersecting with a certain probability. We try to maximize this probability by choosing 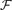 appropriately. The exact maximum is determined in this paper for some small i. The analogous problem is considered for families consisting of k-element subsets, but the exact solution is obtained only when the size of the family exceeds the maximum size of the intersecting family only by one. A family is said to be inclusion-free if no member is a proper subset of another one. It is well known that the largest inclusion-free family is the one consisting of all
appropriately. The exact maximum is determined in this paper for some small i. The analogous problem is considered for families consisting of k-element subsets, but the exact solution is obtained only when the size of the family exceeds the maximum size of the intersecting family only by one. A family is said to be inclusion-free if no member is a proper subset of another one. It is well known that the largest inclusion-free family is the one consisting of all 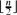 -element subsets. We determine the most probably inclusion-free family too, when the number of members is
-element subsets. We determine the most probably inclusion-free family too, when the number of members is 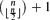 .
.
Information
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 21 , Issue 1-2: Honouring the Memory of Richard H. Schelp , March 2012 , pp. 219 - 227
- Copyright
- Copyright © Cambridge University Press 2012
References
- 7
- Cited by

