Suppose that X 1, X 2, . . . are independent identically distributed Bernoulli random variables with mean p. A Bernoulli factory for a function f takes as input X 1, X 2, . . . and outputs a random variable that is Bernoulli with mean f(p). A fast algorithm is a function that only depends on the values of X 1, . . ., XT , where T is a stopping time with small mean. When f(p) is a real analytic function the problem reduces to being able to draw from linear functions Cp for a constant C > 1. Also it is necessary that Cp ⩽ 1 − ε for known ε > 0. Previous methods for this problem required extensive modification of the algorithm for every value of C and ε. These methods did not have explicit bounds on 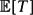$\mathbb{E}[T]$ as a function of C and ε. This paper presents the first Bernoulli factory for f(p) = Cp with bounds on 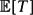$\mathbb{E}[T]$ as a function of the input parameters. In fact, supp∈[0,(1−ε)/C] 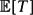$\mathbb{E}[T]$ ≤ 9.5ε−1 C. In addition, this method is very simple to implement. Furthermore, a lower bound on the average running time of any Cp Bernoulli factory is shown. For ε ⩽ 1/2, supp∈[0,(1−ε)/C] 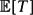$\mathbb{E}[T]$ ≥0.004Cε−1, so the new method is optimal up to a constant in the running time.