Article contents
On bucket increasing trees, clustered increasing trees and increasing diamonds
Published online by Cambridge University Press: 13 October 2021
Abstract
In this work we analyse bucket increasing tree families. We introduce two simple stochastic growth processes, generating random bucket increasing trees of size n, complementing the earlier result of Mahmoud and Smythe (1995, Theoret. Comput. Sci. 144 221–249.) for bucket recursive trees. On the combinatorial side, we define multilabelled generalisations of the tree families d-ary increasing trees and generalised plane-oriented recursive trees. Additionally, we introduce a clustering process for ordinary increasing trees and relate it to bucket increasing trees. We discuss in detail the bucket size two and present a bijection between such bucket increasing tree families and certain families of graphs called increasing diamonds, providing an explanation for phenomena observed by Bodini et al. (2016, Lect. Notes Comput. Sci. 9644 207–219.). Concerning structural properties of bucket increasing trees, we analyse the tree parameter 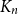 $K_n$. It counts the initial bucket size of the node containing label n in a tree of size n and is closely related to the distribution of node types. Additionally, we analyse the parameters descendants of label j and degree of the bucket containing label j, providing distributional decompositions, complementing and extending earlier results (Kuba and Panholzer (2010), Theoret. Comput. Sci. 411(34–36) 3255–3273.).
$K_n$. It counts the initial bucket size of the node containing label n in a tree of size n and is closely related to the distribution of node types. Additionally, we analyse the parameters descendants of label j and degree of the bucket containing label j, providing distributional decompositions, complementing and extending earlier results (Kuba and Panholzer (2010), Theoret. Comput. Sci. 411(34–36) 3255–3273.).
Keywords
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 1
- Cited by

