No CrossRef data available.
Article contents
On subgraphs of C2k-free graphs and a problem of Kühn and Osthus
Published online by Cambridge University Press: 04 February 2020
Abstract
Let c denote the largest constant such that every C6-free graph G contains a bipartite and C4-free subgraph having a fraction c of edges of G. Győri, Kensell and Tompkins showed that 3/8 ⩽ c ⩽ 2/5. We prove that c = 38. More generally, we show that for any ε > 0, and any integer k ⩾ 2, there is a C2k-free graph 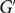 $G'$ which does not contain a bipartite subgraph of girth greater than 2k with more than a fraction
$G'$ which does not contain a bipartite subgraph of girth greater than 2k with more than a fraction 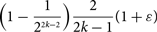 $$\Bigl(1-\frac{1}{2^{2k-2}}\Bigr)\frac{2}{2k-1}(1+\varepsilon)$$
$$\Bigl(1-\frac{1}{2^{2k-2}}\Bigr)\frac{2}{2k-1}(1+\varepsilon)$$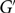 $G'$. There also exists a C2k-free graph
$G'$. There also exists a C2k-free graph 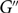 $G''$ which does not contain a bipartite and C4-free subgraph with more than a fraction
$G''$ which does not contain a bipartite and C4-free subgraph with more than a fraction 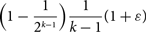 $$\Bigl(1-\frac{1}{2^{k-1}}\Bigr)\frac{1}{k-1}(1+\varepsilon)$$
$$\Bigl(1-\frac{1}{2^{k-1}}\Bigr)\frac{1}{k-1}(1+\varepsilon)$$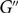 $G''$.
$G''$.
One of our proofs uses the following statement, which we prove using probabilistic ideas, generalizing a theorem of Erdős. For any ε > 0, and any integers a, b, k ⩾ 2, there exists an a-uniform hypergraph H of girth greater than k which does not contain any b-colourable subhypergraph with more than a fraction 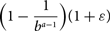 $$\Bigl(1-\frac{1}{b^{a-1}}\Bigr)(1+\varepsilon)$$
$$\Bigl(1-\frac{1}{b^{a-1}}\Bigr)(1+\varepsilon)$$
In addition, we give a new and very short proof of a result of Kühn and Osthus, which states that every bipartite C2k-free graph G contains a C4-free subgraph with at least a fraction 1/(k−1) of the edges of G. We also answer a question of Kühn and Osthus about C2k-free graphs obtained by pasting together C2l’s (with k >l ⩾ 3).
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2020

