Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-30T06:41:53.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Probably Intersecting Families are Not Nested

Published online by Cambridge University Press:  09 October 2012

PAUL A. RUSSELL  and
MARK WALTERS
PAUL A. RUSSELL
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: P.A.Russell@dpmms.cam.ac.uk)
MARK WALTERS
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, London E1 4NS, UK (e-mail: m.walters@qmul.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that an intersecting family of subsets of an n-element set can contain at most 2n−1 sets. It is natural to wonder how ‘close’ to intersecting a family of size greater than 2n−1 can be. Katona, Katona and Katona introduced the idea of a ‘most probably intersecting family’. Suppose that 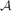is a family and that 0 < p < 1. Let 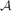(p) be the (random) family formed by selecting each set in 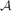independently with probability p. A family 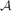is most probably intersecting if it maximizes the probability that 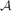(p) is intersecting over all families of size ||.

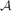Katona, Katona and Katona conjectured that there is a nested sequence consisting of most probably intersecting families of every possible size. We show that this conjecture is false for every value of p provided that n is sufficiently large.

Keywords

Primary 05D05

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 1 , January 2013 , pp. 146 - 160
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Ahlswede, R. (1980) Simple hypergraphs with maximal number of adjacent pairs of edges. J. Combin. Theory Ser. B 28 164–167.CrossRefGoogle Scholar
[2]Ahlswede, R. and Katona, G. O. H. (1978) Graphs with maximal number of adjacent pairs of edges. Acta Math. Acad. Sci. Hungar. 32 97–120.Google Scholar
[3]Frankl, P. (1977) On the minimum number of disjoint pairs in a family of finite sets. J. Combin. Theory Ser. A 22 249–251.Google Scholar
[4]Katona, G. O. H., Katona, G. Y. and Katona, Z. (2012) Most probably intersecting families of subsets. Combin. Probab. Comput. 21 219–227.Google Scholar
[5]Russell, P. A. (2012) Compressions and probably intersecting families. Combin. Probab. Comput. 21 301–313.Google Scholar
[6]Wagner, S. and Wang, H. (2009) On a problem of Ahlswede and Katona. Studia Sci. Math. Hungar. 46 423–435.Google Scholar