Hostname: page-component-cb9f654ff-rkzlw Total loading time: 0 Render date: 2025-08-03T00:41:58.523Z Has data issue: false hasContentIssue false
  • English
  • Français

Subgraph densities in a surface

Part of: Graph theory

Published online by Cambridge University Press:  11 January 2022

Tony Huynh ,
Gwenaël Joret  and
David R. Wood
Tony Huynh
Affiliation:
School of Mathematics, Monash University, Melbourne, Australia
Gwenaël Joret
Affiliation:
Département d’Informatique, Université libre de Bruxelles, Brussels, Belgium
David R. Wood*
Affiliation:
School of Mathematics, Monash University, Melbourne, Australia
*
*Corresponding author. Email: david.wood@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a fixed graph H that embeds in a surface 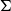$\Sigma$, what is the maximum number of copies of H in an n-vertex graph G that embeds in 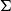$\Sigma$? We show that the answer is 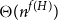$\Theta(n^{f(H)})$, where f(H) is a graph invariant called the ‘flap-number’ of H, which is independent of 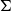$\Sigma$. This simultaneously answers two open problems posed by Eppstein ((1993) J. Graph Theory 17(3) 409–416.). The same proof also answers the question for minor-closed classes. That is, if H is a 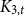$K_{3,t}$ minor-free graph, then the maximum number of copies of H in an n-vertex 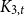$K_{3,t}$ minor-free graph G is 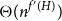$\Theta(n^{f'(H)})$, where f′(H) is a graph invariant closely related to the flap-number of H. Finally, when H is a complete graph we give more precise answers.

Keywords

graphgraph embeddingsurfacehomomorphism inequality

MSC classification

Primary: 05C10: Planar graphs; geometric and topological aspects of graph theory 05C35: Extremal problems

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 5 , September 2022 , pp. 812 - 839
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

All three authors are supported by the Australian Research Council. G. Joret is supported by an ARC grant from the Wallonia-Brussels Federation of Belgium and a CDR grant from the National Fund for Scientific Research (FNRS).

References

Alameddine, A. F. (1980) On the number of cycles of length 4 in a maximal planar graph. J. Graph Theory 4(4) 417–422.CrossRefGoogle Scholar
Alon, N. and Caro, Y. (1984) On the number of subgraphs of prescribed type of planar graphs with a given number of vertices. In Convexity and Graph Theory, Vol. 87 of North-Holland Mathematics Studies, North-Holland, pp. 25–36.Google Scholar
Alon, N., Kostochka, A. and Shikhelman, C. (2018) Many cliques in H-free subgraphs of random graphs. J. Comb. 9(4) 567–597.Google Scholar
Alon, N. and Shikhelman, C. (2016) Many T copies in H-free graphs. J. Comb. Theory Ser. B 121 146–172.CrossRefGoogle Scholar
Alon, N. and Shikhelman, C. (2019) H-free subgraphs of dense graphs maximizing the number of cliques and their blow-ups. Discrete Math. 342(4) 988–996.CrossRefGoogle Scholar
Alweiss, R., Lovett, S., Wu, K. and Zhang, J. (to appear) Improved bounds for the sunflower lemma. Ann. Math. arXiv:1908.08483.Google Scholar
Archdeacon, D. (1986) The nonorientable genus is additive. J. Graph Theory 10(3) 363–383.CrossRefGoogle Scholar
Barnette, D. W. and Edelson, A. L. (1988) All orientable 2-manifolds have finitely many minimal triangulations. Israel J. Math. 62(1) 90–98.CrossRefGoogle Scholar
Barnette, D. W. and Edelson, A. L. (1989) All 2-manifolds have finitely many minimal triangulations. Israel J. Math. 67(1) 123–128.CrossRefGoogle Scholar
Benjamini, I. and Schramm, O. (2001) Recurrence of distributional limits of finite planar graphs. Electron. J. Prob. 6(23).CrossRefGoogle Scholar
Borgs, C., Chayes, J., Kahn, J. and Lovász, L. (2013) Left and right convergence of graphs with bounded degree. Random Struct. Algorithms 42(1) 1–28.CrossRefGoogle Scholar
Bubeck, S., Edwards, K., Mania, H. and Supko, C. (2016) On paths, stars and wyes in trees. arXiv:1601.01950.Google Scholar
Bubeck, S. and Linial, N. (2016) On the local profiles of trees. J. Graph Theory 81(2) 109–119.CrossRefGoogle Scholar
Chan, T. F. N., Kráľ, D., Mohar, B. and Wood, D. R. (2021) Inducibility and universality for trees, arXiv:2102.02010.Google Scholar
Cheng, S.-W., Dey, T. K. and Poon, S.-H. (2004) Hierarchy of surface models and irreducible triangulations. Comput. Geom. 27(2) 135–150.CrossRefGoogle Scholar
Czabarka, É., Székely, L. and Wagner, S. (2017) Paths vs. stars in the local profile of trees. Electron. J. Combin. 24(P1.22).CrossRefGoogle Scholar
Dujmović, V., Fijavž, G., Joret, G., Sulanke, T. and Wood, D. R. (2011) On the maximum number of cliques in a graph embedded in a surface. Eur. J. Comb. 32(8) 1244–1252.CrossRefGoogle Scholar
Eppstein, D. (1993) Connectivity, graph minors, and subgraph multiplicity. J. Graph Theory 17(3) 409–416.CrossRefGoogle Scholar
Erdős, P. and Rado, R. (1960) Intersection theorems for systems of sets. J. London Math. Soc. Second Ser. 35(1) 85–90.CrossRefGoogle Scholar
Erdős, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Am. Math. Soc. 52 1087–1091.CrossRefGoogle Scholar
Ergemlidze, B., Methuku, A., Salia, N. and Győri, E. (2019) A note on the maximum number of triangles in a $C_5$ -free graph. J. Graph Theory 90(3) 227–230.CrossRefGoogle Scholar
Fomin, F. V., il Oum, S. and Thilikos, D. M. (2010) Rank-width and tree-width of H-minor-free graphs. Eur. J. Comb. 31(7) 1617–1628.CrossRefGoogle Scholar
Fox, J. and Wei, F. (2017) On the number of cliques in graphs with a forbidden minor. J. Comb. Theory Ser. B 126 175–197.CrossRefGoogle Scholar
Gerbner, D., Keszegh, B., Palmer, C. and Patkós, B. (2018) On the number of cycles in a graph with restricted cycle lengths. SIAM J. Discrete Math. 32(1) 266–279.CrossRefGoogle Scholar
Gerbner, D., Methuku, A. and Vizer, M. (2019) Generalized Turán problems for disjoint copies of graphs. Discrete Math. 342(11) 3130–3141.CrossRefGoogle Scholar
Gerbner, D., Nagy, Z. L. and Vizer, M. (2020) Unified approach to the generalized Turán problem and supersaturation. arXiv:2008.12093.Google Scholar
Gerbner, D. and Palmer, C. (2019) Counting copies of a fixed subgraph in F-free graphs. Eur. J. Comb. 82 103001, 15.CrossRefGoogle Scholar
Ghosh, D., Györi, E., Martin, R. R., Paulos, A., Salia, N., Xiao, C. and Zamora, O. (2021) The maximum number of paths of length four in a planar graph. Discrete Math. 344(5) 112317.CrossRefGoogle Scholar
Goodman, A. W. (1959) On sets of acquaintances and strangers at any party. Am. Math. Mon. 66 778–783.CrossRefGoogle Scholar
Gurel-Gurevich, O. and Nachmias, A. (2013) Recurrence of planar graph limits. Ann. Math. (2) 177(2) 761–781.CrossRefGoogle Scholar
Győri, E., Paulos, A., Salia, N., Tompkins, C. and Zamora, O. (2019 a) The maximum number of paths of length three in a planar graph. arXiv:1909.13539.Google Scholar
Győri, E., Paulos, A., Salia, N., Tompkins, C. and Zamora, O. (2019 b) The maximum number of pentagons in a planar graph. arXiv:1909.13532.Google Scholar
Győri, E., Paulos, A., Salia, N., Tompkins, C. and Zamora, O. (2020) Generalized planar Turán numbers. arXiv:2002.04579v2.CrossRefGoogle Scholar
Győri, E., Salia, N., Tompkins, C. and Zamora, O. (2019) The maximum number of $P_\ell$ copies in $P_k$ -free graphs. Discrete Math. Theor. Comput. Sci. 21(1) #14.Google Scholar
Hakimi, S. L. and Schmeichel, E. F. (1979) On the number of cycles of length k in a maximal planar graph. J. Graph Theory 3(1) 69–86.CrossRefGoogle Scholar
Hakimi, S. L. and Schmeichel, E. F. (1982) Bounds on the number of cycles of length three in a planar graph. Israel J. Math. 41(1–2) 161–180.CrossRefGoogle Scholar
Harant, J., Horňák, M. and Skupień, Z. (2001) Separating 3-cycles in plane triangulations. Discrete Math. 239(1–3) 127–136.CrossRefGoogle Scholar
Hatami, H., Lovász, L. and Szegedy, B. (2014) Limits of locally-globally convergent graph sequences. Geom. Funct. Anal. 24(1) 269–296.CrossRefGoogle Scholar
Hatami, H. and Norine, S. Undecidability of linear inequalities in graph homomorphism densities. J. Am. Math. Soc. 24(2) 547–565 (2011).CrossRefGoogle Scholar
Huynh, T. and Wood, D. R. (2021) Tree densities in sparse graph classes. Canad. J. Math.CrossRefGoogle Scholar
Joret, G. and Wood, D. R. (2010) Irreducible triangulations are small. J. Comb. Theory Ser. B 100(5) 446–455.CrossRefGoogle Scholar
Lavrenchenko, S. (1987) Irreducible triangulations of a torus. Ukrain. Geom. Sb. 30 52–62, ii. Translation in J. Soviet Math. 51(5) 2537–2543 (1990).CrossRefGoogle Scholar
Lawrencenko, S. and Negami, S. (1997) Irreducible triangulations of the Klein bottle. J. Comb. Theory Ser. B 70(2) 265–291.CrossRefGoogle Scholar
Lee, C. and Oum, S.-i. (2015) Number of cliques in graphs with a forbidden subdivision. SIAM J. Discrete Math. 29(4) 1999–2005.CrossRefGoogle Scholar
Liu, C.-H. (2021) Homomorphism counts in robustly sparse graphs. arXiv:2107.00874.Google Scholar
Lovász, L. (2012) Large Networks and Graph Limits. Providence, USA: American Mathematical Society.CrossRefGoogle Scholar
Lovász, L. and Simonovits, M. (1976) On the number of complete subgraphs of a graph. In Proceedings of 5th British Combinatorial Conference, Vol. XV of Congressus Numerantium, Utilitas Mathematica, pp. 431–441.Google Scholar
Lovász, L. and Simonovits, M. (1983) On the number of complete subgraphs of a graph. II. In Studies in Pure Mathematics, BirkhÄuser, pp. 459–495.CrossRefGoogle Scholar
Luo, R. (2018) The maximum number of cliques in graphs without long cycles. J. Comb. Theory Ser. B 128 219–226.CrossRefGoogle Scholar
Ma, J. and Qiu, Y. (2020) Some sharp results on the generalized Turán numbers. Eur. J. Comb. 84 103026.CrossRefGoogle Scholar
Mantel, W. (1907) Problem 28. Wiskundige Opgaven 10 60–61.Google Scholar
Miller, G. L. (1987) An additivity theorem for the genus of a graph. J. Comb. Theory Ser. B 43(1) 25–47.CrossRefGoogle Scholar
Mohar, B. and Thomassen, C. (2001) Graphs on Surfaces. Johns Hopkins University Press.Google Scholar
Nakamoto, A. and Ota, K. (1995) Note on irreducible triangulations of surfaces. J. Graph Theory 20(2) 227–233.CrossRefGoogle Scholar
Nešetřil, J. and Ossona de Mendez, P. (2011) How many F’s are there in G? Eur. J. Comb. 32(7) 1126–1141.CrossRefGoogle Scholar
Nešetřil, J. and Ossona de Mendez, P. (2020) A unified approach to structural limits and limits of graphs with bounded tree-depth. Mem. Am. Math. Soc. 263(1272).Google Scholar
Nikiforov, V. (2011) The number of cliques in graphs of given order and size. Trans. Am. Math. Soc. 363(3) 1599–1618.CrossRefGoogle Scholar
Norine, S., Seymour, P., Thomas, R. and Wollan, P. (2006) Proper minor-closed families are small. J. Comb. Theory Ser. B 96(5) 754–757.CrossRefGoogle Scholar
Razborov, A. A. (2008) On the minimal density of triangles in graphs. Comb. Prob. Comput. 17(4) 603–618.CrossRefGoogle Scholar
Reed, B. and Wood, D. R. (2009) A linear time algorithm to find a separator in a graph excluding a minor. ACM Trans. Algorithms 5(4) #39.CrossRefGoogle Scholar
Reiher, C. (2016) The clique density theorem. Ann. Math. 184(3) 683–707.CrossRefGoogle Scholar
Ringel, G. (1974) Map Color Theorem. Springer-Verlag.CrossRefGoogle Scholar
Sulanke, T. (2006) Generating irreducible triangulations of surfaces. arXiv:0606687.Google Scholar
Sulanke, T. (2006) Irreducible triangulations of low genus surfaces. arXiv:0606690.Google Scholar
Sulanke, T. (2006) Note on the irreducible triangulations of the Klein bottle. J. Comb. Theory Ser. B 96(6) 964–972.CrossRefGoogle Scholar
Timmons, C. (2019) $C_{2k}$ -saturated graphs with no short odd cycles. Graphs Comb. 35(5) 1023–1034.CrossRefGoogle Scholar
Turán, P. (1941) On an extremal problem in graph theory. Mat. Fiz. Lapok 48 436–452.Google Scholar
Wood, D. R. (2007) On the maximum number of cliques in a graph. Graphs Comb. 23(3) 337–352.CrossRefGoogle Scholar
Wood, D. R. (2016) Cliques in graphs excluding a complete graph minor. Electr. J. Comb. 23(3) #R18.Google Scholar
Wormald, N. C. (1986) On the frequency of 3-connected subgraphs of planar graphs. Bull. Aust. Math. Soc. 34(2) 309–317.CrossRefGoogle Scholar
Zykov, A. A. (1949) On some properties of linear complexes. Mat. Sbornik N.S. 24(66) 163–188.Google Scholar