Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Füredi, Zoltán
1995.
Proceedings of the International Congress of Mathematicians.
p.
1343.
Carnielli, W.A
and
Monte Carmelo, E.L
1999.
On the Ramsey Problem for Multicolor Bipartite Graphs.
Advances in Applied Mathematics,
Vol. 22,
Issue. 1,
p.
48.
Alon, Noga
Rónyai, Lajos
and
Szabó, Tibor
1999.
Norm-Graphs: Variations and Applications.
Journal of Combinatorial Theory, Series B,
Vol. 76,
Issue. 2,
p.
280.
Axenovich, Maria
Füredi, Zoltán
and
Mubayi, Dhruv
2000.
On Generalized Ramsey Theory: The Bipartite Case.
Journal of Combinatorial Theory, Series B,
Vol. 79,
Issue. 1,
p.
66.
Yin, Jianhua
and
Li, Jiongsheng
2002.
The smallest degree sum that yields potentially Kr,r-graphic sequences.
Science China Mathematics,
Vol. 45,
Issue. 6,
p.
694.
Yin, Jian-Hua
Li, Jiong-Sheng
and
Chen, Guo-Liang
2004.
A variation of a classical Turán-type extremal problem.
European Journal of Combinatorics,
Vol. 25,
Issue. 7,
p.
989.
Keevash, Peter
Saks, Mike
Sudakov, Benny
and
Verstraëte, Jacques
2004.
Multicolour Turán problems.
Advances in Applied Mathematics,
Vol. 33,
Issue. 2,
p.
238.
Simonovits, Miklós
and
Sós, Vera T.
2005.
A hierarchy of randomness for graphs.
Discrete Mathematics,
Vol. 303,
Issue. 1-3,
p.
209.
Li, Yusheng
Tang, Xueqing
and
Zang, Wenan
2005.
Ramsey functions involvingKm,nwithnlarge.
Discrete Mathematics,
Vol. 300,
Issue. 1-3,
p.
120.
Shen, Jian
2006.
On two Turán Numbers.
Journal of Graph Theory,
Vol. 51,
Issue. 3,
p.
244.
Conlon, David
2008.
A new upper bound for the bipartite Ramsey problem.
Journal of Graph Theory,
Vol. 58,
Issue. 4,
p.
351.
Lin, Qizhong
and
Li, Yusheng
2009.
Bipartite Ramsey numbers involving large Kn,n.
European Journal of Combinatorics,
Vol. 30,
Issue. 4,
p.
923.
Sun, Yuqin
and
Li, Yusheng
2009.
Size bipartite Ramsey numbers.
Discrete Mathematics,
Vol. 309,
Issue. 5,
p.
1060.
Fujita, Shinya
Magnant, Colton
and
Ozeki, Kenta
2010.
Rainbow Generalizations of Ramsey Theory: A Survey.
Graphs and Combinatorics,
Vol. 26,
Issue. 1,
p.
1.
Bohman, Tom
and
Keevash, Peter
2010.
The early evolution of the H-free process.
Inventiones mathematicae,
Vol. 181,
Issue. 2,
p.
291.
Nikiforov, Vladimir
2010.
A contribution to the Zarankiewicz problem.
Linear Algebra and its Applications,
Vol. 432,
Issue. 6,
p.
1405.
Pettie, Seth
2011.
Degrees of nonlinearity in forbidden 0–1 matrix problems.
Discrete Mathematics,
Vol. 311,
Issue. 21,
p.
2396.
Blagojević, Pavle
Bukh, Boris
and
Karasev, Roman
2011.
Turán numbers for Ks,t-free graphs: topological obstructions and algebraic constructions.
Electronic Notes in Discrete Mathematics,
Vol. 38,
Issue. ,
p.
141.
Lin, Qizhong
and
Li, Yusheng
2011.
Multicolor bipartite Ramsey number of C4 and large Kn, n.
Journal of Graph Theory,
Vol. 67,
Issue. 1,
p.
47.
Balogh, József
and
Samotij, Wojciech
2011.
The number of K m,m -free graphs.
Combinatorica,
Vol. 31,
Issue. 2,
p.
131.

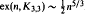 .
.