Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-28T10:34:38.764Z Has data issue: false hasContentIssue false
  • English
  • Français

Antidirected subgraphs of oriented graphs

Part of: Graph theory

Published online by Cambridge University Press:  06 March 2024

Maya Stein  and
Camila Zárate-Guerén
Maya Stein*
Affiliation:
Center for Mathematical Modeling (IRL CNRS 2807) and Department for Mathematical Engineering, University of Chile, Santiago, Chile
Camila Zárate-Guerén
Affiliation:
University of Birmingham, Birmingham, UK
*
Corresponding author: Maya Stein; Email: mstein@dim.uchile.cl
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for every 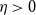$\eta \gt 0$ every sufficiently large $n$-vertex oriented graph 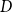$D$ of minimum semidegree exceeding 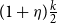$(1+\eta )\frac k2$ contains every balanced antidirected tree with 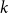$k$ edges and bounded maximum degree, if 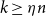$k\ge \eta n$. In particular, this asymptotically confirms a conjecture of the first author for long antidirected paths and dense digraphs.

Further, we show that in the same setting, 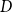$D$ contains every 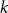$k$-edge antidirected subdivision of a sufficiently small complete graph, if the paths of the subdivision that have length 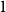$1$ or 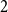$2$ span a forest. As a special case, we can find all antidirected cycles of length at most 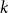$k$.

Finally, we address a conjecture of Addario-Berry, Havet, Linhares Sales, Reed, and Thomassé for antidirected trees in digraphs. We show that this conjecture is asymptotically true in $n$-vertex oriented graphs for all balanced antidirected trees of bounded maximum degree and of size linear in $n$.

Keywords

oriented graphtreesemidegreecyclepathsubdivisiondigraph

MSC classification

Primary: 05C20: Directed graphs (digraphs), tournaments
Secondary: 05C07: Vertex degrees 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , First View , pp. 1 - 21
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aboulker, P., Cohen, N., Havet, F., Lochet, W., Moura, P. F. S. and Thomassé, S. (2019) Sub- divisions in digraphs of large out-degree or large dichromatic number. Elect. J. Comb. 26(3) P3.19.CrossRefGoogle Scholar
Addario-Berry, L., Havet, F., Linhares Sales, C., Reed, B. and Thomassé, S. (2013) Oriented trees in digraphs. Discr. Math. 313(8) 967–974.CrossRefGoogle Scholar
Ajtai, M., Komlós, J. and Szemerédi, E. (1995) On a Conjecture of Loebl. In: Proceedings of the 7th International Conference on Graph Theory, Combinatorics, and Algorithms. Wiley, New York, pp. 1135–1146.Google Scholar
Alon, N. and Shapira, A. (2004) Testing subgraphs in directed graphs. J. Comput. Syst. Sci. 69(3) 354–382.CrossRefGoogle Scholar
Besomi, G., Pavez-Signé, M. and Stein, M. (2019) Degree conditions for embedding trees. SIAM J. Discr. Math. 33(3) 1521–1555.CrossRefGoogle Scholar
Besomi, G., Pavez-Signé, M. and Stein, M. (2020) Maximum and minimum degree conditions for embedding trees. SIAM J. Discr. Math. 34(4) 2108–2123.CrossRefGoogle Scholar
Burr, S. (1980) Subtrees of Directed Graphs and Hypergraphs. In:Proceedings of the Eleventh South- eastern Conference on Combinatorics, Graph Theory and Combinatorics Florida Atlantic University, Boca Raton, FL, pp. 227–239.Google Scholar
Cohen, N., Havet, F., Lochet, W. and Nisse, N. (2018) Subdivisions of oriented cycles in digraphs with large chromatic number. J. Graph Theor. 89(4) 439–456.CrossRefGoogle Scholar
Dirac, G. A. (1952) Some theorems on abstract graphs. Proc. London Math. Soc. s3-2(1) 69–81.CrossRefGoogle Scholar
Erdős, P. and Gallai, T. (1959) On maximal paths and circuits of graphs. Act Math Acad Sci Hung 10(3) 337–356.CrossRefGoogle Scholar
Girão, A., Popielarz, K. and Snyder, R. (2021) Subdivisions of digraphs in tournaments. J. Comb. Theory, Ser. B 146 266–285.CrossRefGoogle Scholar
Gishboliner, L., Steiner, R. and Szabó, T. (2022) Dichromatic number and forced subdivisions. J. Comb. Theory, Ser. B 153 1–30.CrossRefGoogle Scholar
Gishboliner, L., Steiner, R. and Szabó, T. (2022) Oriented cycles in digraphs of large outdegree. Combinatorica 42(1) 1145–1187.CrossRefGoogle Scholar
Graham, R. L. (1970) On subtrees of directed graphs with no path of length exceeding one. Canad. Math. Bull. 13(3) 329–332.CrossRefGoogle Scholar
Jackson, B. (1981) Long paths and cycles in oriented graphs. J. Graph Theor. 5(2) 145–157.CrossRefGoogle Scholar
Jagger, C. (1998) Extremal digraph results for topological complete tournaments. Eur. J. Combin. 19 687–694.CrossRefGoogle Scholar
Kathapurkar, A. and Montgomery, R. (2022) Spanning trees in dense directed graphs. J. Comb. Theory Ser. B 156 223–249.CrossRefGoogle Scholar
Keevash, P., Kühn, D. and Osthus, D. (2009) An exact minimum degree condition for Hamilton cycles in oriented graphs. J. Lond. Math. Soc. 79(1) 144–166.CrossRefGoogle Scholar
Kelly, L. (2011) Arbitrary Orientations of Hamilton Cycles in Oriented Graphs. Electron. J. Comb. 18(1) P186.CrossRefGoogle Scholar
Kelly, L., Kühn, D. and Osthus, D. (2008) A Dirac type result on Hamilton cycles in oriented graphs. Comb. Prob. Comp. 17(5) 689–709.Google Scholar
Kelly, L., Kühn, D. and Osthus, D. (2010) Cycles of given length in oriented graphs. J. Comb. Theory Ser. B 100(3) 251–264.CrossRefGoogle Scholar
Klimošová, T. and Stein, M. (2022) Antipaths in oriented graphs(In preparation).CrossRefGoogle Scholar
Komlós, J., Sárközy, G. N. and Szemerédi, E. (1995) Proof of a packing conjecture of Bollobás. Comb. Prob. Comp. 4(3) 241–255.CrossRefGoogle Scholar
Kühn, D., Osthus, D. and Young, A. (2008) A note on complete subdivisions in digraphs of large outdegree. J. Graph Theor. 57(1) 1–6.CrossRefGoogle Scholar
Mader, W. (1967) Homomorphieeigenschaften und mittlere Kantendichte von Graphen. Math. Ann. 174(4) 265–268.CrossRefGoogle Scholar
Mader, W. (1985) Degree and local connectivity in digraphs. Combinatorica 5(2) 161–165.CrossRefGoogle Scholar
Mycroft, R. and Naia, T. (2020) Trees and tree-like structures in dense digraphs. arXiv preprint: 2012.09201.Google Scholar
Scott, A. (2000) Subdivisions of Transitive Tournaments. Eur. J. Combin. 21(8) 1067–1071.CrossRefGoogle Scholar
Stein, M. (2021) Tree containment and degree conditions. In: Discrete Mathematics and Applications (Raigoroskii, A. and Rassias, M., eds), Springer, pp. 459–486.Google Scholar
Steiner, R. (2024) Subdivisions with congruence constraints in digraphs of large chromatic number. J. Graph Thr. 105(1) 136–143.CrossRefGoogle Scholar
Szemerédi, E. (1978) Regular partitions of graphs. Problémes Combinatoires et Théorie des Graphes Colloques Internationaux CNRS 260, 399–401.Google Scholar
Thomassen, C. (1985) Even cycles in directed graphs. Eur. J. Combin. 6(1) 85–89.CrossRefGoogle Scholar