Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-29T04:39:48.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximately symmetric forms far from being exactly symmetric

Part of: Algebraic combinatorics

Published online by Cambridge University Press:  18 October 2022

Luka Milićević Open the ORCID record for Luka Milićević [Opens in a new window]
Luka Milićević*
Affiliation:
Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade, Serbia
*
Email: luka.milicevic@turing.mi.sanu.ac.rs
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 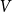$V$ be a finite-dimensional vector space over 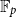$\mathbb{F}_p$ . We say that a multilinear form 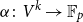$\alpha \colon V^k \to \mathbb{F}_p$ in 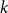$k$ variables is 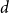$d$ -approximately symmetric if the partition rank of difference 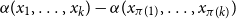$\alpha (x_1, \ldots, x_k) - \alpha (x_{\pi (1)}, \ldots, x_{\pi (k)})$ is at most 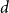$d$ for every permutation 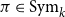$\pi \in \textrm{Sym}_k$ . In a work concerning the inverse theorem for the Gowers uniformity 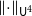$\|\!\cdot\! \|_{\mathsf{U}^4}$ norm in the case of low characteristic, Tidor conjectured that any 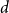$d$ -approximately symmetric multilinear form 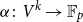$\alpha \colon V^k \to \mathbb{F}_p$ differs from a symmetric multilinear form by a multilinear form of partition rank at most 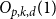$O_{p,k,d}(1)$ and proved this conjecture in the case of trilinear forms. In this paper, somewhat surprisingly, we show that this conjecture is false. In fact, we show that approximately symmetric forms can be quite far from the symmetric ones, by constructing a multilinear form 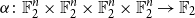$\alpha \colon \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \times \mathbb{F}_2^n \to \mathbb{F}_2$ which is 3-approximately symmetric, while the difference between 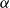$\alpha$ and any symmetric multilinear form is of partition rank at least 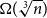$\Omega (\sqrt [3]{n})$ .

Keywords

Multilinear formsPartition rankSymmetric group

MSC classification

Primary: 05E18: Group actions on combinatorial structures
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 2 , March 2023 , pp. 299 - 315
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V., Tao, T. and Ziegler, T. (2010) An inverse theorem for the uniformity seminorms associated with the action of $\mathbb{F}^{\infty }_p$ . Geom. Funct. Anal. 19 1539–1596.CrossRefGoogle Scholar
Camarena, O. A. and Szegedy, B. (2010) Nilspaces, nilmanifolds and their morphisms. arXiv preprint, arXiv: 1009.3825.Google Scholar
Candela, P., González-Sánchez, D. and Szegedy, B. (2021) On higher-order Fourier analysis in characteristic $p$ . arXiv preprint, arXiv: 2109.15281.Google Scholar
Green, B. and Tao, T. (2008) An inverse theorem for the Gowers $U^3(G)$ -norm. Proc. Edinburgh Math. Soc. 51 73–153.CrossRefGoogle Scholar
Green, B., Tao, T. and Ziegler, T. (2012) An inverse theorem for the Gowers $U^{s+1}[N]$ -norm. Ann. Math. 176 1231–1372.CrossRefGoogle Scholar
Gowers, W. T. (2001) A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11 465–588.CrossRefGoogle Scholar
Gowers, W. T. and Milićević, L. (2017) A quantitative inverse theorem for the norm over finite fields. arXiv preprint, arXiv: 1712.00241.Google Scholar
Gowers, W. T. and Milićević, L. (2020) An inverse theorem for Freiman multi-homomorphisms. arXiv preprint, arXiv: 2002.11667.Google Scholar
Gutman, Y., Manners, F. and Varjú, P. (2020) The structure theory of Nilspaces I. J. Anal. Math. 140 299–369.CrossRefGoogle Scholar
Gutman, Y., Manners, F. and Varjú, P. (2019) The structure theory of Nilspaces II: Representation as nilmanifolds. Trans. Am. Math. Soc. 371 4951–4992.CrossRefGoogle Scholar
Gutman, Y., Manners, F. and Varjú, P. (2020) The structure theory of Nilspaces III: Inverse limit representations and topological dynamics. Adv. Math. 365 107059.CrossRefGoogle Scholar
Jamneshan, A. and Tao, T. (2021) The inverse theorem for the Gowers uniformity norm on arbitrary finite abelian groups: Fourier-analytic and ergodic approaches. arXiv preprint, arXiv: 2112.13759.Google Scholar
Janzer, O. (2020) Polynomial bound for the partition rank vs the analytic rank of tensors. Discrete Anal., 1–18, paper no. 7.Google Scholar
Manners, F. (2018) Quantitative bounds in the inverse theorem for the Gowers-norms over cyclic groups. arXiv preprint, arXiv: 1811.00718.Google Scholar
Milićević, L. (2019) Polynomial bound for partition rank in terms of analytic rank. Geom. Funct. Anal. 29 1503–1530.Google Scholar
Milićević, L. (2022) Quantitative inverse theorem for Gowers uniformity norms $\mathsf{U}^5$ and $\mathsf{U}^6$ in. arXiv preprint, arXiv: 2207.01591.Google Scholar
Naslund, E. (2020) The partition rank of a tensor and $k$ -right corners in $\mathbb{F}_q^n$ . J. Comb. Theory Ser. A 174 article–105190.Google Scholar
Samorodnitsky, A. (2007) Low-degree tests at large distances. In STOC’07-Proceedings of the 39 $^{th}$ Annual ACM Symposium on Theory of Computing, ACM, New York, pp. 506–515.CrossRefGoogle Scholar
Szegedy, B. (2012) On higher order Fourier analysis. arXiv preprint, arXiv: 1203.2260.Google Scholar
Tao, T. and Ziegler, T. (2012) The inverse conjecture for the Gowers norm over finite fields in low characteristic. Ann. Comb. 16 121–188.CrossRefGoogle Scholar
Tidor, J. (2021) Quantitative bounds for the $U^4$ -inverse theorem over low characteristic finite fields. arXiv preprint, arXiv: 2109.13108.Google Scholar