Hostname: page-component-5db58dd55d-qmkzp Total loading time: 0 Render date: 2026-05-30T23:23:57.970Z Has data issue: false hasContentIssue false
  • English
  • Français

Bootstrap Percolation in High Dimensions

Published online by Cambridge University Press:  12 August 2010

JÓZSEF BALOGH ,
BÉLA BOLLOBÁS  and
ROBERT MORRIS
JÓZSEF BALOGH
Affiliation:
Department of Mathematics, University of Illinois, 1409 W. Green Street, Urbana, IL 61801 and Department of Mathematics, University of California, San Diego, La Jolla, CA 92093 (e-mail: jobal@math.uiuc.edu)
BÉLA BOLLOBÁS
Affiliation:
Trinity College, Cambridge CB2 1TQ, England and Department of Mathematical Sciences, The University of Memphis, Memphis, TN 38152, USA (e-mail: B.Bollobas@dpmms.cam.ac.uk)
ROBERT MORRIS
Affiliation:
IMPA, Estrada Dona Castorina 110, Jardim Botânico, Rio de Janeiro, RJ, Brasil (e-mail: rob@impa.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

In r-neighbour bootstrap percolation on a graph G, a set of initially infected vertices A ⊂ V(G) is chosen independently at random, with density p, and new vertices are subsequently infected if they have at least r infected neighbours. The set A is said to percolate if eventually all vertices are infected. Our aim is to understand this process on the grid, [n]d, for arbitrary functions n = n(t), d = d(t) and r = r(t), as t → ∞. The main question is to determine the critical probability pc([n]d, r) at which percolation becomes likely, and to give bounds on the size of the critical window. In this paper we study this problem when r = 2, for all functions n and d satisfying d ≫ log n.

The bootstrap process has been extensively studied on [n]d when d is a fixed constant and 2 ⩽ r ⩽ d, and in these cases pc([n]d, r) has recently been determined up to a factor of 1 + o(1) as n → ∞. At the other end of the scale, Balogh and Bollobás determined pc([2]d, 2) up to a constant factor, and Balogh, Bollobás and Morris determined pc([n]d, d) asymptotically if d ≥ (log log n)2+ϵ, and gave much sharper bounds for the hypercube.

Here we prove the following result. Let λ be the smallest positive root of the equation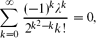so λ ≈ 1.166. Then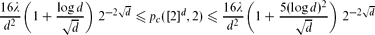if d is sufficiently large, and moreover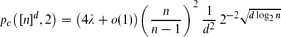as d → ∞, for every function n = n(d) with d ≫ log n.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Adler, J. and Lev, U. (2003) Bootstrap percolation: Visualizations and applications. Braz. J. Phys. 33 641–644.CrossRefGoogle Scholar
[2]Aizenman, M. and Lebowitz, J. L. (1988) Metastability effects in bootstrap percolation. J. Phys. A 21 3801–3813.CrossRefGoogle Scholar
[3]Ajtai, M., Komlós, J. and Szemerédi, E. (1982) Largest random component of a k-cube. Combinatorica 2 1–7.CrossRefGoogle Scholar
[4]Balogh, J. and Bollobás, B. (2006) Bootstrap percolation on the hypercube. Probab. Theory Rel. Fields 134 624–648.Google Scholar
[5]Balogh, J., Bollobás, B., Duminil-Copin, H. and Morris, R. The sharp threshold for bootstrap percolation in all dimensions. In preparation.Google Scholar
[6]Balogh, J., Bollobás, B. and Morris, R. (2009) Majority bootstrap percolation on the hypercube. Combin. Probab. Comput. 18 17–51.Google Scholar
[7]Balogh, J., Bollobás, B. and Morris, R. (2009) Bootstrap percolation in three dimensions. Ann. Probab. 37 1329–1380.CrossRefGoogle Scholar
[8]Balogh, J., Bollobás, B. and Morris, R. Bootstrap percolation in high dimensions. Manuscript: arXiv:0907.3097.Google Scholar
[9]Balogh, J., Peres, Y. and Pete, G. (2006) Bootstrap percolation on infinite trees and non-amenable groups. Combin. Probab. Comput. 15 715–730.CrossRefGoogle Scholar
[10]Balogh, J. and Pittel, B. (2007) Bootstrap percolation on random regular graphs. Random Struct. Alg. 30 257–286.CrossRefGoogle Scholar
[11]van den Berg, J. and Kesten, H. (1985) Inequalities with applications to percolation and reliability. J. Appl. Probab. 22 556–589.Google Scholar
[12]Bollobás, B. (2001) Random Graphs, 2nd edn, Cambridge University Press.Google Scholar
[13]Bollobás, B., Kohayakawa, Y. and Łuczak, T. (1992) The evolution of random subgraphs of the cube. Random Struct. Alg. 3 55–90.Google Scholar
[14]Borgs, C., Chayes, J. T., van der Hofstad, R., Slade, G. and Spencer, J. (2006) Random subgraphs of finite graphs III: The phase transition for the n-cube. Combinatorica 26 395–410.Google Scholar
[15]Cerf, R. and Cirillo, E. N. M. (1999) Finite size scaling in three-dimensional bootstrap percolation. Ann. Probab. 27 1837–1850.CrossRefGoogle Scholar
[16]Cerf, R. and Manzo, F. (2002) The threshold regime of finite volume bootstrap percolation. Stochastic Proc. Appl. 101 69–82.Google Scholar
[17]Chalupa, J., Leath, P. L. and Reich, G. R. (1979) Bootstrap percolation on a Bethe lattice. J. Phys. C 12 L31–L35.Google Scholar
[18]Duminil-Copin, H. and Holroyd, A. Sharp metastability for threshold growth models. In preparation.Google Scholar
[19]Erdős, P. and Hanani, H. (1963) On a limit theorem in combinatorial analysis. Publ. Math. Debrecen 10 10–13.Google Scholar
[20]Erdős, P. and Spencer, J. (1979) Evolution of the n-cube. Comput. Math. Appl. 5 33–39.CrossRefGoogle Scholar
[21]Fontes, L. R. and Schonmann, R. H. (2008) Bootstrap percolation on homogeneous trees has 2 phase transitions. J. Statist. Phys. 132 839–861.CrossRefGoogle Scholar
[22]Fontes, L. R., Schonmann, R. H. and Sidoravicius, V. (2002) Stretched exponential fixation in stochastic Ising models at zero temperature. Commun. Math. Phys. 228 495–518.Google Scholar
[23]Gravner, J., Holroyd, A. and Morris, R. A sharper threshold for bootstrap percolation in two dimensions. Submitted.Google Scholar
[24]van der Hofstad, R. and Slade, G. (2005) Asymptotic expansion in n −1 for percolation critical values on the n-cube and ℤn. Random Struct. Alg. 27 331–357.Google Scholar
[25]van der Hofstad, R. and Slade, G. (2006) Expansion in n −1 for percolation critical values on the n-cube and ℤn: the first three terms. Combin. Probab. Comput. 15 695–713.Google Scholar
[26]Holroyd, A. (2003) Sharp metastability threshold for two-dimensional bootstrap percolation. Probab. Theory Rel. Fields 125 195–224.CrossRefGoogle Scholar
[27]Janson, S. (2009) On percolation in random graphs with given vertex degrees. Electronic J. Probab. 14 Paper 5, 86–118.Google Scholar
[28]Morris, R. Zero-temperature Glauber dynamics on ℤd. Probab. Theory Rel. Fields, to appear.Google Scholar
[29]Nanda, S., Newman, C. M. and Stein, D. (2000) Dynamics of Ising spin systems at zero temperature. In On Dobrushin's Way: From Probability Theory to Statistical Mechanics (Minlos, R., Shlosman, S. and Suhov, Y., eds), Vol. 198 of Amer. Math. Soc. Transl. Ser. 2, AMS, pp. 183–194.Google Scholar
[30]Newman, C. M. and Stein, D. (2000) Zero-temperature dynamics of Ising spin systems following a deep quench: Results and open problems. Physica A 279 159–168.Google Scholar
[31]Pete, G. (1998) Disease processes and bootstrap percolation. Thesis for Diploma at the Bolyai Institute, József Attila University, Szeged, Hungary.Google Scholar
[32]Rödl, V. (1985) On a packing and covering problem. Europ. J. Combin. 6 69–78.Google Scholar
[33]Schonmann, R. H. (1992) On the behaviour of some cellular automata related to bootstrap percolation. Ann. Probab. 20 174–193.Google Scholar