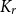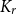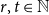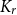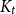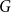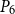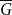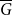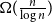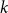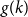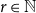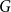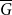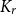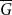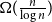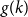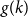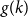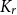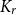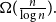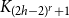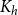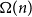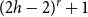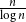1. Introduction
1.1. Overview
The extremal number of a graph
![]() $H,$
denoted by
$H,$
denoted by
![]() $\mathrm{ex}(n, H)$
, is the maximum number of edges in an
$\mathrm{ex}(n, H)$
, is the maximum number of edges in an
![]() $n$
-vertex graph with no copy of
$n$
-vertex graph with no copy of
![]() $H$
. Its historical roots trace back to Mantel’s result from
$H$
. Its historical roots trace back to Mantel’s result from
![]() $1907$
[Reference Mantel25], showing that
$1907$
[Reference Mantel25], showing that
![]() ${\rm{ex}}(n,{K_3}) = \lfloor {{{{n^2}} \over 4}} \rfloor .$
This was generalised by Turán [Reference Turán35] who determined
${\rm{ex}}(n,{K_3}) = \lfloor {{{{n^2}} \over 4}} \rfloor .$
This was generalised by Turán [Reference Turán35] who determined
![]() $\mathrm{ex}(n, K_r)$
for all
$\mathrm{ex}(n, K_r)$
for all
![]() $r$
. Later, the Erdős–Stone–Simonovits theorem [Reference Erdős and Simonovits9, Reference Erdős and Stone10] asserts that
$r$
. Later, the Erdős–Stone–Simonovits theorem [Reference Erdős and Simonovits9, Reference Erdős and Stone10] asserts that
![]() ${\rm{ex}}(n,H) = (1 - \frac{1}{\chi (H)-1}+ o(1))\binom{n}{2}$
, which asymptotically determines
${\rm{ex}}(n,H) = (1 - \frac{1}{\chi (H)-1}+ o(1))\binom{n}{2}$
, which asymptotically determines
![]() $\mathrm{ex}(n, H)$
for any graph
$\mathrm{ex}(n, H)$
for any graph
![]() $H$
that is not bipartite. The Erdős–Stone–Simonovits theorem is widely considered as ‘the fundamental theorem of extremal graph theory’. This was strengthened by Bollobás, Erdős, and Simonovits [Reference Bollobás, Erdős and Simonovits5] as follows. Denote by
$H$
that is not bipartite. The Erdős–Stone–Simonovits theorem is widely considered as ‘the fundamental theorem of extremal graph theory’. This was strengthened by Bollobás, Erdős, and Simonovits [Reference Bollobás, Erdős and Simonovits5] as follows. Denote by
![]() $\varrho _r(G)$
the
$\varrho _r(G)$
the
![]() $K_r$
-density of
$K_r$
-density of
![]() $G$
, which is the number of copies of
$G$
, which is the number of copies of
![]() $K_r$
in
$K_r$
in
![]() $G$
normalised by
$G$
normalised by
![]() $\binom{|G|}{r}$
. For a graph
$\binom{|G|}{r}$
. For a graph
![]() $H$
, we denote by
$H$
, we denote by
![]() $H[t]$
the
$H[t]$
the
![]() $t$
-blowup of
$t$
-blowup of
![]() $H$
obtained by replacing every vertex of
$H$
obtained by replacing every vertex of
![]() $H$
by an independent set of size
$H$
by an independent set of size
![]() $t$
and every edge of
$t$
and every edge of
![]() $H$
by a copy of
$H$
by a copy of
![]() $K_{t,t}$
. It was shown [Reference Bollobás, Erdős and Simonovits5] that every
$K_{t,t}$
. It was shown [Reference Bollobás, Erdős and Simonovits5] that every
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with edge density
$G$
with edge density
![]() ${\varrho _2}(G)1 - {1 \over {r - 1}} + \varepsilon $
contains a complete
${\varrho _2}(G)1 - {1 \over {r - 1}} + \varepsilon $
contains a complete
![]() $r$
-partite subgraph
$r$
-partite subgraph
![]() $K_{r}[\varepsilon ^{r}\log {n}]$
. By considering random graphs of the same edge density, we see that the logarithmic dependence on
$K_{r}[\varepsilon ^{r}\log {n}]$
. By considering random graphs of the same edge density, we see that the logarithmic dependence on
![]() $n$
is optimal.
$n$
is optimal.
Given that random graphs are highly unstructured, it seems natural to ask whether larger blowups of cliques can be found in graphs from special families. We focus on finding largest possible blowups – those of sizes almost linear in the order of
![]() $G$
. Recently, there have been various results of this type under edge density conditions. For instance, Fox, Pach, and Tóth [Reference Fox, Pach and Tóth17] showed that any
$G$
. Recently, there have been various results of this type under edge density conditions. For instance, Fox, Pach, and Tóth [Reference Fox, Pach and Tóth17] showed that any
![]() $n$
-vertex incomparability graph
$n$
-vertex incomparability graph
![]() $G$
with
$G$
with
![]() $\varrho _2(G)\gt 0$
contains a
$\varrho _2(G)\gt 0$
contains a
![]() $K_2[t]$
with
$K_2[t]$
with
![]() $t = \Omega ({n \over {\log n}}).$
Tomon [Reference Tomon34] proved that the complement of an
$t = \Omega ({n \over {\log n}}).$
Tomon [Reference Tomon34] proved that the complement of an
![]() $n$
-vertex string graph
$n$
-vertex string graph
![]() $G$
with
$G$
with
![]() ${\varrho _2}(G){\gt}{3 \over 4}$
contains a
${\varrho _2}(G){\gt}{3 \over 4}$
contains a
![]() $K_{2}[t]$
with
$K_{2}[t]$
with
![]() $t=\Omega (n)$
. Apart from these recent developments, the Ramsey problem of finding a biclique of linear size in a graph or its complement also receives a great deal of attention [Reference Cho, Holmsen, Kim and Kim6, Reference Fox, Pach and Tóth17, Reference Fu19], as it is closely related to the Erdős–Hajnal conjecture [Reference Erdős and Hajnal8].
$t=\Omega (n)$
. Apart from these recent developments, the Ramsey problem of finding a biclique of linear size in a graph or its complement also receives a great deal of attention [Reference Cho, Holmsen, Kim and Kim6, Reference Fox, Pach and Tóth17, Reference Fu19], as it is closely related to the Erdős–Hajnal conjecture [Reference Erdős and Hajnal8].
In a different direction, a beautiful strengthening of the Bollobás–Erdős–Simonovits theorem by Nikiforov [Reference Nikiforov27] replaces the edge density condition by a weaker clique density condition. More precisely, by the so-called supersaturation result of Erdős and Simonovits [Reference Erdős and Simonovits11], any graph with
![]() ${\varrho _2}(G) \gt 1 - {1 \over {r - 1}}$
not only contains a single
${\varrho _2}(G) \gt 1 - {1 \over {r - 1}}$
not only contains a single
![]() $r$
-clique, but has positive
$r$
-clique, but has positive
![]() $K_r$
-density
$K_r$
-density
![]() $\varrho _r(G)\gt 0$
. Nikiforov [Reference Nikiforov27] showed that a graph having
$\varrho _r(G)\gt 0$
. Nikiforov [Reference Nikiforov27] showed that a graph having
![]() $\varrho _r(G)\gt 0$
already suffices to imply a logarithmic blowup of
$\varrho _r(G)\gt 0$
already suffices to imply a logarithmic blowup of
![]() $K_r$
.
$K_r$
.
In this work we combine the above two directions of extensions to find large blowups of cliques in some well-known classes of graphs with clique density conditions instead of edge density. More precisely, we study the following general question.
Question A.
Given a graph class
![]() $\mathcal{G}$
and
$\mathcal{G}$
and
![]() $t\in \mathbb{N}$
, find the minimum
$t\in \mathbb{N}$
, find the minimum
![]() $r\in \mathbb{N}$
such that if any
$r\in \mathbb{N}$
such that if any
![]() $G \in \mathcal{G}$
has positive
$G \in \mathcal{G}$
has positive
![]() $K_r$
-density
$K_r$
-density
![]() $\varrho _r(G)\gt 0$
, then
$\varrho _r(G)\gt 0$
, then
![]() $G$
contains a near-linear-sized blowup of
$G$
contains a near-linear-sized blowup of
![]() $K_t$
?
$K_t$
?
1.2. Our contributions
1.2.1. Ordered graphs forbidding monotone induced path
An ordered graph
![]() $G_{\lt }$
is a graph with a total ordering
$G_{\lt }$
is a graph with a total ordering
![]() $\lt$
on its vertex set
$\lt$
on its vertex set
![]() $V(G)$
. We say
$V(G)$
. We say
![]() $H_{\lt }$
is an induced ordered subgraph of
$H_{\lt }$
is an induced ordered subgraph of
![]() $G_{\lt }$
if there exists an order and adjacency preserving map from
$G_{\lt }$
if there exists an order and adjacency preserving map from
![]() $V(H)$
to
$V(H)$
to
![]() $V(G),$
i.e. there exists
$V(G),$
i.e. there exists
![]() $f\,:\,V(H)\rightarrow V(G)$
such that for each pair
$f\,:\,V(H)\rightarrow V(G)$
such that for each pair
![]() $u,v\in V(H)$
, if
$u,v\in V(H)$
, if
![]() $u\lt v$
then
$u\lt v$
then
![]() $f(u)\lt f(v)$
, and
$f(u)\lt f(v)$
, and
![]() $uv\in E(H)$
if and only if
$uv\in E(H)$
if and only if
![]() $f(u)f(v)\in E(G)$
. For extremal problems concerning ordered graphs, we refer the reader to some of the recent work [Reference Balko, Jelínek and Valtr2, Reference Conlon, Fox, Lee and Sudakov7, Reference Korándi, Tardos, Tomon and Weidert23, Reference Methuku and Tomon26, Reference Pach and Tardos28] and the references therein.
$f(u)f(v)\in E(G)$
. For extremal problems concerning ordered graphs, we refer the reader to some of the recent work [Reference Balko, Jelínek and Valtr2, Reference Conlon, Fox, Lee and Sudakov7, Reference Korándi, Tardos, Tomon and Weidert23, Reference Methuku and Tomon26, Reference Pach and Tardos28] and the references therein.
Ordered graphs have close connections to geometrically defined graphs. Often, much better quantitative Ramsey results hold for graphs arising from geometric settings. For instance, Fox, Pach, and Tóth [Reference Fox, Pach and Tóth17] proved that for any
![]() $n$
-vertex intersection graph
$n$
-vertex intersection graph
![]() $G$
of
$G$
of
![]() $x$
-monotone curves in the plane, either
$x$
-monotone curves in the plane, either
![]() $G$
contains a
$G$
contains a
![]() ${K_2}[{{cn} \over {\log n}}]$
or its complement
${K_2}[{{cn} \over {\log n}}]$
or its complement
![]() $\overline {G}$
contains a
$\overline {G}$
contains a
![]() $K_{2}[cn]$
for some
$K_{2}[cn]$
for some
![]() $c\gt 0$
. The original proof in [Reference Fox, Pach and Tóth17] heavily relies on the geometric nature of the
$c\gt 0$
. The original proof in [Reference Fox, Pach and Tóth17] heavily relies on the geometric nature of the
![]() $x$
-monotone curves. Recently, Pach and Tomon [Reference Pach and Tomon29] provided a simpler combinatorial proof using ordered graphs. A monotone path
$x$
-monotone curves. Recently, Pach and Tomon [Reference Pach and Tomon29] provided a simpler combinatorial proof using ordered graphs. A monotone path
![]() $P_{k}$
is an ordered graph with
$P_{k}$
is an ordered graph with
![]() $k$
vertices
$k$
vertices
![]() $v_{1}\lt v_{2}\lt \cdots \lt v_{k}$
in which
$v_{1}\lt v_{2}\lt \cdots \lt v_{k}$
in which
![]() $v_{i}$
and
$v_{i}$
and
![]() $v_{j}$
are adjacent if and only if
$v_{j}$
are adjacent if and only if
![]() $|i-j|=1$
. A key ingredient in their proof is the following result.
$|i-j|=1$
. A key ingredient in their proof is the following result.
Theorem 1.1 (Pach–Tomon [Reference Pach and Tomon29]). For every
![]() $k\geqslant 3$
, there exists
$k\geqslant 3$
, there exists
![]() $0\leqslant \beta (k)\lt 1$
such that the following holds. Let
$0\leqslant \beta (k)\lt 1$
such that the following holds. Let
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $G=G_{\lt }$
be an
$G=G_{\lt }$
be an
![]() $n$
-vertex ordered graph with no induced monotone path
$n$
-vertex ordered graph with no induced monotone path
![]() $P_{k}$
and its complement satisfies
$P_{k}$
and its complement satisfies
![]() $\delta (\overline {G})\geqslant (\beta (k)+\varepsilon )n$
. Then
$\delta (\overline {G})\geqslant (\beta (k)+\varepsilon )n$
. Then
![]() $\overline {G}$
contains a copy of
$\overline {G}$
contains a copy of
![]() ${K_2}[{{cn} \over {\log n}}]$
, where
${K_2}[{{cn} \over {\log n}}]$
, where
![]() $c=c(\varepsilon )\gt 0$
.
$c=c(\varepsilon )\gt 0$
.
Here
![]() $\delta (G)$
stands for the minimum degree of
$\delta (G)$
stands for the minimum degree of
![]() $G$
. This theorem generalises the result of Fox, Pach, and Tóth [Reference Fox, Pach and Tóth17] who proved it for the case
$G$
. This theorem generalises the result of Fox, Pach, and Tóth [Reference Fox, Pach and Tóth17] who proved it for the case
![]() $k=3$
(in this case
$k=3$
(in this case
![]() $G$
is a comparability graph) with the optimal constant
$G$
is a comparability graph) with the optimal constant
![]() $\beta (3)=0$
(see Theorem 1.5). It remains an open problem to determine the optimal value of
$\beta (3)=0$
(see Theorem 1.5). It remains an open problem to determine the optimal value of
![]() $\beta (k)$
for larger
$\beta (k)$
for larger
![]() $k$
. When
$k$
. When
![]() $k=5$
, Pach and Tomon [Reference Pach and Tomon29] provided the following example showing that
$k=5$
, Pach and Tomon [Reference Pach and Tomon29] provided the following example showing that
![]() $\beta (5)\geqslant 1/2$
. Take the union of two disjoint cliques on
$\beta (5)\geqslant 1/2$
. Take the union of two disjoint cliques on
![]() $[n/2]$
and
$[n/2]$
and
![]() $[n]{\setminus} [n/2]$
respectively and add cross edges randomly and independently with probability
$[n]{\setminus} [n/2]$
respectively and add cross edges randomly and independently with probability
![]() $\varepsilon \gt 0$
. The resulting graph
$\varepsilon \gt 0$
. The resulting graph
![]() $G$
has no induced monotone
$G$
has no induced monotone
![]() $P_5$
and with high probability
$P_5$
and with high probability
![]() $\delta (\overline {G})\geqslant (1/2 - \varepsilon )n$
, but the maximum size of a biclique in
$\delta (\overline {G})\geqslant (1/2 - \varepsilon )n$
, but the maximum size of a biclique in
![]() $\overline {G}$
is
$\overline {G}$
is
![]() $O_{\varepsilon }(\log n)$
.
$O_{\varepsilon }(\log n)$
.
We confirm that the above construction is optimal, i.e.,
![]() $\beta (5)=1/2$
. In fact, we prove it in a stronger form, showing that rather than the edge density condition as in Theorem 1.1, large blowups originates from having positive triangle density.
$\beta (5)=1/2$
. In fact, we prove it in a stronger form, showing that rather than the edge density condition as in Theorem 1.1, large blowups originates from having positive triangle density.
Theorem 1.2.
Let
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $G=G_{\lt }$
be an
$G=G_{\lt }$
be an
![]() $n$
-vertex ordered graph with no induced monotone path
$n$
-vertex ordered graph with no induced monotone path
![]() $P_{5}$
and
$P_{5}$
and
![]() $\varrho _3(\overline {G})\gt \varepsilon$
. Then
$\varrho _3(\overline {G})\gt \varepsilon$
. Then
![]() $\overline {G}$
contains a copy of
$\overline {G}$
contains a copy of
![]() ${K_2}[{{cn} \over {\log n}}]$
, where
${K_2}[{{cn} \over {\log n}}]$
, where
![]() $c=c(\varepsilon )\gt 0$
.
$c=c(\varepsilon )\gt 0$
.
It is worth pointing out that this theme of ‘replacing edge density by clique density’ not only reveals the real cause of the phenomenon occurred (here being the appearance of large biclique), but also implies the stability result for the edge density version. Indeed, if an
![]() $n$
-vertex ordered graph with no induced monotone
$n$
-vertex ordered graph with no induced monotone
![]() $P_5$
has edge density close to
$P_5$
has edge density close to
![]() $1/2$
and no biclique of size
$1/2$
and no biclique of size
![]() $\Omega ({n \over {\log n}})$
, then by Theorem 1.2 it must have zero triangle density. Thus, it follows from the classical Erdős–Simonovits stability result [Reference Erdős and Simonovits9] that the graph
$\Omega ({n \over {\log n}})$
, then by Theorem 1.2 it must have zero triangle density. Thus, it follows from the classical Erdős–Simonovits stability result [Reference Erdős and Simonovits9] that the graph
![]() $G$
must be close to balanced complete bipartite graph.
$G$
must be close to balanced complete bipartite graph.
By considering the union of
![]() $s$
disjoint
$s$
disjoint
![]() ${n \over s}$
-cliques and adding random edges between distinct cliques, we see that
${n \over s}$
-cliques and adding random edges between distinct cliques, we see that
![]() $\beta (2s + 1)\geqslant 1 - {1 \over s}$
. After seeing Theorem 1.2, it is tempting to believe that for an induced monotone
$\beta (2s + 1)\geqslant 1 - {1 \over s}$
. After seeing Theorem 1.2, it is tempting to believe that for an induced monotone
![]() $P_{2s+1}$
-free
$P_{2s+1}$
-free
![]() $G$
, positive
$G$
, positive
![]() $K_{s+1}$
-density in
$K_{s+1}$
-density in
![]() $\overline {G}$
forces a large biclique in
$\overline {G}$
forces a large biclique in
![]() $\overline {G}$
. Much to our own surprise, this is already false for the next case when forbidding
$\overline {G}$
. Much to our own surprise, this is already false for the next case when forbidding
![]() $P_7$
! It turns out that we need a positive
$P_7$
! It turns out that we need a positive
![]() $K_5$
-density.
$K_5$
-density.
Theorem 1.3.
For any
![]() $\varepsilon \gt 0$
and an
$\varepsilon \gt 0$
and an
![]() $n$
-vertex ordered graph
$n$
-vertex ordered graph
![]() $G=G_{\lt }$
with no induced monotone
$G=G_{\lt }$
with no induced monotone
![]() $P_{7}$
, if
$P_{7}$
, if
![]() $\varrho _5(\overline {G})\gt \varepsilon$
, then
$\varrho _5(\overline {G})\gt \varepsilon$
, then
![]() $\overline {G}$
contains a copy of
$\overline {G}$
contains a copy of
![]() ${K_2}[{{cn} \over {\log n}}]$
, where
${K_2}[{{cn} \over {\log n}}]$
, where
![]() $c=c(\varepsilon )\gt 0$
.
$c=c(\varepsilon )\gt 0$
.
On the other hand, there are
![]() $n$
-vertex ordered graphs
$n$
-vertex ordered graphs
![]() $G$
with no induced monotone path
$G$
with no induced monotone path
![]() $P_{7}$
,
$P_{7}$
,
![]() $\varrho _4(\overline {G})\gt 0$
and no biclique of size
$\varrho _4(\overline {G})\gt 0$
and no biclique of size
![]() $n/e^{o(\sqrt {\log n/\log \log n})}$
in
$n/e^{o(\sqrt {\log n/\log \log n})}$
in
![]() $\overline {G}$
.
$\overline {G}$
.
Theorems 1.2 and 1.3 are special cases of our main result. To state it, let
![]() $g(k)$
be the minimum
$g(k)$
be the minimum
![]() $r\in \mathbb{N}$
such that if any
$r\in \mathbb{N}$
such that if any
![]() $n$
-vertex ordered graph
$n$
-vertex ordered graph
![]() $G$
with no induced monotone
$G$
with no induced monotone
![]() $P_{2k}$
satisfies
$P_{2k}$
satisfies
![]() $\varrho _r(\overline {G})\gt 0$
, then
$\varrho _r(\overline {G})\gt 0$
, then
![]() $\overline {G}$
contains a copy of
$\overline {G}$
contains a copy of
![]() ${K_2}[\Omega ({n \over {\log n}})]$
. We in fact prove
${K_2}[\Omega ({n \over {\log n}})]$
. We in fact prove
![]() $g(3)=3$
and
$g(3)=3$
and
![]() $g(4)=5$
, which imply Theorems 1.2 and 1.3 (with the weaker
$g(4)=5$
, which imply Theorems 1.2 and 1.3 (with the weaker
![]() $P_6$
-free or
$P_6$
-free or
![]() $P_8$
-free condition). For general
$P_8$
-free condition). For general
![]() $k$
, although the construction showing
$k$
, although the construction showing
![]() $\beta (2s + 1)\geqslant 1 - {1 \over s}$
is not optimal, it is not inconceivable that
$\beta (2s + 1)\geqslant 1 - {1 \over s}$
is not optimal, it is not inconceivable that
![]() $g(k)$
is linear in
$g(k)$
is linear in
![]() $k$
. However, we show that the growth rate of
$k$
. However, we show that the growth rate of
![]() $g(k)$
is rather quadratic, determining
$g(k)$
is rather quadratic, determining
![]() $g(k)$
up to a factor of 2.
$g(k)$
up to a factor of 2.
Our main result reads as follows.
Theorem 1.4.
For
![]() $k \geqslant 3$
, we have
$k \geqslant 3$
, we have
![]() $\lfloor {{{{k^2}} \over 4}} \rfloor \lt g(k) \leqslant {{{k^2} - k + 2} \over 2}$
. That is, the followings hold.
$\lfloor {{{{k^2}} \over 4}} \rfloor \lt g(k) \leqslant {{{k^2} - k + 2} \over 2}$
. That is, the followings hold.
-
• For any
 $\varepsilon \gt 0$
and an
$\varepsilon \gt 0$
and an
 $n$
-vertex ordered graph
$n$
-vertex ordered graph
 $G = G_\lt$
with no induced monotone
$G = G_\lt$
with no induced monotone
 $P_{2k}$
, if
$P_{2k}$
, if
 $\varrho _{r}(\overline {G})\gt \varepsilon$
, where
$\varrho _{r}(\overline {G})\gt \varepsilon$
, where
 $r = {{{k^2} - k + 2} \over 2}$
, then
$r = {{{k^2} - k + 2} \over 2}$
, then
 $\overline {G}$
contains a copy of
$\overline {G}$
contains a copy of
 ${K_2}[{{cn} \over {\log n}}]$
, where
${K_2}[{{cn} \over {\log n}}]$
, where
 $c=c(\varepsilon )\gt 0$
.
$c=c(\varepsilon )\gt 0$
. -
• On the other hand, there are
 $n$
-vertex ordered graphs
$n$
-vertex ordered graphs
 $G$
with no induced monotone path
$G$
with no induced monotone path
 $P_{2k-1}$
,
$P_{2k-1}$
,
 ${\varrho _{\lfloor {{{{k^2}} \over 4}} \rfloor }}(\bar G)\gt 0$
and no biclique of size
${\varrho _{\lfloor {{{{k^2}} \over 4}} \rfloor }}(\bar G)\gt 0$
and no biclique of size
 $n/{e^{o(\sqrt {\log n/\log \log n} )}}$
in
$n/{e^{o(\sqrt {\log n/\log \log n} )}}$
in
 $\overline {G}$
.
$\overline {G}$
.
We remark that the
![]() $n/\log n$
blowup size in Theorems 1.2–1.4 are optimal up to a constant factor by a construction in [Reference Fox13].
$n/\log n$
blowup size in Theorems 1.2–1.4 are optimal up to a constant factor by a construction in [Reference Fox13].
To prove Theorem 1.4, we reduce the problem of upper bounding
![]() $g(k)$
to a Ramsey problem (see Definition 3.1). The lower bound construction is geometric and utilises concentration of measure and isodiametric inequality on high dimensional spheres, motivated by the Bollobás–Erdős graph in Ramsey–Turán theory [Reference Balogh and Lenz3, Reference Bollobás and Erdős4, Reference Fox, Loh and Zhao14, Reference Liu, Reiher, Sharifzadeh and Staden24]. It is interesting to see such a connection between these two seemingly unrelated problems.
$g(k)$
to a Ramsey problem (see Definition 3.1). The lower bound construction is geometric and utilises concentration of measure and isodiametric inequality on high dimensional spheres, motivated by the Bollobás–Erdős graph in Ramsey–Turán theory [Reference Balogh and Lenz3, Reference Bollobás and Erdős4, Reference Fox, Loh and Zhao14, Reference Liu, Reiher, Sharifzadeh and Staden24]. It is interesting to see such a connection between these two seemingly unrelated problems.
1.2.2. Graphs on posets
Given a partially ordered set
![]() $(P,\prec )$
, its (in)comparability graph is a graph with vertex set
$(P,\prec )$
, its (in)comparability graph is a graph with vertex set
![]() $P$
in which two vertices form an edge if and only if the corresponding elements are (in)comparable in
$P$
in which two vertices form an edge if and only if the corresponding elements are (in)comparable in
![]() $P$
. Fox, Pach and Tóth [Reference Fox, Pach and Tóth17] proved the following result on existence of large complete bipartite graph in incomparability graphs with positive edge density.
$P$
. Fox, Pach and Tóth [Reference Fox, Pach and Tóth17] proved the following result on existence of large complete bipartite graph in incomparability graphs with positive edge density.
Theorem 1.5 (Fox–Pach–Tóth [Reference Fox, Pach and Tóth17]). Let
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $G$
be an
$G$
be an
![]() $n$
-vertex incomparability graph with
$n$
-vertex incomparability graph with
![]() $\varrho _2(G)\gt \varepsilon$
. Then
$\varrho _2(G)\gt \varepsilon$
. Then
![]() $G$
contains a
$G$
contains a
![]() ${K_2}[{{cn} \over {\log n}}]$
, where
${K_2}[{{cn} \over {\log n}}]$
, where
![]() $c=c(\varepsilon )\gt 0$
.
$c=c(\varepsilon )\gt 0$
.
Later this result was generalised for
![]() $k\gt 2$
by Tomon [Reference Tomon33], who showed that if an incomparability graph
$k\gt 2$
by Tomon [Reference Tomon33], who showed that if an incomparability graph
![]() $G$
satisfies
$G$
satisfies
![]() ${\varrho _2}(G)\geqslant 1 - {1 \over {9(k - 1)}} + \varepsilon $
, then
${\varrho _2}(G)\geqslant 1 - {1 \over {9(k - 1)}} + \varepsilon $
, then
![]() $G$
contains a copy of
$G$
contains a copy of
![]() ${K_k}[{{cn} \over {{{(\log n)}^s}}}]$
, where
${K_k}[{{cn} \over {{{(\log n)}^s}}}]$
, where
![]() $c=c(k,\varepsilon )\gt 0$
and
$c=c(k,\varepsilon )\gt 0$
and
![]() $s=\lceil \log _{2}k\rceil$
. Tomon proposed the following conjecture.
$s=\lceil \log _{2}k\rceil$
. Tomon proposed the following conjecture.
Conjecture B (Tomon [Reference Tomon33]). Let
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $G$
be an
$G$
be an
![]() $n$
-vertex incomparability graph with
$n$
-vertex incomparability graph with
![]() ${\varrho _2}(G)\gt 1 - {1 \over {k - 1}} + \varepsilon $
. Then
${\varrho _2}(G)\gt 1 - {1 \over {k - 1}} + \varepsilon $
. Then
![]() $G$
contains a
$G$
contains a
![]() ${K_k}[{{cn} \over {{{(\log n)}^s}}}]$
, where
${K_k}[{{cn} \over {{{(\log n)}^s}}}]$
, where
![]() $c=c(\varepsilon ,k)\gt 0$
and
$c=c(\varepsilon ,k)\gt 0$
and
![]() $s=\lceil \log _{2}k\rceil$
.
$s=\lceil \log _{2}k\rceil$
.
Our next result resolves Conjecture B in a stronger form using the weaker clique density condition. The size of the blowup
![]() $n/\log n$
below is best possible up to a constant factor by [Reference Fox13].
$n/\log n$
below is best possible up to a constant factor by [Reference Fox13].
Theorem 1.6.
Let
![]() $c \in (0,{1 \over 2})$
,
$c \in (0,{1 \over 2})$
,
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $n$
be sufficiently large. If
$n$
be sufficiently large. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex incomparability graph with
$n$
-vertex incomparability graph with
![]() $\varrho _k(G)\geqslant c$
, then
$\varrho _k(G)\geqslant c$
, then
![]() $G$
contains a
$G$
contains a
![]() ${K_k}[{{{c^4}n} \over {{{10}^8}{k^2}\log n}}]$
.
${K_k}[{{{c^4}n} \over {{{10}^8}{k^2}\log n}}]$
.
To prove Theorem 1.6, we obtain a strong regularity type lemma for incomparability graphs not containing large blowups of
![]() $K_k$
. We prove that such graphs admit regular partitions where almost all pairs of clusters are homogeneous, that is, they form either complete or empty bipartite graphs. Such regularity type result is of independent interest. A similar type of partition lemma was recently obtained for intersection graphs of pseudosegments by Fox, Pach, and Suk [Reference Fox, Pach and Suk16].
$K_k$
. We prove that such graphs admit regular partitions where almost all pairs of clusters are homogeneous, that is, they form either complete or empty bipartite graphs. Such regularity type result is of independent interest. A similar type of partition lemma was recently obtained for intersection graphs of pseudosegments by Fox, Pach, and Suk [Reference Fox, Pach and Suk16].
Theorem 1.7.
Let
![]() $k \geqslant 2$
and
$k \geqslant 2$
and
![]() $0\lt \varepsilon \lt 1$
. Suppose
$0\lt \varepsilon \lt 1$
. Suppose
![]() $n$
is sufficiently large and set
$n$
is sufficiently large and set
![]() $q = {{{\varepsilon ^4}n} \over {{{10}^5}{k^2}\log n}}$
and
$q = {{{\varepsilon ^4}n} \over {{{10}^5}{k^2}\log n}}$
and
![]() $t = {{{\varepsilon ^7}n} \over {{{10}^{11}}{k^5}}}.$
Let
$t = {{{\varepsilon ^7}n} \over {{{10}^{11}}{k^5}}}.$
Let
![]() $G$
be an incomparability graph on
$G$
be an incomparability graph on
![]() $n$
vertices with no copy of
$n$
vertices with no copy of
![]() $K_k[q].$
Then, there exists a partition
$K_k[q].$
Then, there exists a partition
![]() $V(G) = V_0 \sqcup V_1 \sqcup \cdots \sqcup V_m$
such that
$V(G) = V_0 \sqcup V_1 \sqcup \cdots \sqcup V_m$
such that
![]() $|V_0| \leqslant \varepsilon n,$
$|V_0| \leqslant \varepsilon n,$
![]() $|V_1| = |V_2| = \dots = |V_m| = t$
and all but at most
$|V_1| = |V_2| = \dots = |V_m| = t$
and all but at most
![]() $\varepsilon m^2$
pairs
$\varepsilon m^2$
pairs
![]() $(V_i, V_j), 1 \leqslant i \lt j \leqslant m,$
are homogeneous.
$(V_i, V_j), 1 \leqslant i \lt j \leqslant m,$
are homogeneous.
Next, we consider unions of comparability graphs. Given partial orders
![]() $\prec _{1},\ldots ,\prec _{r}$
on the same set
$\prec _{1},\ldots ,\prec _{r}$
on the same set
![]() $P$
, the corresponding
$P$
, the corresponding
![]() $r$
-comparability graph
$r$
-comparability graph
![]() $G=G({\prec}_{1},\ldots ,\prec _{r})$
is the graph whose vertex set is
$G=G({\prec}_{1},\ldots ,\prec _{r})$
is the graph whose vertex set is
![]() $P$
and two elements
$P$
and two elements
![]() $a,b\in P$
are adjacent if and only if
$a,b\in P$
are adjacent if and only if
![]() $a\prec _{i} b$
or
$a\prec _{i} b$
or
![]() $b \prec _i a$
holds for some
$b \prec _i a$
holds for some
![]() $1\leqslant i\leqslant r$
. In other words,
$1\leqslant i\leqslant r$
. In other words,
![]() $G$
is the union of
$G$
is the union of
![]() $r$
comparability graphs
$r$
comparability graphs
![]() $G=\bigcup _{i\in [r]}G({\prec}_{i})$
.
$G=\bigcup _{i\in [r]}G({\prec}_{i})$
.
Theorem 1.8.
Let
![]() $r,h\in \mathbb{N}$
with
$r,h\in \mathbb{N}$
with
![]() $h\geqslant 2$
,
$h\geqslant 2$
,
![]() $k=(2h-2)^{r}+1$
and
$k=(2h-2)^{r}+1$
and
![]() $\varepsilon \gt 0$
. Let
$\varepsilon \gt 0$
. Let
![]() $G=\bigcup _{i\in [r]}G({\prec}_{i})$
be an
$G=\bigcup _{i\in [r]}G({\prec}_{i})$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $r$
-comparability graph. If
$r$
-comparability graph. If
![]() $\varrho _k(G)\geqslant \varepsilon$
, then some
$\varrho _k(G)\geqslant \varepsilon$
, then some
![]() $G({\prec}_{i})$
,
$G({\prec}_{i})$
,
![]() $i\in [r]$
, contains a copy of
$i\in [r]$
, contains a copy of
![]() ${K_h}[{{\varepsilon n} \over r}]$
.
${K_h}[{{\varepsilon n} \over r}]$
.
This strengthens a result of Tomon [Reference Tomon33] which requires the stronger edge density condition
![]() ${\varrho _2}(G)\geqslant 1 - {1 \over {{{(2h - 2)}^r}}} + \varepsilon $
. The constant
${\varrho _2}(G)\geqslant 1 - {1 \over {{{(2h - 2)}^r}}} + \varepsilon $
. The constant
![]() $k=(2h-2)^r+1$
in Theorem 1.8 is best possible by [Reference Tomon33, Theorem 4(i)].
$k=(2h-2)^r+1$
in Theorem 1.8 is best possible by [Reference Tomon33, Theorem 4(i)].
Both Theorems 1.6 and 1.8 also fall in the theme of ‘replacing edge density by clique density’.
1.2.3. Hereditary graphs and
 $B_k$
property
$B_k$
property
Next we consider Question A for hereditary families. A family of graphs
![]() $\mathcal{G}$
is hereditary, if for any graph
$\mathcal{G}$
is hereditary, if for any graph
![]() $G\in \mathcal{G}$
and any induced subgraph
$G\in \mathcal{G}$
and any induced subgraph
![]() $G'$
of
$G'$
of
![]() $G$
,
$G$
,
![]() $G'\in \mathcal{G}$
. We introduce the following notion of the
$G'\in \mathcal{G}$
. We introduce the following notion of the
![]() $B_{k}$
property. A notion similar to the
$B_{k}$
property. A notion similar to the
![]() $B_{2}$
property has recently been introduced by Fox, Pach, and Suk [Reference Fox, Pach and Suk16].
$B_{2}$
property has recently been introduced by Fox, Pach, and Suk [Reference Fox, Pach and Suk16].
Definition.
Let
![]() $k\geqslant 2$
. A graph class
$k\geqslant 2$
. A graph class
![]() $\mathcal{G}$
has the
$\mathcal{G}$
has the
![]() $B_k$
property with function
$B_k$
property with function
![]() $f\,:\, \mathbb{R}^+\rightarrow \mathbb{R}^+$
if the following holds. For any
$f\,:\, \mathbb{R}^+\rightarrow \mathbb{R}^+$
if the following holds. For any
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $n$
-vertex
$n$
-vertex
![]() $G\in \mathcal{G}$
, if
$G\in \mathcal{G}$
, if
![]() $\varrho _k(G)\gt \varepsilon$
, then
$\varrho _k(G)\gt \varepsilon$
, then
![]() $G$
contains a
$G$
contains a
![]() $K_{k}[f(\varepsilon )n]$
.
$K_{k}[f(\varepsilon )n]$
.
Our next result states that the
![]() $B_2$
property implies the
$B_2$
property implies the
![]() $B_k$
property for all
$B_k$
property for all
![]() $k \geqslant 2.$
$k \geqslant 2.$
Theorem 1.9.
If a hereditary family of graphs has the
![]() $B_2$
property, then it also has the
$B_2$
property, then it also has the
![]() $B_k$
property for all
$B_k$
property for all
![]() $k \geqslant 2$
(possibly with a different function
$k \geqslant 2$
(possibly with a different function
![]() $f$
).
$f$
).
Several classes of graphs are known to have the
![]() $B_{2}$
property. For instance, Fox, Pach, and Tóth [Reference Fox, Pach and Tóth17] proved it for intersection graphs of planar convex sets as well as for incomparability graphs of posets with bounded dimension. Although the proof in [Reference Fox, Pach and Tóth17] is quite combinatorial, it is not clear how to adapt it to show e.g., that if the intersection graph of planar convex sets has positive triangle density, then it has a linear-size complete tripartite graph, that is, such graphs have the
$B_{2}$
property. For instance, Fox, Pach, and Tóth [Reference Fox, Pach and Tóth17] proved it for intersection graphs of planar convex sets as well as for incomparability graphs of posets with bounded dimension. Although the proof in [Reference Fox, Pach and Tóth17] is quite combinatorial, it is not clear how to adapt it to show e.g., that if the intersection graph of planar convex sets has positive triangle density, then it has a linear-size complete tripartite graph, that is, such graphs have the
![]() $B_3$
property. Our Theorem 1.9 circumvents ad-hoc family-specific arguments and show that all families with the
$B_3$
property. Our Theorem 1.9 circumvents ad-hoc family-specific arguments and show that all families with the
![]() $B_2$
property also have the
$B_2$
property also have the
![]() $B_k$
property.
$B_k$
property.
Here we present another hereditary class with the
![]() $B_{2}$
property. The Vapnik-Chervonenkis dimension, or VC-dimension for short, of a graph and, more generally, a set system, is a fundamental parameter that measures its combinatorial complexity. We defer its formal definition to Section 6.
$B_{2}$
property. The Vapnik-Chervonenkis dimension, or VC-dimension for short, of a graph and, more generally, a set system, is a fundamental parameter that measures its combinatorial complexity. We defer its formal definition to Section 6.
Theorem 1.10.
The family of graphs with VC-dimension
![]() $d$
has the
$d$
has the
![]() $B_2$
property if and only if
$B_2$
property if and only if
![]() $d=1$
.
$d=1$
.
Structure of the paper. In Section 2, we provide some useful tools and auxiliary results. The proof of Theorem 1.4 is given in Sections 3 and 4. We prove Theorems 1.6 to 1.8 in Section 5, and Theorems 1.9 and 1.10 in Section 6. Concluding remarks are given in Section 7.
2. Tools and some auxiliary results
All undirected graphs in this paper are simple. For the sake of clarity of presentation, we omit floor and ceiling signs whenever they are not essential.
Let
![]() $G$
be a graph. We will denote the set of vertices of
$G$
be a graph. We will denote the set of vertices of
![]() $G$
by
$G$
by
![]() $V(G)$
and the set of edges by
$V(G)$
and the set of edges by
![]() $E(G)$
, and define
$E(G)$
, and define
![]() $|G| \,:\!=\, |V(G)|$
and
$|G| \,:\!=\, |V(G)|$
and
![]() $e(G)\,:\!=\,|E(G)|$
. For any vertex
$e(G)\,:\!=\,|E(G)|$
. For any vertex
![]() $v\in G$
, we define
$v\in G$
, we define
![]() $N(v)$
as the neighbour of
$N(v)$
as the neighbour of
![]() $G$
. We say a graph
$G$
. We say a graph
![]() $G$
is
$G$
is
![]() $(\alpha ,\beta )$
-dense if for every
$(\alpha ,\beta )$
-dense if for every
![]() $S \subseteq V(G)$
with
$S \subseteq V(G)$
with
![]() $|S| \geqslant \alpha |V(G)|$
,
$|S| \geqslant \alpha |V(G)|$
,
![]() $e(G[S]) \geqslant \beta \binom{|S|}{2}$
holds.
$e(G[S]) \geqslant \beta \binom{|S|}{2}$
holds.
For a graph
![]() $G$
, let
$G$
, let
![]() $X$
,
$X$
,
![]() $Y$
be disjoint subsets of
$Y$
be disjoint subsets of
![]() $V(G)$
, and
$V(G)$
, and
![]() $e(X,Y)$
be the number of edges between
$e(X,Y)$
be the number of edges between
![]() $X$
and
$X$
and
![]() $Y$
. We define the density of the pair
$Y$
. We define the density of the pair
![]() $(X,Y)$
as
$(X,Y)$
as
![]() $d(X,Y)\,:\!=\, {{e(X,Y)} \over {|X| \cdot |Y|}}$
. A pair of vertex sets
$d(X,Y)\,:\!=\, {{e(X,Y)} \over {|X| \cdot |Y|}}$
. A pair of vertex sets
![]() $X$
and
$X$
and
![]() $Y$
is said to be
$Y$
is said to be
![]() $\varepsilon$
-regular, if for all subsets
$\varepsilon$
-regular, if for all subsets
![]() $A\subseteq X$
,
$A\subseteq X$
,
![]() $B\subseteq Y$
satisfying
$B\subseteq Y$
satisfying
![]() $|A|\geqslant \varepsilon |X|$
,
$|A|\geqslant \varepsilon |X|$
,
![]() $|B|\geqslant \varepsilon |Y|$
, we have
$|B|\geqslant \varepsilon |Y|$
, we have
A partition of
![]() $V$
into
$V$
into
![]() $k+1$
sets
$k+1$
sets
![]() $(V_0,V_{1},\ldots ,V_{k})$
is called an
$(V_0,V_{1},\ldots ,V_{k})$
is called an
![]() $\varepsilon$
-regular partition, if
$\varepsilon$
-regular partition, if
-
•
 $|V_0|\lt \varepsilon n$
and for all
$|V_0|\lt \varepsilon n$
and for all
 $1\leqslant i\lt j\leqslant k$
we have
$1\leqslant i\lt j\leqslant k$
we have
 $|V_{i}|=|V_{j}|$
, and
$|V_{i}|=|V_{j}|$
, and -
• all except
 $\varepsilon k^{2}$
of the pairs
$\varepsilon k^{2}$
of the pairs
 $V_{i},V_{j}$
,
$V_{i},V_{j}$
,
 $1\leqslant i\lt j\leqslant k$
, are
$1\leqslant i\lt j\leqslant k$
, are
 $\varepsilon$
-regular.
$\varepsilon$
-regular.
The famous Szemerédi’s regularity lemma [Reference Szemerédi31] can be stated as follows.
Lemma 2.1 (Szemerédi regularity lemma, [Reference Szemerédi31]). For all
![]() $m,\varepsilon \gt 0$
, there exists an integer
$m,\varepsilon \gt 0$
, there exists an integer
![]() $M$
such that the following holds. If a graph
$M$
such that the following holds. If a graph
![]() $G$
has
$G$
has
![]() $n\geqslant M$
vertices, there exists an integer
$n\geqslant M$
vertices, there exists an integer
![]() $K$
satisfying
$K$
satisfying
![]() $m \leqslant K \leqslant M$
, and an
$m \leqslant K \leqslant M$
, and an
![]() $\varepsilon$
-regular partition
$\varepsilon$
-regular partition
![]() $\mathcal{P}$
of
$\mathcal{P}$
of
![]() $V(G)$
with
$V(G)$
with
![]() $K+1$
parts.
$K+1$
parts.
We will also use the following simple lemma on the regular pairs.
Lemma 2.2 (Slicing lemma, [Reference Komlós and Simonovits22]). Let
![]() $(A, B)$
be an
$(A, B)$
be an
![]() $\varepsilon$
-regular pair with density
$\varepsilon$
-regular pair with density
![]() $d,$
and, for
$d,$
and, for
![]() $\alpha \gt \varepsilon ,$
let
$\alpha \gt \varepsilon ,$
let
![]() $A' \subseteq A$
and
$A' \subseteq A$
and
![]() $B' \subseteq B$
be subsets with
$B' \subseteq B$
be subsets with
![]() $|A'| \geqslant \alpha |A|, |B'| \geqslant \alpha |B|$
. Then
$|A'| \geqslant \alpha |A|, |B'| \geqslant \alpha |B|$
. Then
![]() $(A', B')$
is an
$(A', B')$
is an
![]() $\varepsilon '$
-regular pair with
$\varepsilon '$
-regular pair with
![]() $\varepsilon ' = \max \{\varepsilon / \alpha , 2 \varepsilon \}$
. Moreover, let
$\varepsilon ' = \max \{\varepsilon / \alpha , 2 \varepsilon \}$
. Moreover, let
![]() $d'$
be the edge density of
$d'$
be the edge density of
![]() $(A',B')$
, we have
$(A',B')$
, we have
![]() $|d^{\prime} - d| \lt \varepsilon$
.
$|d^{\prime} - d| \lt \varepsilon$
.
We will use multiple times the following simple consequence of the regularity lemma.
Lemma 2.3.
For every integer
![]() $k \geqslant 2,$
and any reals
$k \geqslant 2,$
and any reals
![]() $\eta , \varepsilon \gt 0,$
there is a real
$\eta , \varepsilon \gt 0,$
there is a real
![]() $\gamma \gt 0$
such that the following holds. Let
$\gamma \gt 0$
such that the following holds. Let
![]() $G = G_\lt$
be an ordered graph on
$G = G_\lt$
be an ordered graph on
![]() $n$
vertices with at least
$n$
vertices with at least
![]() $\eta n^k$
copies of
$\eta n^k$
copies of
![]() $K_k.$
Then, there are sets
$K_k.$
Then, there are sets
![]() $A_1, \dots , A_k \subseteq V(G)$
with
$A_1, \dots , A_k \subseteq V(G)$
with
![]() $A_1 \lt A_2 \lt \dots \lt A_k$
such that
$A_1 \lt A_2 \lt \dots \lt A_k$
such that
![]() $|A_i| \geqslant \gamma n$
for all
$|A_i| \geqslant \gamma n$
for all
![]() $i \in [k]$
and the pair
$i \in [k]$
and the pair
![]() $(A_i, A_j)$
is
$(A_i, A_j)$
is
![]() $\varepsilon$
-regular in
$\varepsilon$
-regular in
![]() $G$
with density at least
$G$
with density at least
![]() ${\eta \over 2}$
for all
${\eta \over 2}$
for all
![]() $1 \leqslant i \lt j \leqslant k.$
$1 \leqslant i \lt j \leqslant k.$
Proof. Clearly we may assume that
![]() ${1 \over n} \ll \varepsilon \ll \eta \ll {1 \over k}$
. Let
${1 \over n} \ll \varepsilon \ll \eta \ll {1 \over k}$
. Let
![]() $\varepsilon ' = {\varepsilon \over k}$
and
$\varepsilon ' = {\varepsilon \over k}$
and
![]() $m = {1 \over {\varepsilon '}}$
. We apply Lemma 2.1 to
$m = {1 \over {\varepsilon '}}$
. We apply Lemma 2.1 to
![]() $G$
with parameters
$G$
with parameters
![]() $\varepsilon ', m$
to obtain an
$\varepsilon ', m$
to obtain an
![]() $\varepsilon '$
-regular partition
$\varepsilon '$
-regular partition
![]() $V_0, \dots , V_K.$
Note that there are at most
$V_0, \dots , V_K.$
Note that there are at most
![]() $|V_0| n^{k-1} \lt \varepsilon n^k$
$|V_0| n^{k-1} \lt \varepsilon n^k$
![]() $k$
-cliques in
$k$
-cliques in
![]() $G$
touching the set
$G$
touching the set
![]() $V_0.$
Additionally, there are at most
$V_0.$
Additionally, there are at most
![]() $\varepsilon K^2 |V_1|^2 \cdot n^{k-2} \leqslant \varepsilon n^k$
$\varepsilon K^2 |V_1|^2 \cdot n^{k-2} \leqslant \varepsilon n^k$
![]() $k$
-cliques with one of the edges across an irregular pair. Finally, there are at most
$k$
-cliques with one of the edges across an irregular pair. Finally, there are at most
![]() ${K^2}|{V_1}{|^2} \cdot {{2\eta } \over 3} \cdot {n^{k - 2}}\leqslant {{2\eta } \over 3} \cdot {n^k}$
${K^2}|{V_1}{|^2} \cdot {{2\eta } \over 3} \cdot {n^{k - 2}}\leqslant {{2\eta } \over 3} \cdot {n^k}$
![]() $k$
-cliques with one of the edges across pair with density at most
$k$
-cliques with one of the edges across pair with density at most
![]() ${{2\eta } \over 3}$
. Hence, there exist
${{2\eta } \over 3}$
. Hence, there exist
![]() $k$
sets, without loss of generality the sets
$k$
sets, without loss of generality the sets
![]() $V_1, \dots , V_k$
, such that each of the pairs
$V_1, \dots , V_k$
, such that each of the pairs
![]() $(V_i, V_j)$
is
$(V_i, V_j)$
is
![]() $\varepsilon$
-regular with density at least
$\varepsilon$
-regular with density at least
![]() ${{2\eta } \over 3}$
.
${{2\eta } \over 3}$
.
Denote
![]() $n_0 = |V_1| = \dots = |V_k|.$
We shall find the desired subsets
$n_0 = |V_1| = \dots = |V_k|.$
We shall find the desired subsets
![]() $A_1, \dots , A_k$
with
$A_1, \dots , A_k$
with
![]() $A_{i}\subseteq V_{i}$
for
$A_{i}\subseteq V_{i}$
for
![]() $i=1,2\ldots ,k$
. For a vertex
$i=1,2\ldots ,k$
. For a vertex
![]() $x \in V(G),$
let
$x \in V(G),$
let
![]() $V_{\leqslant x} = \{ y \in V(G), \, \vert \, y \leqslant x\}$
.
$V_{\leqslant x} = \{ y \in V(G), \, \vert \, y \leqslant x\}$
.
For
![]() $i \in [k],$
set
$i \in [k],$
set
![]() $U^1_i = V_i.$
Then, in steps
$U^1_i = V_i.$
Then, in steps
![]() $t = 1, \dots , k,$
we proceed as follows. Let
$t = 1, \dots , k,$
we proceed as follows. Let
![]() $x$
be the minimum vertex in
$x$
be the minimum vertex in
![]() $V(G)$
such that for some
$V(G)$
such that for some
![]() $i, t \leqslant i \leqslant k,$
we have
$i, t \leqslant i \leqslant k,$
we have
![]() $|U_i^t \cap {V_{\leqslant x}}| = {{{n_0}} \over k}$
. Without loss of generality, we may assume that
$|U_i^t \cap {V_{\leqslant x}}| = {{{n_0}} \over k}$
. Without loss of generality, we may assume that
![]() $i = t.$
Then, set
$i = t.$
Then, set
![]() $A_i = U_i^t \cap V_{\leqslant x}$
and for
$A_i = U_i^t \cap V_{\leqslant x}$
and for
![]() $j, i+1 \leqslant j \leqslant k,$
define
$j, i+1 \leqslant j \leqslant k,$
define
![]() $U^{t+1}_j = U^t_j {\setminus} V_{\leqslant x}.$
Observe that by definition of
$U^{t+1}_j = U^t_j {\setminus} V_{\leqslant x}.$
Observe that by definition of
![]() $x$
, we have
$x$
, we have
![]() $|U_j^{t + 1}|\geqslant |U_j^t| - {{{n_0}} \over k}$
. It is easy to see that the described procedure produces sets
$|U_j^{t + 1}|\geqslant |U_j^t| - {{{n_0}} \over k}$
. It is easy to see that the described procedure produces sets
![]() $A_1, \dots , A_k$
with
$A_1, \dots , A_k$
with
![]() ${A_1}\lt {A_2}\lt \ldots \lt {A_k},|{A_i}| = {{{n_0}} \over k}$
for all
${A_1}\lt {A_2}\lt \ldots \lt {A_k},|{A_i}| = {{{n_0}} \over k}$
for all
![]() $i \in [k]$
and each of
$i \in [k]$
and each of
![]() $A_i$
is a subset of a distinct set among
$A_i$
is a subset of a distinct set among
![]() $V_1, \dots , V_k.$
Finally, by Lemma 2.2, it follows that each of the pairs
$V_1, \dots , V_k.$
Finally, by Lemma 2.2, it follows that each of the pairs
![]() $(A_i, A_j)$
is
$(A_i, A_j)$
is
![]() $\varepsilon$
-regular with density at least
$\varepsilon$
-regular with density at least
![]() ${{2\eta } \over 3} - \varepsilon '\gt {\eta \over 2}$
, as needed.
${{2\eta } \over 3} - \varepsilon '\gt {\eta \over 2}$
, as needed.
Let
![]() $0\lt \gamma \lt 1$
be a real number, we say a pair of vertex sets
$0\lt \gamma \lt 1$
be a real number, we say a pair of vertex sets
![]() $(V_{1},V_{2})$
of
$(V_{1},V_{2})$
of
![]() $G$
is
$G$
is
![]() $\gamma$
-homogeneous if the density
$\gamma$
-homogeneous if the density
![]() $d(V_1,V_2)$
is either less than
$d(V_1,V_2)$
is either less than
![]() $\gamma$
or larger than
$\gamma$
or larger than
![]() $1-\gamma$
, where in the former case, we call
$1-\gamma$
, where in the former case, we call
![]() $(V_1,V_2)$
$(V_1,V_2)$
![]() $\gamma$
-sparse, and in the latter case, we call
$\gamma$
-sparse, and in the latter case, we call
![]() $(V_1,V_2)$
$(V_1,V_2)$
![]() $\gamma$
-dense. We call the pair
$\gamma$
-dense. We call the pair
![]() $(V_1, V_2)$
homogeneous if
$(V_1, V_2)$
homogeneous if
![]() $G[V_1, V_2]$
is empty or complete. A partition of
$G[V_1, V_2]$
is empty or complete. A partition of
![]() $V(G)$
is called equitable if every two parts differ in size by at most one.
$V(G)$
is called equitable if every two parts differ in size by at most one.
We will use the following recent result of Fox and Pham [Reference Fox and Pham18].
Lemma 2.4 (Fox–Pham [Reference Fox and Pham18]). Let
![]() $\ell \geqslant 2$
and
$\ell \geqslant 2$
and
![]() $n\geqslant (100\ell )^5$
. Every poset on
$n\geqslant (100\ell )^5$
. Every poset on
![]() $n$
elements contains
$n$
elements contains
![]() $\ell$
disjoint sets
$\ell$
disjoint sets
![]() $A_1,\ldots , A_\ell$
such that
$A_1,\ldots , A_\ell$
such that
-
• either
 $A_1\succ A_2\succ \cdots \succ A_\ell$
and
$A_1\succ A_2\succ \cdots \succ A_\ell$
and
 $|{A_i}| = {n \over {{{10}^4}{\ell ^5}}}$
for
$|{A_i}| = {n \over {{{10}^4}{\ell ^5}}}$
for
 $1\leqslant i\leqslant \ell ,$
or
$1\leqslant i\leqslant \ell ,$
or
-
•
 $A_i$
are pairwise incomparable and
$A_i$
are pairwise incomparable and
 $|{A_i}| = {n \over {40{\ell ^2}\log n}}$
for
$|{A_i}| = {n \over {40{\ell ^2}\log n}}$
for
 $1\leqslant i\leqslant \ell$
.
$1\leqslant i\leqslant \ell$
.
For a given
![]() $h$
-dimensional unit sphere
$h$
-dimensional unit sphere
![]() $\mathbb{S}^h$
, we write
$\mathbb{S}^h$
, we write
![]() $\lambda$
for the Lebesgue measure, which is normalised such that the unit sphere has Lebesgue measure
$\lambda$
for the Lebesgue measure, which is normalised such that the unit sphere has Lebesgue measure
![]() $1$
. For two subsets
$1$
. For two subsets
![]() $A,B$
of a unit sphere, we define the Euclidean distance between them to be
$A,B$
of a unit sphere, we define the Euclidean distance between them to be
![]() $d_{\max }(A,B)\,:\!=\,\sup \{|\boldsymbol{a}-\boldsymbol{b}|\,:\,\boldsymbol{a}\in A,\boldsymbol{b}\in B\}$
. We also define the diameter of
$d_{\max }(A,B)\,:\!=\,\sup \{|\boldsymbol{a}-\boldsymbol{b}|\,:\,\boldsymbol{a}\in A,\boldsymbol{b}\in B\}$
. We also define the diameter of
![]() $A$
as
$A$
as
![]() $\text {diam}(A)\,:\!=\,d_{\max }(A,A)$
.
$\text {diam}(A)\,:\!=\,d_{\max }(A,A)$
.
We will take advantage of the following lemma in [Reference Liu, Reiher, Sharifzadeh and Staden24].
Lemma 2.5 [Reference Liu, Reiher, Sharifzadeh and Staden24]. Let
![]() $\mu \in (0,1)$
and
$\mu \in (0,1)$
and
![]() $A,B\subseteq \mathbb{S}^{k-1}$
with
$A,B\subseteq \mathbb{S}^{k-1}$
with
![]() $\lambda (A),\lambda (B)\gt {e^{ - {{k\mu } \over 2}}}$
, then
$\lambda (A),\lambda (B)\gt {e^{ - {{k\mu } \over 2}}}$
, then
![]() $d_{\max }(A,B)\geqslant 2-\mu$
.
$d_{\max }(A,B)\geqslant 2-\mu$
.
A spherical cap is the smaller intersection of the unit sphere with a half-space. Given a spherical cap
![]() $C$
bounded by some hyperplane
$C$
bounded by some hyperplane
![]() $H$
, we call the point in
$H$
, we call the point in
![]() $C$
with maximum Euclidean distance to
$C$
with maximum Euclidean distance to
![]() $H$
the centre of the spherical cap. The distance from the centre to
$H$
the centre of the spherical cap. The distance from the centre to
![]() $H$
is the height of the spherical cap and the diameter of
$H$
is the height of the spherical cap and the diameter of
![]() $C$
is the diameter of the intersection of
$C$
is the diameter of the intersection of
![]() $C$
and
$C$
and
![]() $H$
.
$H$
.
We will use the following lower and upper bounds on the measure of spherical caps.
Lemma 2.6 [Reference Liu, Reiher, Sharifzadeh and Staden24]. For all
![]() $\delta \gt 0$
and integers
$\delta \gt 0$
and integers
![]() $k\geqslant 3$
, let
$k\geqslant 3$
, let
![]() $B\subseteq \mathbb{S}^{k-1}$
be the spherical cap consisting of all points with distance at most
$B\subseteq \mathbb{S}^{k-1}$
be the spherical cap consisting of all points with distance at most
![]() $\sqrt {2}-\delta /\sqrt {k}$
from a fixed point in
$\sqrt {2}-\delta /\sqrt {k}$
from a fixed point in
![]() $\mathbb{S}^{k-1}$
. Then
$\mathbb{S}^{k-1}$
. Then
![]() $\lambda (B)\geqslant 1/2-\sqrt {2}\delta$
.
$\lambda (B)\geqslant 1/2-\sqrt {2}\delta$
.
Lemma 2.7 [Reference Tkocz32]. Let
![]() $\alpha \in [0,1)$
and
$\alpha \in [0,1)$
and
![]() $C\subseteq \mathbb{S}^{k-1}$
be a spherical cap with height
$C\subseteq \mathbb{S}^{k-1}$
be a spherical cap with height
![]() $1-\alpha$
. Then
$1-\alpha$
. Then
![]() $\lambda (C)\leqslant e^{-k\alpha ^2/2}$
.
$\lambda (C)\leqslant e^{-k\alpha ^2/2}$
.
Recall that a spherical cap with height
![]() $1-\alpha$
has diameter
$1-\alpha$
has diameter
![]() $2\sqrt {1-\alpha ^2}$
.
$2\sqrt {1-\alpha ^2}$
.
The following folklore result partitions the sphere into small pieces of equal measure (see e.g., [Reference Feige and Schechtman12]).
Lemma 2.8.
There exists
![]() $C\gt 0$
such that the following holds. Let
$C\gt 0$
such that the following holds. Let
![]() $0\lt \delta \lt 1$
and
$0\lt \delta \lt 1$
and
![]() $n\geqslant (C/\delta )^k$
. Then
$n\geqslant (C/\delta )^k$
. Then
![]() $\mathbb{S}^{k-1}$
can be partitioned into
$\mathbb{S}^{k-1}$
can be partitioned into
![]() $n$
pieces of equal measure, each of diameter at most
$n$
pieces of equal measure, each of diameter at most
![]() $\delta$
.
$\delta$
.
We also need the following geometric property, which plays a key role in the original Bollobás–Erdős graph [Reference Bollobás and Erdős4].
Theorem 2.9.
For all
![]() $k\in \mathbb{N}$
and all
$k\in \mathbb{N}$
and all
![]() $0\lt \mu \lt {1 \over 4}$
, there do not exist four points
$0\lt \mu \lt {1 \over 4}$
, there do not exist four points
![]() $p_{1},p_{2},q_{1},q_{2}\in \mathbb{S}^{k}$
such that
$p_{1},p_{2},q_{1},q_{2}\in \mathbb{S}^{k}$
such that
![]() $|p_{1}-p_{2}|\geqslant 2-\mu$
,
$|p_{1}-p_{2}|\geqslant 2-\mu$
,
![]() $|q_{1}-q_{2}|\geqslant 2-\mu$
and
$|q_{1}-q_{2}|\geqslant 2-\mu$
and
![]() $|p_{i}-q_{j}|\leqslant \sqrt {2}-\mu$
for all
$|p_{i}-q_{j}|\leqslant \sqrt {2}-\mu$
for all
![]() $i,j\in [2]$
.
$i,j\in [2]$
.
3. Upper bound for Theorem 1.4
In this section we prove the upper bound on
![]() $g(k)$
in Theorem 1.4. To achieve this, we first introduce a framework and a Ramsey variant based on some auxiliary directed graphs.
$g(k)$
in Theorem 1.4. To achieve this, we first introduce a framework and a Ramsey variant based on some auxiliary directed graphs.
3.1. A Ramsey problem
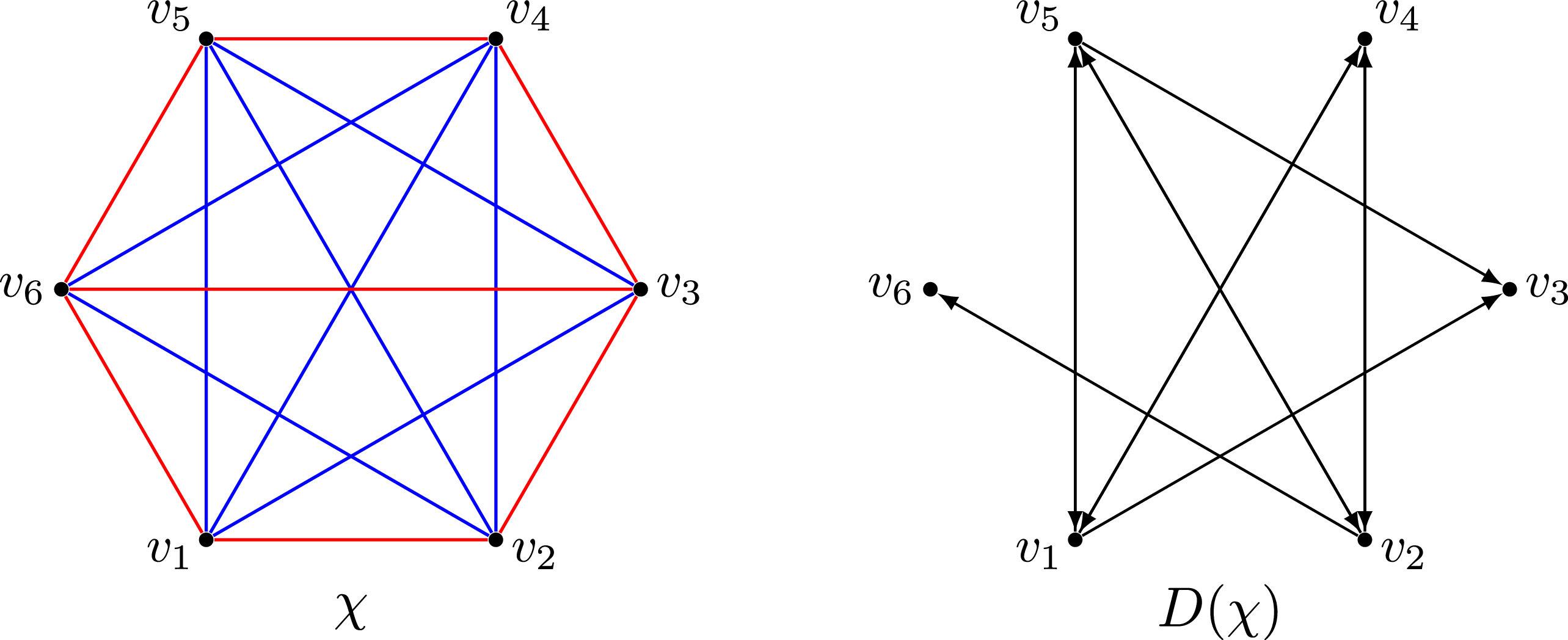
Definition 3.1.
Let
![]() $\chi$
be a red-blue edge-colouring of the ordered clique with vertices
$\chi$
be a red-blue edge-colouring of the ordered clique with vertices
![]() $v_1 \lt v_2 \lt \dots \lt v_k.$
Its dependency digraph
$v_1 \lt v_2 \lt \dots \lt v_k.$
Its dependency digraph
![]() $D = D(\chi )$
is defined on the vertex set
$D = D(\chi )$
is defined on the vertex set
![]() $\{v_1, \dots , v_k\}$
as follows. For every
$\{v_1, \dots , v_k\}$
as follows. For every
![]() $i \in [k-1]$
and
$i \in [k-1]$
and
![]() $j \in [k] {\setminus} \{i, i+1\},$
if
$j \in [k] {\setminus} \{i, i+1\},$
if
![]() $\chi (v_iv_{i+1}) = \mathrm{red}$
and
$\chi (v_iv_{i+1}) = \mathrm{red}$
and
![]() $\chi (v_iv_j) = \chi (v_{i+1}v_j) = \mathrm{blue}$
, then
$\chi (v_iv_j) = \chi (v_{i+1}v_j) = \mathrm{blue}$
, then
![]() $D$
contains the directed edges
$D$
contains the directed edges
![]() $(v_j, v_i)$
and
$(v_j, v_i)$
and
![]() $(v_j, v_{i+1}).$
We say that
$(v_j, v_{i+1}).$
We say that
![]() $\chi$
is admissible if
$\chi$
is admissible if
![]() $D(\chi )$
is acyclic.
$D(\chi )$
is acyclic.
For
![]() $k \geqslant 1,$
let
$k \geqslant 1,$
let
![]() $f(k)$
denote the minimum integer
$f(k)$
denote the minimum integer
![]() $N$
such that in any red-blue edge-colouring of the ordered clique on
$N$
such that in any red-blue edge-colouring of the ordered clique on
![]() $N$
vertices, there exist
$N$
vertices, there exist
![]() $k$
vertices such that the colouring induced on these
$k$
vertices such that the colouring induced on these
![]() $k$
vertices is admissible.
$k$
vertices is admissible.
Note that
![]() $D$
may contain bidirectional edges, which can be viewed as directed cycles of length two; see Fig. 1 for an example. To clarify, the induced colouring inherits the vertex ordering as well as the colours of the edges.
$D$
may contain bidirectional edges, which can be viewed as directed cycles of length two; see Fig. 1 for an example. To clarify, the induced colouring inherits the vertex ordering as well as the colours of the edges.

Figure 1. An example of dependency digraph.
The main result of this section is the following embedding result which relates the problem of upper bounding
![]() $g(k)$
to the Ramsey problem for
$g(k)$
to the Ramsey problem for
![]() $f(k)$
.
$f(k)$
.
Theorem 3.2.
For any integer
![]() $k \geqslant 1,$
and real
$k \geqslant 1,$
and real
![]() $\eta \gt 0,$
there exists
$\eta \gt 0,$
there exists
![]() $c \gt 0$
such that the following holds. Let
$c \gt 0$
such that the following holds. Let
![]() $G = G_\lt$
be an ordered graph with no induced monotone
$G = G_\lt$
be an ordered graph with no induced monotone
![]() $P_{2k}$
. If
$P_{2k}$
. If
![]() $\overline {G}$
contains at least
$\overline {G}$
contains at least
![]() $\eta n^{f(k)}$
copies of
$\eta n^{f(k)}$
copies of
![]() $K_{f(k)}$
, then
$K_{f(k)}$
, then
![]() $\overline {G}$
contains a
$\overline {G}$
contains a
![]() ${K_2}[{{cn} \over {\log n}}]$
. In other words,
${K_2}[{{cn} \over {\log n}}]$
. In other words,
Let us first derive that
![]() $g(3)=f(3)=3$
and
$g(3)=f(3)=3$
and
![]() $g(4)=f(4)=5$
, which imply Theorems 1.2 and 1.3. Recall that the optimal construction for
$g(4)=f(4)=5$
, which imply Theorems 1.2 and 1.3. Recall that the optimal construction for
![]() $\beta (5)=1/2$
infers that
$\beta (5)=1/2$
infers that
![]() $g(3)\gt 2$
and the construction in Theorem 1.4 shows that
$g(3)\gt 2$
and the construction in Theorem 1.4 shows that
![]() $g(4)\gt 4$
. Thus, by Theorem 3.2, it suffices to prove
$g(4)\gt 4$
. Thus, by Theorem 3.2, it suffices to prove
![]() $f(3)\leqslant 3$
and
$f(3)\leqslant 3$
and
![]() $f(4)\leqslant 5$
.
$f(4)\leqslant 5$
.
Corollary 3.3.
We have
![]() $f(3)\leqslant 3$
and
$f(3)\leqslant 3$
and
![]() $f(4)\leqslant 5$
. Consequently, for any
$f(4)\leqslant 5$
. Consequently, for any
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $n$
-vertex ordered graph
$n$
-vertex ordered graph
![]() $G$
with no induced monotone
$G$
with no induced monotone
![]() $P_{6}$
(or
$P_{6}$
(or
![]() $P_8$
resp.), if
$P_8$
resp.), if
![]() $\varrho _3(\overline {G})\gt \varepsilon$
(or
$\varrho _3(\overline {G})\gt \varepsilon$
(or
![]() $\varrho _5(\overline {G})\gt \varepsilon$
), then
$\varrho _5(\overline {G})\gt \varepsilon$
), then
![]() $\overline {G}$
contains a
$\overline {G}$
contains a
![]() ${K_2}[{{cn} \over {\log n}}]$
, where
${K_2}[{{cn} \over {\log n}}]$
, where
![]() $c=c(\varepsilon )\gt 0$
.
$c=c(\varepsilon )\gt 0$
.
Proof. To prove
![]() $f(3)\leqslant 3$
, we need to show that any red-blue colouring
$f(3)\leqslant 3$
, we need to show that any red-blue colouring
![]() $\chi$
of
$\chi$
of
![]() $\binom{[3]}{2}$
is admissible. We may assume that
$\binom{[3]}{2}$
is admissible. We may assume that
![]() $D(\chi )$
has at least one edge and thus by symmetry we may assume that
$D(\chi )$
has at least one edge and thus by symmetry we may assume that
![]() $\chi (1,2) = \mathrm{red}$
and
$\chi (1,2) = \mathrm{red}$
and
![]() $\chi (1, 3) = \chi (2, 3) = \mathrm{blue}$
. But then,
$\chi (1, 3) = \chi (2, 3) = \mathrm{blue}$
. But then,
![]() $E(D(\chi )) = \{ (3, 1), (3, 2) \},$
which is acyclic. Thus
$E(D(\chi )) = \{ (3, 1), (3, 2) \},$
which is acyclic. Thus
![]() $\chi$
is admissible as desired.
$\chi$
is admissible as desired.
To prove
![]() $f(4)\leqslant 5$
, let
$f(4)\leqslant 5$
, let
![]() $\chi$
be a red-blue colouring of
$\chi$
be a red-blue colouring of
![]() $\binom{[5]}{2}$
, we need to show that the induced colouring on some set of
$\binom{[5]}{2}$
, we need to show that the induced colouring on some set of
![]() $4$
vertices is admissible. Suppose
$4$
vertices is admissible. Suppose
![]() $D(\chi |_{1234})$
is not acyclic, for otherwise we are done. We claim that
$D(\chi |_{1234})$
is not acyclic, for otherwise we are done. We claim that
![]() $\chi (12)=\chi (34)=\mathrm{red}$
. To see this, suppose one of them is blue and by symmetry we may assume that
$\chi (12)=\chi (34)=\mathrm{red}$
. To see this, suppose one of them is blue and by symmetry we may assume that
![]() $\chi (34)=\mathrm{blue}$
. Now if
$\chi (34)=\mathrm{blue}$
. Now if
![]() $\chi (23)=\mathrm{red}$
, then
$\chi (23)=\mathrm{red}$
, then
![]() $D(\chi |_{1234})$
contains only edges from
$D(\chi |_{1234})$
contains only edges from
![]() $\{1,4\}$
to
$\{1,4\}$
to
![]() $\{2,3\}$
if
$\{2,3\}$
if
![]() $\chi (12)=\mathrm{blue}$
or only edges from
$\chi (12)=\mathrm{blue}$
or only edges from
![]() $\{4\}$
to
$\{4\}$
to
![]() $\{1,2,3\}$
if
$\{1,2,3\}$
if
![]() $\chi (12)=\mathrm{red}$
, both of which are acyclic. Thus we may assume
$\chi (12)=\mathrm{red}$
, both of which are acyclic. Thus we may assume
![]() $\chi (23)=\mathrm{blue}$
, and then
$\chi (23)=\mathrm{blue}$
, and then
![]() $D(\chi |_{1234})$
contains only edges from
$D(\chi |_{1234})$
contains only edges from
![]() $\{3,4\}$
to
$\{3,4\}$
to
![]() $\{1,2\}$
, which is acyclic.
$\{1,2\}$
, which is acyclic.
The above analysis shows that if none of
![]() $D(\chi |_{1234}), D(\chi |_{2345}), D(\chi |_{1345})$
is acyclic, then
$D(\chi |_{1234}), D(\chi |_{2345}), D(\chi |_{1345})$
is acyclic, then
![]() $\chi (12)=\chi (34)=\chi (23)=\chi (13)=\mathrm{red}$
and so
$\chi (12)=\chi (34)=\chi (23)=\chi (13)=\mathrm{red}$
and so
![]() $D(\chi |_{1234})$
contains only the edge from
$D(\chi |_{1234})$
contains only the edge from
![]() $\{4\}$
to
$\{4\}$
to
![]() $\{1,2\}$
, which is acyclic, a contradiction.
$\{1,2\}$
, which is acyclic, a contradiction.
We now prove an upper bound for the general case, which together with Theorem 3.2, implies the upper bound for
![]() $g(k)$
in Theorem 1.4.
$g(k)$
in Theorem 1.4.
Proposition 3.4.
We have
![]() $f(k) \leqslant {{{k^2} - k + 2} \over 2}$
.
$f(k) \leqslant {{{k^2} - k + 2} \over 2}$
.
Proof. Suppose for a contradiction that there exists a red-blue edge-colouring
![]() $\chi$
of the ordered clique on vertices
$\chi$
of the ordered clique on vertices
![]() $1,2, \cdots ,{{{k^2} - k + 2} \over 2}$
such that the colouring induced on any
$1,2, \cdots ,{{{k^2} - k + 2} \over 2}$
such that the colouring induced on any
![]() $k$
vertices is not admissible. If there exists
$k$
vertices is not admissible. If there exists
![]() $t$
vertices
$t$
vertices
![]() $i_1\lt \cdots \lt i_{t}$
such that
$i_1\lt \cdots \lt i_{t}$
such that
![]() $\chi (i_ri_{r+1})=\mathrm{blue}$
for any
$\chi (i_ri_{r+1})=\mathrm{blue}$
for any
![]() $1\leqslant r\leqslant t-1$
, we say these
$1\leqslant r\leqslant t-1$
, we say these
![]() $t$
vertices form a blue path with order
$t$
vertices form a blue path with order
![]() $t$
. For any vertices
$t$
. For any vertices
![]() $v_i$
, let
$v_i$
, let
![]() $\sigma (v_i)$
be the order of the longest blue path starting from
$\sigma (v_i)$
be the order of the longest blue path starting from
![]() $v_i$
. If there are no blue edge starting from
$v_i$
. If there are no blue edge starting from
![]() $v_i$
, set
$v_i$
, set
![]() $\sigma (v_i)=1$
. If there exists a blue path with order
$\sigma (v_i)=1$
. If there exists a blue path with order
![]() $k$
, then the colouring induced on these
$k$
, then the colouring induced on these
![]() $k$
vertices is admissible as
$k$
vertices is admissible as
![]() $D(\chi )$
is the empty graph, a contradiction. Let
$D(\chi )$
is the empty graph, a contradiction. Let
![]() $S_t=\{v_i|\sigma (v_i)=t\}$
for any
$S_t=\{v_i|\sigma (v_i)=t\}$
for any
![]() $t\leqslant k-1$
, then these
$t\leqslant k-1$
, then these
![]() $S_t$
form a partition of the vertices.
$S_t$
form a partition of the vertices.
Claim 3.5.
For
![]() $t\leqslant k-1$
,
$t\leqslant k-1$
,
![]() $|S_t|\leqslant k-t$
.
$|S_t|\leqslant k-t$
.
Proof of claim. Suppose
![]() $|S_t|\geqslant k+1-t$
, by the definition of
$|S_t|\geqslant k+1-t$
, by the definition of
![]() $S_t$
, we can pick vertices
$S_t$
, we can pick vertices
![]() $i_1\lt i_2\lt \cdots \lt i_{k+1-t}$
from
$i_1\lt i_2\lt \cdots \lt i_{k+1-t}$
from
![]() $S_t$
and a blue order-
$S_t$
and a blue order-
![]() $t$
path on vertices
$t$
path on vertices
![]() $i_{k+1-t}\lt \cdots \lt i_{k}$
. Note that
$i_{k+1-t}\lt \cdots \lt i_{k}$
. Note that
![]() $\chi (i_ui_v)=\mathrm{red}$
for any
$\chi (i_ui_v)=\mathrm{red}$
for any
![]() $1\leqslant u\lt v\leqslant k+1-t$
, as otherwise adding
$1\leqslant u\lt v\leqslant k+1-t$
, as otherwise adding
![]() $i_u$
to the blue path of order
$i_u$
to the blue path of order
![]() $t$
starting from
$t$
starting from
![]() $i_v$
yields a blue path of order
$i_v$
yields a blue path of order
![]() $t+1$
, a contradiction to
$t+1$
, a contradiction to
![]() $i_v\in S_t$
. Let
$i_v\in S_t$
. Let
![]() $D$
be the dependency digraph induced on the
$D$
be the dependency digraph induced on the
![]() $k$
vertices
$k$
vertices
![]() $i_1,\ldots ,i_k$
. By the definition of
$i_1,\ldots ,i_k$
. By the definition of
![]() $D$
, for any directed edge
$D$
, for any directed edge
![]() $(u,v)\in D$
, we must have
$(u,v)\in D$
, we must have
![]() $u\gt k+1-t$
and
$u\gt k+1-t$
and
![]() $v\leqslant k+1-t$
. Thus,
$v\leqslant k+1-t$
. Thus,
![]() $D$
is acyclic, a contradiction.
$D$
is acyclic, a contradiction.
Hence,
![]() ${{{k^2} - k + 2} \over 2} = \sum\limits_{t \in [k - 1]} | {S_t}| \leqslant \sum\limits_{t \in [k - 1]} {(k - t)} = {{{k^2} - k} \over 2},$
a contradiction.
${{{k^2} - k + 2} \over 2} = \sum\limits_{t \in [k - 1]} | {S_t}| \leqslant \sum\limits_{t \in [k - 1]} {(k - t)} = {{{k^2} - k} \over 2},$
a contradiction.
3.2. Proof of Theorem 3.2
By taking sufficiently small
![]() $c$
, we may assume that
$c$
, we may assume that
![]() $n$
is sufficiently large in terms of
$n$
is sufficiently large in terms of
![]() $k$
and
$k$
and
![]() $\eta .$
We define additional constants
$\eta .$
We define additional constants
![]() $c, \alpha , \beta , \gamma , \gamma _1, \gamma _2, \varepsilon , \varepsilon _1$
, such that
$c, \alpha , \beta , \gamma , \gamma _1, \gamma _2, \varepsilon , \varepsilon _1$
, such that
Suppose, for the sake of contradiction, that
![]() $\overline {G}$
does not contain a copy of
$\overline {G}$
does not contain a copy of
![]() ${K_2}[{{cn} \over {\log n}}]$
.
${K_2}[{{cn} \over {\log n}}]$
.
Claim 3.6.
![]() $G$
is
$G$
is
![]() $(\alpha , \beta )$
-dense.
$(\alpha , \beta )$
-dense.
Proof of claim. Suppose otherwise, so there is a set
![]() $S \subseteq V(G)$
with
$S \subseteq V(G)$
with
![]() $|S| \geqslant \alpha n$
and
$|S| \geqslant \alpha n$
and
![]() $e_G(S) \lt \beta \binom{|S|}{2}.$
Removing vertices of degree more than
$e_G(S) \lt \beta \binom{|S|}{2}.$
Removing vertices of degree more than
![]() $4 \beta |S|$
in
$4 \beta |S|$
in
![]() $G[S],$
we obtain a set
$G[S],$
we obtain a set
![]() $S'$
of size at least
$S'$
of size at least
![]() $|S| / 2 \geqslant \alpha n / 2$
such that
$|S| / 2 \geqslant \alpha n / 2$
such that
![]() $\Delta (G[S']) \lt 8 \beta |S'|.$
Then Theorem 1.1 implies the existence of
$\Delta (G[S']) \lt 8 \beta |S'|.$
Then Theorem 1.1 implies the existence of
![]() ${K_2}[{{cn} \over {\log n}}]$
in
${K_2}[{{cn} \over {\log n}}]$
in
![]() $\overline {G[S']}$
, contradicting our assumption.
$\overline {G[S']}$
, contradicting our assumption.
By Lemma 2.3, there exist sets
![]() $A_1, \dots , A_{f(k)} \subseteq V(G)$
such that
$A_1, \dots , A_{f(k)} \subseteq V(G)$
such that
![]() $A_1 \lt A_2 \lt \dots \lt A_{f(k)},$
for all
$A_1 \lt A_2 \lt \dots \lt A_{f(k)},$
for all
![]() $i \in [f(k)], |A_i| \geqslant \gamma _1 n$
and for all
$i \in [f(k)], |A_i| \geqslant \gamma _1 n$
and for all
![]() $1 \leqslant i \lt j \leqslant f(k),$
$1 \leqslant i \lt j \leqslant f(k),$
![]() $(A_i, A_j)$
is
$(A_i, A_j)$
is
![]() $\varepsilon _1$
-regular with density at least
$\varepsilon _1$
-regular with density at least
![]() ${\eta \over 2}$
in
${\eta \over 2}$
in
![]() $\overline {G}.$
$\overline {G}.$
We define an edge-colouring
![]() $\chi _0$
of the complete graph on the ordered vertex set
$\chi _0$
of the complete graph on the ordered vertex set
![]() $\{1,2,\ldots , f(k)\}$
as follows. For
$\{1,2,\ldots , f(k)\}$
as follows. For
![]() $1 \leqslant i \lt j \leqslant f(k)$
, let
$1 \leqslant i \lt j \leqslant f(k)$
, let
 \begin{align*}\chi _0(ij) = \begin{cases} \mathrm{blue}, &\text{if } d(A_i, A_j) \geqslant \beta ^2\\ \mathrm{red}, &\text{otherwise}. \end{cases} \end{align*}
\begin{align*}\chi _0(ij) = \begin{cases} \mathrm{blue}, &\text{if } d(A_i, A_j) \geqslant \beta ^2\\ \mathrm{red}, &\text{otherwise}. \end{cases} \end{align*}
By definition of
![]() $f(k),$
there exist indices
$f(k),$
there exist indices
![]() $a_1 \lt \dots \lt a_k$
such that
$a_1 \lt \dots \lt a_k$
such that
![]() $\chi _0[\{a_1, \dots , a_k\}]$
is admissible. For
$\chi _0[\{a_1, \dots , a_k\}]$
is admissible. For
![]() $i \in [k],$
let
$i \in [k],$
let
![]() $B_i = A_{a_i}.$
Moreover, define a colouring
$B_i = A_{a_i}.$
Moreover, define a colouring
![]() $\chi \colon \binom{[k]}{2} \rightarrow \{ \mathrm{red}, \mathrm{blue} \}$
by setting
$\chi \colon \binom{[k]}{2} \rightarrow \{ \mathrm{red}, \mathrm{blue} \}$
by setting
![]() $\chi (ij) = \chi _0(a_ia_j)$
and note that
$\chi (ij) = \chi _0(a_ia_j)$
and note that
![]() $\chi$
is admissible. We now show that we can either construct an induced monotone
$\chi$
is admissible. We now show that we can either construct an induced monotone
![]() $P_{2k}$
in
$P_{2k}$
in
![]() $G$
by placing two consecutive vertices in each set
$G$
by placing two consecutive vertices in each set
![]() $B_i$
or there is a biclique of size
$B_i$
or there is a biclique of size
![]() ${{cn} \over {\log n}}$
in
${{cn} \over {\log n}}$
in
![]() $\overline {G},$
thus obtaining a contradiction.
$\overline {G},$
thus obtaining a contradiction.
Recall that
![]() $|B_i| \geqslant \gamma _1 n \geqslant \alpha n,$
so since
$|B_i| \geqslant \gamma _1 n \geqslant \alpha n,$
so since
![]() $G$
is
$G$
is
![]() $(\alpha , \beta )$
-dense, we have
$(\alpha , \beta )$
-dense, we have
![]() $d(G[B_i]) \geqslant \beta .$
Applying Lemma 2.3 to
$d(G[B_i]) \geqslant \beta .$
Applying Lemma 2.3 to
![]() $G[B_i]$
for each
$G[B_i]$
for each
![]() $i \in [k],$
we obtain two sets
$i \in [k],$
we obtain two sets
![]() $C_{2i-1}, C_{2i} \subseteq B_i$
of size at least
$C_{2i-1}, C_{2i} \subseteq B_i$
of size at least
![]() $\gamma _2 |B_i| \geqslant \gamma _2 \gamma _1 n=\gamma n$
with
$\gamma _2 |B_i| \geqslant \gamma _2 \gamma _1 n=\gamma n$
with
![]() $C_{2i-1} \lt C_{2i}$
and such that
$C_{2i-1} \lt C_{2i}$
and such that
![]() $(C_{2i-1}, C_{2i})$
is
$(C_{2i-1}, C_{2i})$
is
![]() $\varepsilon$
-regular in
$\varepsilon$
-regular in
![]() $G$
with density at least
$G$
with density at least
![]() ${\beta \over 4}$
. To summarise, we have that
${\beta \over 4}$
. To summarise, we have that
![]() $C_1 \lt C_2 \lt \dots \lt C_{2k},$
$C_1 \lt C_2 \lt \dots \lt C_{2k},$
![]() $|C_i| \geqslant \gamma _2 |B_i| \geqslant \gamma n,$
for all
$|C_i| \geqslant \gamma _2 |B_i| \geqslant \gamma n,$
for all
![]() $i \in [2k].$
Moreover, using that
$i \in [2k].$
Moreover, using that
![]() ${{{\varepsilon _1}} \over {{\gamma _2}}}\lt \varepsilon $
, by Lemma 2.2, the pairs
${{{\varepsilon _1}} \over {{\gamma _2}}}\lt \varepsilon $
, by Lemma 2.2, the pairs
![]() $(C_i, C_j)$
are
$(C_i, C_j)$
are
![]() $\varepsilon$
-regular. Finally, the following holds for the densities between different pairs. Let
$\varepsilon$
-regular. Finally, the following holds for the densities between different pairs. Let
![]() $1 \leqslant i \lt j \leqslant 2k,$
then
$1 \leqslant i \lt j \leqslant 2k,$
then
-
a) If
 $\lfloor {{i \over 2}} \rfloor = \lfloor {{j \over 2}} \rfloor $
, then
$\lfloor {{i \over 2}} \rfloor = \lfloor {{j \over 2}} \rfloor $
, then
 $d({C_i},{C_j})\gt {\beta \over 4}$
.
$d({C_i},{C_j})\gt {\beta \over 4}$
. -
b) If
 $\lfloor {{i \over 2}} \rfloor \ne \lfloor {{j \over 2}} \rfloor $
, then
$\lfloor {{i \over 2}} \rfloor \ne \lfloor {{j \over 2}} \rfloor $
, then
 $d({C_i},{C_j})\lt 1 - {\eta \over 4}$
.
$d({C_i},{C_j})\lt 1 - {\eta \over 4}$
. -
c) If
 $\chi (\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{red}}$
, then
$\chi (\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{red}}$
, then
 $d(C_i, C_j) \lt 2 \beta ^2$
.
$d(C_i, C_j) \lt 2 \beta ^2$
. -
d) If
 $\chi (\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{blue}}$
, then
$\chi (\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{blue}}$
, then
 $d({C_i},{C_j})\gt {{{\beta ^2}} \over 2}$
.
$d({C_i},{C_j})\gt {{{\beta ^2}} \over 2}$
.
Let
![]() $D = D(\chi )$
be the dependency digraph of
$D = D(\chi )$
be the dependency digraph of
![]() $\chi$
as defined in Definition 3.1. By assumption,
$\chi$
as defined in Definition 3.1. By assumption,
![]() $D$
is acyclic. Consider a fixed topological ordering of
$D$
is acyclic. Consider a fixed topological ordering of
![]() $D$
and for
$D$
and for
![]() $i \in [k]$
, let
$i \in [k]$
, let
![]() $\pi (i)$
denote the position of vertex
$\pi (i)$
denote the position of vertex
![]() $i$
in this topological ordering. In other words, we have for every edge
$i$
in this topological ordering. In other words, we have for every edge
![]() $ij \in E(D)$
,
$ij \in E(D)$
,
![]() $\pi (i) \lt \pi (j)$
.
$\pi (i) \lt \pi (j)$
.
Let
![]() $(i_1, i_1+1), (i_2, i_2+1), \dots , (i_{k-1}, i_{k-1}+1)$
be an ordering of the edges
$(i_1, i_1+1), (i_2, i_2+1), \dots , (i_{k-1}, i_{k-1}+1)$
be an ordering of the edges
![]() $(1, 2), \dots , (k-1, k)$
according to the earliest appearance in
$(1, 2), \dots , (k-1, k)$
according to the earliest appearance in
![]() $\pi$
of one of their endpoints. In other words for
$\pi$
of one of their endpoints. In other words for
![]() $j \lt j',$
we have that
$j \lt j',$
we have that
![]() $\min \{\pi (i_j), \pi (i_j+1)\} \leqslant \min \{\pi (i_{j'}), \pi (i_{j'}+1)\}$
. In particular, when processing
$\min \{\pi (i_j), \pi (i_j+1)\} \leqslant \min \{\pi (i_{j'}), \pi (i_{j'}+1)\}$
. In particular, when processing
![]() $(i_t,i_t+1)$
, any
$(i_t,i_t+1)$
, any
![]() $j$
with
$j$
with
![]() $\chi ( {\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor } ) = \chi ( {\lfloor {{{i + 1} \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor }) = {\rm{blue}}$
must satisfy
$\chi ( {\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor } ) = \chi ( {\lfloor {{{i + 1} \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor }) = {\rm{blue}}$
must satisfy
![]() $j\in I_t$
by the definition of
$j\in I_t$
by the definition of
![]() $D$
and the choice of the order.
$D$
and the choice of the order.
We shall construct a monotone induced path
![]() $x_1, \dots , x_{2k}$
with
$x_1, \dots , x_{2k}$
with
![]() $x_j \in C_j$
for all
$x_j \in C_j$
for all
![]() $j \in [2k].$
We first embed all but
$j \in [2k].$
We first embed all but
![]() $x_1$
and
$x_1$
and
![]() $x_{2k}$
in
$x_{2k}$
in
![]() $k-1$
steps. At step
$k-1$
steps. At step
![]() $t \in [k-1],$
we shall define the vertices
$t \in [k-1],$
we shall define the vertices
![]() $x_{2i_t}, x_{2i_t+1}.$
Finally, we embed
$x_{2i_t}, x_{2i_t+1}.$
Finally, we embed
![]() $x_1$
and
$x_1$
and
![]() $x_{2k}.$
$x_{2k}.$
Let us now formally describe the embedding procedure. For each
![]() $t\in [k]$
, just before executing step
$t\in [k]$
, just before executing step
![]() $t$
we maintain the following invariants:
$t$
we maintain the following invariants:
-
(I1) The set of already embedded indices is
 \begin{align*}I_t \;=\; \bigcup _{j=1}^{t-1} \{\,2i_j,\; 2i_j+1\,\}\subseteq [2k]. \end{align*}
\begin{align*}I_t \;=\; \bigcup _{j=1}^{t-1} \{\,2i_j,\; 2i_j+1\,\}\subseteq [2k]. \end{align*}
-
(I2) For every
 $i\in [2k]{\setminus} I_t$
there is a candidate set
$i\in [2k]{\setminus} I_t$
there is a candidate set
 $C_i^t\subseteq C_i$
with the uniform lower bound
$C_i^t\subseteq C_i$
with the uniform lower bound \begin{align*}|C_i^t|\;\geqslant \; \beta ^{8(t-1)}\,|C_i|. \end{align*}
\begin{align*}|C_i^t|\;\geqslant \; \beta ^{8(t-1)}\,|C_i|. \end{align*}
-
(I3) For any distinct
 $i,j\in [2k]{\setminus} I_t$
, the pair
$i,j\in [2k]{\setminus} I_t$
, the pair
 $(C_i^t,C_j^t)$
is regular (with parameter at most
$(C_i^t,C_j^t)$
is regular (with parameter at most
 $\varepsilon$
; and by Lemma 2.2 and the parameter hierarchy, whenever invoked below we may in fact use
$\varepsilon$
; and by Lemma 2.2 and the parameter hierarchy, whenever invoked below we may in fact use
 $\varepsilon ^{0.9}$
). We also repeatedly use the density bounds a)–d) for the base pairs
$\varepsilon ^{0.9}$
). We also repeatedly use the density bounds a)–d) for the base pairs
 $(C_i,C_j)$
.
$(C_i,C_j)$
.
Formally, we initialise with
![]() $C_i^1=C_i$
for all
$C_i^1=C_i$
for all
![]() $i\in [2k]$
. After
$i\in [2k]$
. After
![]() $t-1$
steps, for each
$t-1$
steps, for each
![]() $i\in [2k]$
we define
$i\in [2k]$
we define
Here we require adjacency only to those of
![]() $x_{i-1},x_{i+1}$
that have already been embedded (i.e.,
$x_{i-1},x_{i+1}$
that have already been embedded (i.e.,
![]() $j\in I_t\cap \{i-1,i+1\}$
), and we delete vertices adjacent to any other already embedded
$j\in I_t\cap \{i-1,i+1\}$
), and we delete vertices adjacent to any other already embedded
![]() $x_j$
(i.e.,
$x_j$
(i.e.,
![]() $j\in I_t{\setminus} \{i-1,i+1\}$
).
$j\in I_t{\setminus} \{i-1,i+1\}$
).
Given that we have run the procedure for
![]() $t-1 \leqslant k-2$
steps we show we can run step
$t-1 \leqslant k-2$
steps we show we can run step
![]() $t.$
Let
$t.$
Let
![]() $i = 2i_t$
and recall that we aim to embed vertices
$i = 2i_t$
and recall that we aim to embed vertices
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}.$
By assumption, we have sets
$x_{i+1}.$
By assumption, we have sets
![]() $C^t_i$
and
$C^t_i$
and
![]() $C^t_{i+1}$
of size at least
$C^t_{i+1}$
of size at least
![]() $\beta ^{8(t-1)} |C_i|$
into which we can embed the vertices
$\beta ^{8(t-1)} |C_i|$
into which we can embed the vertices
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
, respectively. Note that
$x_{i+1}$
, respectively. Note that
which implies that for all
![]() $i, j \in [2k] {\setminus} I_t, i \neq j,$
the pair
$i, j \in [2k] {\setminus} I_t, i \neq j,$
the pair
![]() $(C^t_i, C^t_j)$
is
$(C^t_i, C^t_j)$
is
![]() $\varepsilon ^{0.9}$
-regular.
$\varepsilon ^{0.9}$
-regular.
By the
![]() $\varepsilon ^{0.9}$
-regularity of
$\varepsilon ^{0.9}$
-regularity of
![]() $(C_i^t,C_j^t)$
, all but at most
$(C_i^t,C_j^t)$
, all but at most
![]() $\varepsilon ^{0.9}|C_i^t|$
vertices
$\varepsilon ^{0.9}|C_i^t|$
vertices
![]() $v\in C_i^t$
satisfy
$v\in C_i^t$
satisfy
By Lemma 2.2 applied to
![]() $(C_i,C_j)$
with subsets
$(C_i,C_j)$
with subsets
![]() $(C_i^t,C_j^t)$
we also have
$(C_i^t,C_j^t)$
we also have
Hence, for all but at most
![]() $\varepsilon ^{0.9}|C_i^t|$
vertices
$\varepsilon ^{0.9}|C_i^t|$
vertices
![]() $v\in C_i^t$
,
$v\in C_i^t$
,
where the last inequality follows from the parameter hierarchy. Discarding the exceptional vertices for each of the fewer than
![]() $2k$
choices of
$2k$
choices of
![]() $j$
and intersecting over
$j$
and intersecting over
![]() $j$
, we obtain a set
$j$
, we obtain a set
such that for every
![]() $v\in C_i'$
and
$v\in C_i'$
and
![]() $j\in [2k]{\setminus} (I_t\cup \{i,i+1\})$
,
$j\in [2k]{\setminus} (I_t\cup \{i,i+1\})$
,
Now we consider two cases.
Case 1.
![]() $\chi (i_t, i_t+1) = \mathrm{blue}$
.
$\chi (i_t, i_t+1) = \mathrm{blue}$
.
Note that
![]() $\lfloor {{i \over 2}} \rfloor = {i_t}$
and
$\lfloor {{i \over 2}} \rfloor = {i_t}$
and
![]() $\lfloor {{{i + 1} \over 2}} \rfloor = {i_t} + 1$
. By condition d), we have
$\lfloor {{{i + 1} \over 2}} \rfloor = {i_t} + 1$
. By condition d), we have
![]() $d({C_i},{C_{i + 1}})\gt {{{\beta ^2}} \over 2}$
and thus by
$d({C_i},{C_{i + 1}})\gt {{{\beta ^2}} \over 2}$
and thus by
![]() $\varepsilon$
-regularity and choices of parameters,
$\varepsilon$
-regularity and choices of parameters,
![]() $d({C'_i},{C'_{i + 1}})\gt {{{\beta ^2}} \over 2} - \sqrt \varepsilon \gt {\beta ^3}.$
In particular, there is a vertex
$d({C'_i},{C'_{i + 1}})\gt {{{\beta ^2}} \over 2} - \sqrt \varepsilon \gt {\beta ^3}.$
In particular, there is a vertex
![]() $u \in C'_i$
with
$u \in C'_i$
with
![]() $|N(u) \cap {C'_{i + 1}}| \geqslant {{{\beta ^3}} \over 2} \cdot |{C'_{i + 1}}|$
. Pick such a vertex
$|N(u) \cap {C'_{i + 1}}| \geqslant {{{\beta ^3}} \over 2} \cdot |{C'_{i + 1}}|$
. Pick such a vertex
![]() $u.$
For
$u.$
For
![]() $j \in [2k] {\setminus} (I_t \cup \{i-1, i, i+1\})$
, let
$j \in [2k] {\setminus} (I_t \cup \{i-1, i, i+1\})$
, let
![]() $C'_j = C^t_j {\setminus} N(u).$
Furthermore, define
$C'_j = C^t_j {\setminus} N(u).$
Furthermore, define
![]() $C'_{i-1} = C^t_{i-1} \cap N_G(u)$
if
$C'_{i-1} = C^t_{i-1} \cap N_G(u)$
if
![]() $i-1 \not \in I_t$
.
$i-1 \not \in I_t$
.
Recall that
![]() $d({C_i},{C_j})\lt 1 - {\eta \over 4}$
for
$d({C_i},{C_j})\lt 1 - {\eta \over 4}$
for
![]() $j \in [2k] {\setminus} (I_t \cup \{i-1, i, i+1\})$
by condition b) and
$j \in [2k] {\setminus} (I_t \cup \{i-1, i, i+1\})$
by condition b) and
![]() $d({C_{i - 1}},{C_i})\gt {\beta \over 4}$
by condition a). Therefore, for all
$d({C_{i - 1}},{C_i})\gt {\beta \over 4}$
by condition a). Therefore, for all
![]() $j \in [2k] {\setminus} (I_t \cup \{i, i+1\}),$
combining with
$j \in [2k] {\setminus} (I_t \cup \{i, i+1\}),$
combining with
![]() $(\clubsuit )$
we have
$(\clubsuit )$
we have
By
![]() $\varepsilon$
-regularity, there is a vertex
$\varepsilon$
-regularity, there is a vertex
![]() $v \in N(u) \cap C'_{i+1}$
such that for all
$v \in N(u) \cap C'_{i+1}$
such that for all
![]() $j \in [2k] {\setminus} (I_t \cup \{i, i+1\}),$
we have
$j \in [2k] {\setminus} (I_t \cup \{i, i+1\}),$
we have
Pick such a vertex
![]() $v$
and let
$v$
and let
![]() $x_i = u$
and
$x_i = u$
and
![]() $x_{i+1} = v.$
Recalling that
$x_{i+1} = v.$
Recalling that
![]() $d({C_{i + 1}},{C_j})\lt 1 - {\eta \over 4}$
for
$d({C_{i + 1}},{C_j})\lt 1 - {\eta \over 4}$
for
![]() $j \neq i+2$
and
$j \neq i+2$
and
![]() $d({C_{i + 1}},{C_{i + 2}})\gt {\beta \over 4}$
, it follows that
$d({C_{i + 1}},{C_{i + 2}})\gt {\beta \over 4}$
, it follows that
![]() $|C^{t+1}_j| \geqslant \beta ^{8t} \cdot |C^t_j|$
for all
$|C^{t+1}_j| \geqslant \beta ^{8t} \cdot |C^t_j|$
for all
![]() $j \in [2k] {\setminus} I_{t+1}$
as needed.
$j \in [2k] {\setminus} I_{t+1}$
as needed.
Case 2.
![]() $\chi (i_t, i_t+1) = \mathrm{red}$
.
$\chi (i_t, i_t+1) = \mathrm{red}$
.
Since
![]() $|{C'_i}|,|{C'_{i + 1}}| \geqslant {1 \over 2} \cdot {\beta ^{8(t - 1)}}\gamma n\gt {n \over {\log n}}$
and
$|{C'_i}|,|{C'_{i + 1}}| \geqslant {1 \over 2} \cdot {\beta ^{8(t - 1)}}\gamma n\gt {n \over {\log n}}$
and
![]() $\overline {G}$
is
$\overline {G}$
is
![]() ${K_2}[{{cn} \over {\log n}}]$
-free, there exists an edge
${K_2}[{{cn} \over {\log n}}]$
-free, there exists an edge
![]() $uv \in E(G)$
with
$uv \in E(G)$
with
![]() $u \in C'_i, v \in C'_{i+1}.$
Set
$u \in C'_i, v \in C'_{i+1}.$
Set
![]() $x_i = u, x_{i+1} = v.$
We will show that for all
$x_i = u, x_{i+1} = v.$
We will show that for all
![]() $j \in [2k] {\setminus} I_{t+1},$
$j \in [2k] {\setminus} I_{t+1},$
![]() $|C^{t+1}_j| \geqslant \beta ^8 |C^t_j|$
, which is sufficient by our assumption.
$|C^{t+1}_j| \geqslant \beta ^8 |C^t_j|$
, which is sufficient by our assumption.
Consider first
![]() $j = i-1.$
If
$j = i-1.$
If
![]() $j \not \in [2k] {\setminus} I_t,$
there is nothing to prove. Otherwise,
$j \not \in [2k] {\setminus} I_t,$
there is nothing to prove. Otherwise,
![]() ${d_G}({C_j},{C_i})\gt {\beta \over 4}$
by condition a) and
${d_G}({C_j},{C_i})\gt {\beta \over 4}$
by condition a) and
![]() $d(C_j, C_{i+1}) \lt 2 \beta ^2$
by condition c). Hence, by the definitions of the sets
$d(C_j, C_{i+1}) \lt 2 \beta ^2$
by condition c). Hence, by the definitions of the sets
![]() $C'_i, C'_{i+1},$
we have
$C'_i, C'_{i+1},$
we have
Completely analogously, if
![]() $i+2 \in [2k] {\setminus} I_{t},$
we have
$i+2 \in [2k] {\setminus} I_{t},$
we have
![]() $|C^{t+1}_{i+2}| \geqslant \beta ^8 |C^t_{i+2}|.$
$|C^{t+1}_{i+2}| \geqslant \beta ^8 |C^t_{i+2}|.$
Now, consider
![]() $j \in [2k] {\setminus} (I_{t} \cup \{i-1, i+2\})$
. If
$j \in [2k] {\setminus} (I_{t} \cup \{i-1, i+2\})$
. If
![]() $\chi (\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{red}}$
or
$\chi (\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{red}}$
or
![]() $\chi (\lfloor {{{i + 1} \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{red}},$
then
$\chi (\lfloor {{{i + 1} \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{red}},$
then
![]() $d({C_i},{C_j}) + d({C_{i + 1}},{C_j})\lt 2{\beta ^2} + 1 - {\eta \over 4}$
and so combining with
$d({C_i},{C_j}) + d({C_{i + 1}},{C_j})\lt 2{\beta ^2} + 1 - {\eta \over 4}$
and so combining with
![]() $(\clubsuit )$
, we have
$(\clubsuit )$
, we have
as needed. Then we can assume that
![]() $\chi (\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = \chi (\lfloor {{{i + 1} \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{blue}}$
. Then by definition, we can see that
$\chi (\lfloor {{i \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = \chi (\lfloor {{{i + 1} \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor ) = {\rm{blue}}$
. Then by definition, we can see that
![]() $(\lfloor {{j \over 2}} \rfloor ,\lfloor {{i \over 2}} \rfloor ),(\lfloor {{j \over 2}} \rfloor ,\lfloor {{{i + 1} \over 2}} \rfloor ) \in E(D)$
, which implies that
$(\lfloor {{j \over 2}} \rfloor ,\lfloor {{i \over 2}} \rfloor ),(\lfloor {{j \over 2}} \rfloor ,\lfloor {{{i + 1} \over 2}} \rfloor ) \in E(D)$
, which implies that
![]() $\pi (\lfloor {{j \over 2}} \rfloor )\lt \pi (\lfloor {{i \over 2}} \rfloor),$
$\pi (\lfloor {{j \over 2}} \rfloor )\lt \pi (\lfloor {{i \over 2}} \rfloor),$
![]() $ \pi (\lfloor {{{i + 1} \over 2}} \rfloor )$
. Therefore,
$ \pi (\lfloor {{{i + 1} \over 2}} \rfloor )$
. Therefore,
![]() $(\lfloor {{j \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor + 1)$
appears before
$(\lfloor {{j \over 2}} \rfloor ,\lfloor {{j \over 2}} \rfloor + 1)$
appears before
![]() $\lfloor {{i \over 2}} \rfloor ,\lfloor {{i \over 2}} \rfloor + 1$
in the sequence
$\lfloor {{i \over 2}} \rfloor ,\lfloor {{i \over 2}} \rfloor + 1$
in the sequence
![]() $(i_1, i_1+1), \dots , (i_{k-1}, i_{k-1}+1)$
which in turn implies that
$(i_1, i_1+1), \dots , (i_{k-1}, i_{k-1}+1)$
which in turn implies that
![]() $j \in I_t,$
contradicting our assumption.
$j \in I_t,$
contradicting our assumption.
We have shown that we can run all
![]() $k-1$
steps of the above procedure. Finally, we have two candidate sets
$k-1$
steps of the above procedure. Finally, we have two candidate sets
![]() $C^k_1, C^k_{2k}$
of size at least
$C^k_1, C^k_{2k}$
of size at least
![]() $\beta ^{8k} \gamma _2 |B_1|$
into which we can embed the vertices
$\beta ^{8k} \gamma _2 |B_1|$
into which we can embed the vertices
![]() $x_1$
and
$x_1$
and
![]() $x_{2k}$
respectively. Recalling that
$x_{2k}$
respectively. Recalling that
![]() $d({C_1},{C_{2k}})\lt 1 - {\eta \over 4}$
, by
$d({C_1},{C_{2k}})\lt 1 - {\eta \over 4}$
, by
![]() $\varepsilon _1$
-regularity, there are vertices
$\varepsilon _1$
-regularity, there are vertices
![]() $u \in C^k_1, v \in C^k_{2k}$
such that
$u \in C^k_1, v \in C^k_{2k}$
such that
![]() $uv \not \in E(G).$
Setting
$uv \not \in E(G).$
Setting
![]() $x_1 = u, x_{2k} = v,$
we have that
$x_1 = u, x_{2k} = v,$
we have that
![]() $x_1, x_2, \dots , x_{2k}$
is a monotone induced path in
$x_1, x_2, \dots , x_{2k}$
is a monotone induced path in
![]() $G$
, contradicting our assumption.
$G$
, contradicting our assumption.
This finishes the proof of Theorem 3.2.
4. Lower bound construction for Theorem 1.4
In this section, we proceed to construct
![]() $n$
-vertex ordered graphs
$n$
-vertex ordered graphs
![]() $G$
with no induced monotone path
$G$
with no induced monotone path
![]() $P_{2k-1}$
such that its complement
$P_{2k-1}$
such that its complement
![]() $\overline {G}$
has positive
$\overline {G}$
has positive
![]() ${K_{\lfloor {{{{k^2}} \over 4}} \rfloor }}$
-density and no biclique of size
${K_{\lfloor {{{{k^2}} \over 4}} \rfloor }}$
-density and no biclique of size
![]() $n/e^{o(\sqrt {\log n/\log \log n})}$
.
$n/e^{o(\sqrt {\log n/\log \log n})}$
.
Now let
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
![]() $n$
be sufficiently large,
$n$
be sufficiently large,
![]() $h = {{\log n} \over {\log \log n}}$
and
$h = {{\log n} \over {\log \log n}}$
and
![]() $\mu = {\varepsilon \over {\sqrt h }}$
. Set
$\mu = {\varepsilon \over {\sqrt h }}$
. Set
![]() $s = \lfloor {{k \over 2}} \rfloor $
and
$s = \lfloor {{k \over 2}} \rfloor $
and
![]() $t = \lfloor {{k \over 2}} \rfloor $
. For simplicity, we only provide the proof details for even
$t = \lfloor {{k \over 2}} \rfloor $
. For simplicity, we only provide the proof details for even
![]() $k$
so that the floors/ceilings can be dropped; the argument for odd
$k$
so that the floors/ceilings can be dropped; the argument for odd
![]() $k$
is identical.
$k$
is identical.
Construction. By Lemma 2.8, as
![]() $n$
is sufficiently large, we can partition the unit sphere
$n$
is sufficiently large, we can partition the unit sphere
![]() $\mathbb{S}^{h-1}$
into
$\mathbb{S}^{h-1}$
into
![]() ${{2n} \over k}$
many pieces
${{2n} \over k}$
many pieces
![]() ${D_1},{D_2}, \ldots ,{D_{{{2n} \over k}}}$
of equal measure such that each piece has diameter at most
${D_1},{D_2}, \ldots ,{D_{{{2n} \over k}}}$
of equal measure such that each piece has diameter at most
![]() ${\mu \over 4}$
. We construct
${\mu \over 4}$
. We construct
![]() $V(G)=V_{1}\sqcup V_{2}\sqcup \cdots \sqcup V_{s}$
as follows. For each
$V(G)=V_{1}\sqcup V_{2}\sqcup \cdots \sqcup V_{s}$
as follows. For each
![]() $i\in [s]$
, we select an arbitrary point from each
$i\in [s]$
, we select an arbitrary point from each
![]() $D_{j}$
,
$D_{j}$
,
![]() $j \in [{{2n} \over k}]$
, as a vertex. So each
$j \in [{{2n} \over k}]$
, as a vertex. So each
![]() $V_{i}$
consists of
$V_{i}$
consists of
![]() ${{2n} \over k}$
vertices. We randomly partition each
${{2n} \over k}$
vertices. We randomly partition each
![]() $V_{i}=V_{i}^{(1)}\sqcup V_{i}^{(2)}\sqcup \cdots \sqcup V_{i}^{(t)}$
into
$V_{i}=V_{i}^{(1)}\sqcup V_{i}^{(2)}\sqcup \cdots \sqcup V_{i}^{(t)}$
into
![]() $t$
parts of equal size. Moreover, we label the vertices so that
$t$
parts of equal size. Moreover, we label the vertices so that
![]() $V_{1}\lt V_{2}\lt \cdots \lt V_{s}$
and for each
$V_{1}\lt V_{2}\lt \cdots \lt V_{s}$
and for each
![]() $i\in [s]$
,
$i\in [s]$
,
![]() $V_{i}^{(1)}\lt V_{i}^{(2)}\lt \cdots \lt V_{i}^{(t)}$
. For convenience, for a pair of vertices
$V_{i}^{(1)}\lt V_{i}^{(2)}\lt \cdots \lt V_{i}^{(t)}$
. For convenience, for a pair of vertices
![]() $x,y\in V(G)$
, we write
$x,y\in V(G)$
, we write
![]() $|x-y|$
for the distance between the corresponding points on the sphere.
$|x-y|$
for the distance between the corresponding points on the sphere.
The edge set of
![]() $G$
consists of the following three types of edges; see Fig. 2.
$G$
consists of the following three types of edges; see Fig. 2.
-
1. For each
 $1\leqslant i\leqslant s$
and
$1\leqslant i\leqslant s$
and
 $1\leqslant j\leqslant t$
,
$1\leqslant j\leqslant t$
,
 $G[V_{i}^{(j)}]$
is a clique.
$G[V_{i}^{(j)}]$
is a clique. -
2. For given
 $1\leqslant i\leqslant s$
and
$1\leqslant i\leqslant s$
and
 $j_{1}\neq j_{2}$
,
$j_{1}\neq j_{2}$
,
 $x\in V_{i}^{(j_{1})}$
and
$x\in V_{i}^{(j_{1})}$
and
 $y\in V_{i}^{(j_{2})}$
are adjacent if
$y\in V_{i}^{(j_{2})}$
are adjacent if
 $|x-y|\geqslant 2-\mu$
.
$|x-y|\geqslant 2-\mu$
. -
3. For given
 $i_{1}\neq i_{2}$
,
$i_{1}\neq i_{2}$
,
 $x\in V_{i_{1}}$
and
$x\in V_{i_{1}}$
and
 $y\in V_{i_{2}}$
are adjacent if
$y\in V_{i_{2}}$
are adjacent if
 $|x-y|\gt \sqrt {2}-\mu$
.
$|x-y|\gt \sqrt {2}-\mu$
.

Figure 2. The black shading represents a clique and is of type-1, the red and blue edges are of type-2 and 3 respectively.
Claim 4.1.
![]() $G$
does not contain induced monotone
$G$
does not contain induced monotone
![]() $P_{2k-1}$
.
$P_{2k-1}$
.
Proof of claim. Suppose
![]() $P$
is an induced monotone
$P$
is an induced monotone
![]() $P_{2k-1}$
on vertices
$P_{2k-1}$
on vertices
![]() $a_{1}\lt a_{2}\lt \cdots \lt a_{2k-1}$
. Note first that as each
$a_{1}\lt a_{2}\lt \cdots \lt a_{2k-1}$
. Note first that as each
![]() $V_i^{(j)}$
induces a clique, it contains at most two vertices of the induced path
$V_i^{(j)}$
induces a clique, it contains at most two vertices of the induced path
![]() $P$
. Thus
$P$
. Thus
![]() $P$
has at most
$P$
has at most
![]() $2\cdot t=k$
vertices in each
$2\cdot t=k$
vertices in each
![]() $V_i$
,
$V_i$
,
![]() $i\in [s]$
. Consequently, if all but at most one
$i\in [s]$
. Consequently, if all but at most one
![]() $p_i=|V(P)\cap V_i|$
,
$p_i=|V(P)\cap V_i|$
,
![]() $i\in [s]$
, are at most 2, then
$i\in [s]$
, are at most 2, then
![]() $|P|=\sum _{i\in [s]}p_i\leqslant k+2(s-1)=2k-2$
, a contradiction. We may then assume that at least two
$|P|=\sum _{i\in [s]}p_i\leqslant k+2(s-1)=2k-2$
, a contradiction. We may then assume that at least two
![]() $p_i$
are at least 3. Note that as
$p_i$
are at least 3. Note that as
![]() $V_{1}\lt V_{2}\lt \cdots \lt V_{s}$
, each
$V_{1}\lt V_{2}\lt \cdots \lt V_{s}$
, each
![]() $V_i$
must contain consecutive vertices in
$V_i$
must contain consecutive vertices in
![]() $P$
.
$P$
.
By definitions of type-2 and type-3 edges, there cannot be two type-2 edges
![]() $aa'\in V_i$
and
$aa'\in V_i$
and
![]() $bb'\in V_j$
with
$bb'\in V_j$
with
![]() $i\neq j$
such that
$i\neq j$
such that
![]() $ab,ab',a'b,a'b'\not \in E(G)$
due to Theorem 2.9.
$ab,ab',a'b,a'b'\not \in E(G)$
due to Theorem 2.9.
We claim that if any
![]() $p_i\geqslant 3$
, then
$p_i\geqslant 3$
, then
![]() $P[V_i]$
contains a type-2 edge. To see this, say
$P[V_i]$
contains a type-2 edge. To see this, say
![]() $a_r,a_{r+1},a_{r+2} \in P\cap V_i$
. Then these three vertices cannot be in the same
$a_r,a_{r+1},a_{r+2} \in P\cap V_i$
. Then these three vertices cannot be in the same
![]() $V_{i}^{(j)}$
for any
$V_{i}^{(j)}$
for any
![]() $j\in [t]$
as
$j\in [t]$
as
![]() $V_i^{(j)}$
induces a clique. Then at least one of the edges
$V_i^{(j)}$
induces a clique. Then at least one of the edges
![]() $a_{r}a_{r+1}$
and
$a_{r}a_{r+1}$
and
![]() $a_{r+1}a_{r+2}$
is of type-2.
$a_{r+1}a_{r+2}$
is of type-2.
If there are at least three say
![]() $p_i,p_j,p_{\ell }\geqslant 3$
with
$p_i,p_j,p_{\ell }\geqslant 3$
with
![]() $i\lt j\lt \ell$
. Then by the above discussion, there exist type-2 edges
$i\lt j\lt \ell$
. Then by the above discussion, there exist type-2 edges
![]() $e$
in
$e$
in
![]() $P[V_i]$
and
$P[V_i]$
and
![]() $e'$
in
$e'$
in
![]() $P[V_{\ell }]$
. Moreover, as
$P[V_{\ell }]$
. Moreover, as
![]() $p_j\gt 0$
, there are no edges between these type-2 edges
$p_j\gt 0$
, there are no edges between these type-2 edges
![]() $e$
and
$e$
and
![]() $e'$
, contradicting Theorem 2.9.
$e'$
, contradicting Theorem 2.9.
Thus, we may assume that exactly two, say
![]() $V_1, V_2$
, containing at least
$V_1, V_2$
, containing at least
![]() $3$
vertices of
$3$
vertices of
![]() $P$
, and the remaining parts contain at most
$P$
, and the remaining parts contain at most
![]() $2$
vertices each. If
$2$
vertices each. If
![]() $p_1=p_2=3$
, then
$p_1=p_2=3$
, then
![]() $|P|\leqslant 3+3+2(s-2)\leqslant k+2\leqslant 2k-2$
as
$|P|\leqslant 3+3+2(s-2)\leqslant k+2\leqslant 2k-2$
as
![]() $k\geqslant 4$
. Thus, without loss of generality
$k\geqslant 4$
. Thus, without loss of generality
![]() $p_1\geqslant 4$
and so
$p_1\geqslant 4$
and so
![]() $a_1,a_2,a_3,a_4\in P[V_1]$
. Then
$a_1,a_2,a_3,a_4\in P[V_1]$
. Then
![]() $\{a_1,a_2,a_3\}$
and
$\{a_1,a_2,a_3\}$
and
![]() $P[V_2]$
both contain a type-2 edge and there is no edge between these two edges because of
$P[V_2]$
both contain a type-2 edge and there is no edge between these two edges because of
![]() $a_4$
, again contradicting Theorem 2.9.
$a_4$
, again contradicting Theorem 2.9.
Next, we verify that there is no large biclique in
![]() $\overline {G}$
.
$\overline {G}$
.
Claim 4.2.
![]() $\overline {G}$
does not contain
$\overline {G}$
does not contain
![]() ${K_2}[{{cn} \over {\log n}}]$
as a subgraph.
${K_2}[{{cn} \over {\log n}}]$
as a subgraph.
Proof of claim. Suppose there is a copy of
![]() ${K_2}[{{cn} \over {\log n}}]$
in
${K_2}[{{cn} \over {\log n}}]$
in
![]() $\overline {G}$
. By pigeonhole principle, there is a copy of
$\overline {G}$
. By pigeonhole principle, there is a copy of
![]() ${K_2}[{{cn} \over {k\log n}}]$
in
${K_2}[{{cn} \over {k\log n}}]$
in
![]() $\overline {G}$
with parts
$\overline {G}$
with parts
![]() $S\subseteq V_i$
and
$S\subseteq V_i$
and
![]() $T\subseteq V_j$
.
$T\subseteq V_j$
.
If
![]() $i=j$
, then by pigeonhole principle again, there exist
$i=j$
, then by pigeonhole principle again, there exist
![]() $a,b\in [t]$
such that
$a,b\in [t]$
such that
![]() $\overline {G}$
contains a copy of
$\overline {G}$
contains a copy of
![]() ${K_2}[{{2cn} \over {{k^2}\log n}}]$
with parts
${K_2}[{{2cn} \over {{k^2}\log n}}]$
with parts
![]() $S_{a}\subseteq V_{i}^{(a)}$
and
$S_{a}\subseteq V_{i}^{(a)}$
and
![]() $T_{b}\subseteq V_{i}^{(b)}$
. Note that the Lebesgue measures of the pieces
$T_{b}\subseteq V_{i}^{(b)}$
. Note that the Lebesgue measures of the pieces
![]() $D_j$
,
$D_j$
,
![]() $j \in [{{2n} \over k}]$
, corresponding to both
$j \in [{{2n} \over k}]$
, corresponding to both
![]() $S_{a}$
and
$S_{a}$
and
![]() $T_{b}$
are at least
$T_{b}$
are at least
![]() ${{2cn} \over {{k^2}\log n}} \cdot {k \over {2n}}\gt {e^{{{ - h\mu } \over 4}}}$
, therefore, by Lemma 2.5,
${{2cn} \over {{k^2}\log n}} \cdot {k \over {2n}}\gt {e^{{{ - h\mu } \over 4}}}$
, therefore, by Lemma 2.5,
![]() ${d_{\max }}({S_a},{T_b}) \geqslant 2 - {\mu \over 2}$
. This, together with the fact that the diameter of each piece
${d_{\max }}({S_a},{T_b}) \geqslant 2 - {\mu \over 2}$
. This, together with the fact that the diameter of each piece
![]() $D_j$
is at most
$D_j$
is at most
![]() $\mu /4$
, implies that there must be a type-2 edge
$\mu /4$
, implies that there must be a type-2 edge
![]() $uv$
with
$uv$
with
![]() $u\in S_{a}$
,
$u\in S_{a}$
,
![]() $v\in T_{b}$
, a contradiction.
$v\in T_{b}$
, a contradiction.
If
![]() $i\neq j$
, then both of the Lebesgue measures of
$i\neq j$
, then both of the Lebesgue measures of
![]() $S$
and
$S$
and
![]() $T$
are at least
$T$
are at least
![]() ${{cn} \over {k\log n}} \cdot {k \over {2n}}\gt {e^{{{ - h\mu } \over 4}}}$
. Therefore the diameters of
${{cn} \over {k\log n}} \cdot {k \over {2n}}\gt {e^{{{ - h\mu } \over 4}}}$
. Therefore the diameters of
![]() $S$
and
$S$
and
![]() $T$
are at least
$T$
are at least
![]() $2 - {\mu \over 2}$
. We can then find
$2 - {\mu \over 2}$
. We can then find
![]() $x,x'\in S\subseteq V_{i}$
and
$x,x'\in S\subseteq V_{i}$
and
![]() $y,y'\in T\subseteq V_{j}$
with
$y,y'\in T\subseteq V_{j}$
with
![]() $|x-x'|,|y-y'|\geqslant 2-\mu$
. Moreover, by definition of
$|x-x'|,|y-y'|\geqslant 2-\mu$
. Moreover, by definition of
![]() $G$
, all of pairs
$G$
, all of pairs
![]() $xy,xy',x'y,x'y'\notin E(G)$
implies that all of the distances
$xy,xy',x'y,x'y'\notin E(G)$
implies that all of the distances
![]() $|x-y|$
,
$|x-y|$
,
![]() $|x-y'|$
,
$|x-y'|$
,
![]() $|x'-y|$
and
$|x'-y|$
and
![]() $|x'-y'|$
are at most
$|x'-y'|$
are at most
![]() $\sqrt {2}-\mu$
, contradicting Theorem 2.9.
$\sqrt {2}-\mu$
, contradicting Theorem 2.9.
Claim 4.3.
The expected number of
![]() ${{{k^2}} \over 4}$
-cliques in
${{{k^2}} \over 4}$
-cliques in
![]() $\overline {G}$
is at least
$\overline {G}$
is at least
![]() $\eta {n^{{{{k^2}} \over 4}}}$
for some
$\eta {n^{{{{k^2}} \over 4}}}$
for some
![]() $\eta \gt 0$
.
$\eta \gt 0$
.
Proof of claim. The number of
![]() ${{{k^2}} \over 4}$
-cliques in
${{{k^2}} \over 4}$
-cliques in
![]() $\overline {G}$
is at least the number of
$\overline {G}$
is at least the number of
![]() ${{{k^2}} \over 4}$
-tuples
${{{k^2}} \over 4}$
-tuples
![]() $(v_{i}^{(j)}\,:\,i\in [s],$
$(v_{i}^{(j)}\,:\,i\in [s],$
![]() $j\in [t])$
with
$j\in [t])$
with
![]() $v_{i}^{(j)}\in V_{i}^{(j)}$
such that the following conditions hold.
$v_{i}^{(j)}\in V_{i}^{(j)}$
such that the following conditions hold.
-
• For each
 $1\leqslant i\leqslant s$
, we have
$1\leqslant i\leqslant s$
, we have
 $|v_{i}^{(j_{1})}-v_{i}^{(j_{2})}|\lt 2-\mu$
for any
$|v_{i}^{(j_{1})}-v_{i}^{(j_{2})}|\lt 2-\mu$
for any
 $1\leqslant j_{1}\lt j_{2}\leqslant t$
.
$1\leqslant j_{1}\lt j_{2}\leqslant t$
. -
• For each
 $1\leqslant i_{1}\lt i_{2}\leqslant s$
, we have
$1\leqslant i_{1}\lt i_{2}\leqslant s$
, we have
 $|v_{i_{1}}^{(j_{1})}-v_{i_{2}}^{(j_{2})}|\leqslant \sqrt {2}-\mu$
for any
$|v_{i_{1}}^{(j_{1})}-v_{i_{2}}^{(j_{2})}|\leqslant \sqrt {2}-\mu$
for any
 $j_{1},j_{2}\in [t]$
.
$j_{1},j_{2}\in [t]$
.
For each
![]() $1\leqslant i\leqslant s$
and
$1\leqslant i\leqslant s$
and
![]() $1\leqslant j\leqslant t$
, take an arbitrary vertex
$1\leqslant j\leqslant t$
, take an arbitrary vertex
![]() $a_{i}^{(j)}\in V_{i}^{(j)}$
. As
$a_{i}^{(j)}\in V_{i}^{(j)}$
. As
![]() $V_{i}^{(j)}$
,
$V_{i}^{(j)}$
,
![]() $j\in [t]$
, is a random partition of
$j\in [t]$
, is a random partition of
![]() $V_i$
, we have by Lemma 2.6 that for every
$V_i$
, we have by Lemma 2.6 that for every
![]() $1\leqslant i_{1}\lt i_{2}\leqslant s$
and
$1\leqslant i_{1}\lt i_{2}\leqslant s$
and
![]() $j_{1},j_{2}\in [t]$
,
$j_{1},j_{2}\in [t]$
,
Moreover, for a pair of vertices
![]() $a_{i}^{(j_{1})}$
and
$a_{i}^{(j_{1})}$
and
![]() $a_{i}^{(j_{2})}$
with
$a_{i}^{(j_{2})}$
with
![]() $j_1\neq j_2$
,
$j_1\neq j_2$
,
![]() $a_{i}^{(j_{1})}a_{i}^{(j_{2})}\in E(G)$
implies
$a_{i}^{(j_{1})}a_{i}^{(j_{2})}\in E(G)$
implies
![]() $|a_{i}^{(j_{1})}-a_{i}^{(j_{2})}|\geqslant 2-\mu$
. Note that for any vertex
$|a_{i}^{(j_{1})}-a_{i}^{(j_{2})}|\geqslant 2-\mu$
. Note that for any vertex
![]() $v\in V_i$
, its neighbours in
$v\in V_i$
, its neighbours in
![]() $V_i$
all lie in a spherical cap
$V_i$
all lie in a spherical cap
![]() $C$
whose points are within distance
$C$
whose points are within distance
![]() $d=d_0\pm \mu /4$
from its centre, where
$d=d_0\pm \mu /4$
from its centre, where
![]() $d_0^2=4\mu -\mu ^2$
. As the height of such a cap is
$d_0^2=4\mu -\mu ^2$
. As the height of such a cap is
![]() $d^2/2\leqslant 4\mu$
. Thus by Lemma 2.7, the measure of
$d^2/2\leqslant 4\mu$
. Thus by Lemma 2.7, the measure of
![]() $C$
is at most
$C$
is at most
![]() $e^{-h(1-4\mu )^2/2}$
. Consequently,
$e^{-h(1-4\mu )^2/2}$
. Consequently,
Therefore, the probability that the selected vertices forming a copy of
![]() ${{{k^2}} \over 4}$
-clique is positive, then the claim follows.
${{{k^2}} \over 4}$
-clique is positive, then the claim follows.
Therefore with positive probability, the random graph
![]() $G$
has positive
$G$
has positive
![]() ${K_{{{{k^2}} \over 4}}}$
-density. This completes the proof of Theorem 1.4.
${K_{{{{k^2}} \over 4}}}$
-density. This completes the proof of Theorem 1.4.
5. Results in posets
5.1. Incomparability graphs
We first show how Theorem 1.7 implies Theorem 1.6, which we restate for convenience.
Theorem 1.6.
Let
![]() $c \in (0,{1 \over 2})$
,
$c \in (0,{1 \over 2})$
,
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $n$
be sufficiently large. If
$n$
be sufficiently large. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex incomparability graph with
$n$
-vertex incomparability graph with
![]() $\varrho _k(G)\geqslant c$
, then
$\varrho _k(G)\geqslant c$
, then
![]() $G$
contains a
$G$
contains a
![]() ${K_k}[{{{c^4}n} \over {{{10}^8}{k^2}\log n}}]$
.
${K_k}[{{{c^4}n} \over {{{10}^8}{k^2}\log n}}]$
.
Proof of Theorem
1.6. Let
![]() $G$
be an incomparability graph on
$G$
be an incomparability graph on
![]() $n$
vertices with at least
$n$
vertices with at least
![]() $cn^k$
$cn^k$
![]() $k$
-cliques and for the sake of contradiction, suppose
$k$
-cliques and for the sake of contradiction, suppose
![]() $G$
does not contain any copy of
$G$
does not contain any copy of
![]() $K_k[q],$
where
$K_k[q],$
where
![]() $q = {{{c^4}n} \over {{{10}^8}{k^2}\log n}}.$
Let
$q = {{{c^4}n} \over {{{10}^8}{k^2}\log n}}.$
Let
![]() $\varepsilon = {c \over 4}$
and apply Theorem 1.7 to obtain a partition
$\varepsilon = {c \over 4}$
and apply Theorem 1.7 to obtain a partition
![]() $V(G) = V_0 \sqcup V_1 \sqcup \cdots \sqcup V_m$
. Note that
$V(G) = V_0 \sqcup V_1 \sqcup \cdots \sqcup V_m$
. Note that
![]() ${n \over m} \geqslant t = {{{\varepsilon ^7}n} \over {{{10}^{11}}{k^5}}} \geqslant q$
when
${n \over m} \geqslant t = {{{\varepsilon ^7}n} \over {{{10}^{11}}{k^5}}} \geqslant q$
when
![]() $n$
is sufficiently large. We then consider
$n$
is sufficiently large. We then consider
![]() $k$
-cliques in
$k$
-cliques in
![]() $G$
and list three possible cases as follows.
$G$
and list three possible cases as follows.
-
1. There are at most
 $|V_0| n^{k-1} \leqslant \varepsilon n^k$
$|V_0| n^{k-1} \leqslant \varepsilon n^k$
 $k$
-cliques containing at least one vertex in
$k$
-cliques containing at least one vertex in
 $V_{0}$
.
$V_{0}$
. -
2. The number of
 $k$
-cliques in
$k$
-cliques in
 $G$
such that there are at least two vertices in the same part is at most
$G$
such that there are at least two vertices in the same part is at most
 $m t^2 n^{k-2} \leqslant t n^{k-1} \leqslant \varepsilon n^k$
.
$m t^2 n^{k-2} \leqslant t n^{k-1} \leqslant \varepsilon n^k$
. -
3. For each
 $k$
-clique with all vertices belonging to distinct parts
$k$
-clique with all vertices belonging to distinct parts
 $V_{i_{1}},V_{i_{2}},\ldots ,V_{i_{k}}$
, note that at least one pair of these parts is inhomogeneous, for otherwise there is a copy of
$V_{i_{1}},V_{i_{2}},\ldots ,V_{i_{k}}$
, note that at least one pair of these parts is inhomogeneous, for otherwise there is a copy of
 $K_k[t]$
and thus
$K_k[t]$
and thus
 $K_k[q]$
in
$K_k[q]$
in
 $G$
. Since there are at most
$G$
. Since there are at most
 $\varepsilon m^2$
inhomogeneous pairs, the number of
$\varepsilon m^2$
inhomogeneous pairs, the number of
 $k$
-cliques in
$k$
-cliques in
 $G$
with all vertices in distinct parts among
$G$
with all vertices in distinct parts among
 $V_1, \ldots , V_m$
is at most
$V_1, \ldots , V_m$
is at most
 $\varepsilon m^2 t^2 n^{k-2} \leqslant \varepsilon n^k$
.
$\varepsilon m^2 t^2 n^{k-2} \leqslant \varepsilon n^k$
.
Therefore,
![]() $G$
contains at most
$G$
contains at most
![]() $3 \varepsilon n^k \lt c n^k$
$3 \varepsilon n^k \lt c n^k$
![]() $k$
-cliques, which is a contradiction to our assumption.
$k$
-cliques, which is a contradiction to our assumption.
We proceed to the proof of Theorem 1.7.
Proof of Theorem
1.7. Let
![]() $(P,\prec )$
be a partially ordered set on
$(P,\prec )$
be a partially ordered set on
![]() $n$
elements such that
$n$
elements such that
![]() $G$
is the incomparability graph of
$G$
is the incomparability graph of
![]() $P$
. Let
$P$
. Let
![]() $\lt '$
be an arbitrary linear extension of
$\lt '$
be an arbitrary linear extension of
![]() $\prec$
, and let
$\prec$
, and let
![]() $x_1\lt 'x_{2}\lt'$
$x_1\lt 'x_{2}\lt'$
![]() $\cdots \lt 'x_{n}$
be the enumeration of the elements of
$\cdots \lt 'x_{n}$
be the enumeration of the elements of
![]() $G$
by
$G$
by
![]() $\lt '$
. Let
$\lt '$
. Let
![]() $s = {{10} \over \varepsilon }$
and
$s = {{10} \over \varepsilon }$
and
![]() $\ell = {{10k} \over \varepsilon }.$
We equally partition
$\ell = {{10k} \over \varepsilon }.$
We equally partition
![]() $P$
into
$P$
into
![]() $s$
intervals
$s$
intervals
![]() $P_1,\ldots , P_s$
, where
$P_1,\ldots , P_s$
, where
![]() ${P_i} = \{ {x_{{{(i - 1)n} \over s} + 1}}, \ldots ,{x_{{{in} \over s}}}\} $
for each
${P_i} = \{ {x_{{{(i - 1)n} \over s} + 1}}, \ldots ,{x_{{{in} \over s}}}\} $
for each
![]() $1\leqslant i\leqslant s$
.
$1\leqslant i\leqslant s$
.
Claim 5.1.
Every subset of
![]() $P$
of size
$P$
of size
![]() ${{\varepsilon n} \over {2s}}$
contains
${{\varepsilon n} \over {2s}}$
contains
![]() $\ell$
disjoint sets
$\ell$
disjoint sets
![]() $A_1,A_2,\ldots ,A_\ell$
satisfying
$A_1,A_2,\ldots ,A_\ell$
satisfying
![]() $A_1\succ A_2\succ \cdots \succ A_{\ell }$
and
$A_1\succ A_2\succ \cdots \succ A_{\ell }$
and
![]() $|A_i| = t$
for
$|A_i| = t$
for
![]() $1\leqslant i\leqslant \ell$
.
$1\leqslant i\leqslant \ell$
.
Proof of claim. Let
![]() $S$
be an arbitrary subset of
$S$
be an arbitrary subset of
![]() $P$
of size
$P$
of size
![]() ${{\varepsilon n} \over {2s}}$
and apply Lemma 2.4 to the subposet of
${{\varepsilon n} \over {2s}}$
and apply Lemma 2.4 to the subposet of
![]() $P$
induced on
$P$
induced on
![]() $S.$
If the former conclusion of Lemma 2.4 holds, we obtain
$S.$
If the former conclusion of Lemma 2.4 holds, we obtain
![]() $\ell$
sets
$\ell$
sets
![]() $A_1 \succ A_2 \succ \dots \succ A_\ell$
, each of size
$A_1 \succ A_2 \succ \dots \succ A_\ell$
, each of size
![]() ${{|S|} \over {{{10}^4}{\ell ^5}}} \geqslant {{{\varepsilon ^7}n} \over {{{10}^{11}}{k^5}}} = t$
as needed. If the latter conclusion of Lemma 2.4 holds, there are
${{|S|} \over {{{10}^4}{\ell ^5}}} \geqslant {{{\varepsilon ^7}n} \over {{{10}^{11}}{k^5}}} = t$
as needed. If the latter conclusion of Lemma 2.4 holds, there are
![]() $\ell$
pairwise incomparable sets in
$\ell$
pairwise incomparable sets in
![]() $P$
, each of size
$P$
, each of size
![]() ${{|S|} \over {40{\ell ^2}\log |S|}}\gt {{{\varepsilon ^4}n} \over {{{10}^5}{k^2}\log n}} = q$
. This implies the existence of
${{|S|} \over {40{\ell ^2}\log |S|}}\gt {{{\varepsilon ^4}n} \over {{{10}^5}{k^2}\log n}} = q$
. This implies the existence of
![]() $K_k[q]$
in
$K_k[q]$
in
![]() $G,$
contradicting our assumption and finishing the proof of the claim.
$G,$
contradicting our assumption and finishing the proof of the claim.
Let
![]() ${m_0} = \lfloor {{{(1 - \varepsilon )n} \over {st\ell }}} \rfloor .$
Then, for each
${m_0} = \lfloor {{{(1 - \varepsilon )n} \over {st\ell }}} \rfloor .$
Then, for each
![]() $i \in [s],$
iteratively using Claim 5.1, we can find
$i \in [s],$
iteratively using Claim 5.1, we can find
![]() $\ell m_0$
disjoint sets
$\ell m_0$
disjoint sets
![]() $\{B_{ij}^u\}_{j \in [m_0], u \in [\ell ]}$
in
$\{B_{ij}^u\}_{j \in [m_0], u \in [\ell ]}$
in
![]() $P_{i}$
, such that
$P_{i}$
, such that
![]() $|B_{ij}^u|=t$
and
$|B_{ij}^u|=t$
and
![]() $B_{ij}^1 \prec B_{ij}^2 \prec \dots \prec B_{ij}^\ell$
for all
$B_{ij}^1 \prec B_{ij}^2 \prec \dots \prec B_{ij}^\ell$
for all
![]() $i \in [s], j \in [m_0].$
Let
$i \in [s], j \in [m_0].$
Let
![]() $V_0 = P {\setminus} \bigcup _{i \in [s], j \in [m_0], u \in [\ell ]} B_{ij}^u$
and
$V_0 = P {\setminus} \bigcup _{i \in [s], j \in [m_0], u \in [\ell ]} B_{ij}^u$
and
![]() $m = s m_0 \ell$
, and we identify
$m = s m_0 \ell$
, and we identify
![]() $V_1, \dots , V_m$
with the sets
$V_1, \dots , V_m$
with the sets
![]() $\{B_{ij}^u\}_{i \in [s], j \in [m_0], u \in [\ell ]}$
. Note that
$\{B_{ij}^u\}_{i \in [s], j \in [m_0], u \in [\ell ]}$
. Note that
![]() $|V_0| = n - s m_0 \ell t \leqslant \varepsilon n$
as needed. It remains to verify that at most
$|V_0| = n - s m_0 \ell t \leqslant \varepsilon n$
as needed. It remains to verify that at most
![]() $\varepsilon m^2$
pairs
$\varepsilon m^2$
pairs
![]() $(V_i, V_j)$
are inhomogeneous in
$(V_i, V_j)$
are inhomogeneous in
![]() $G,$
that is, there are at most
$G,$
that is, there are at most
![]() $\varepsilon m^2$
pairs
$\varepsilon m^2$
pairs
![]() $((i, j, u), (i', j', u'))$
such that neither
$((i, j, u), (i', j', u'))$
such that neither
![]() $B_{ij}^u \prec B_{i'j'}^{u'}$
, nor
$B_{ij}^u \prec B_{i'j'}^{u'}$
, nor
![]() $B_{i'j'}^{u'} \prec B_{ij}^u$
, nor
$B_{i'j'}^{u'} \prec B_{ij}^u$
, nor
![]() $B_{ij}^u$
and
$B_{ij}^u$
and
![]() $B_{i'j'}^{u'}$
are incomparable.
$B_{i'j'}^{u'}$
are incomparable.
Observe that the number of pairs
![]() $((i, j, u), (i', j', u'))$
with
$((i, j, u), (i', j', u'))$
with
![]() $i = i'$
is at most
$i = i'$
is at most
![]() $s{({m_0}\ell )^2} = {{{m^2}} \over s} = {{\varepsilon {m^2}} \over {10}}$
. To upper bound the number of inhomogeneous pairs coming from different sets
$s{({m_0}\ell )^2} = {{{m^2}} \over s} = {{\varepsilon {m^2}} \over {10}}$
. To upper bound the number of inhomogeneous pairs coming from different sets
![]() $P_i,P_{i'}$
, we shall need the following claim.
$P_i,P_{i'}$
, we shall need the following claim.
Claim 5.2.
For fixed pairs
![]() $(i,j), (i',j')$
with
$(i,j), (i',j')$
with
![]() $i \lt i'$
, the number of pairs
$i \lt i'$
, the number of pairs
![]() $(u, u') \in [\ell ]^2$
such that
$(u, u') \in [\ell ]^2$
such that
![]() $(B_{ij}^u, B_{i'j'}^{u'})$
is inhomogeneous is at most
$(B_{ij}^u, B_{i'j'}^{u'})$
is inhomogeneous is at most
![]() $2 \ell - 1.$
$2 \ell - 1.$
Before proving the claim, we finish the proof of the lemma. The number of inhomogeneous pairs coming from different sets
![]() $P_i,P_{i'}$
is at most
$P_i,P_{i'}$
is at most
![]() ${s^2}m_0^2(2\ell - 1){{2{m^2}} \over \ell }\lt {{\varepsilon {m^2}} \over 5}$
. Thus the total number of inhomogeneous pairs is at most
${s^2}m_0^2(2\ell - 1){{2{m^2}} \over \ell }\lt {{\varepsilon {m^2}} \over 5}$
. Thus the total number of inhomogeneous pairs is at most
![]() $\varepsilon m^2,$
as required.
$\varepsilon m^2,$
as required.
We are left to prove Claim 5.2. Let
![]() $Z$
denote the set of pairs
$Z$
denote the set of pairs
![]() $(u, u') \in [\ell ]^2$
such that
$(u, u') \in [\ell ]^2$
such that
![]() $(B_{ij}^u, B_{i'j'}^{u'})$
is inhomogeneous. We will show that for any distinct pairs
$(B_{ij}^u, B_{i'j'}^{u'})$
is inhomogeneous. We will show that for any distinct pairs
![]() $(u, u'), (v, v') \in Z$
, it holds that
$(u, u'), (v, v') \in Z$
, it holds that
Indeed, this would prove the claim since trivially
![]() $u + u' \in [2, 2\ell ]$
for any
$u + u' \in [2, 2\ell ]$
for any
![]() $(u, u') \in Z$
.
$(u, u') \in Z$
.
Consider two distinct pairs
![]() $(u, u'), (v, v') \in Z$
and suppose that
$(u, u'), (v, v') \in Z$
and suppose that
![]() $u + u' = v + v'$
. Without loss of generality, assume that
$u + u' = v + v'$
. Without loss of generality, assume that
![]() $u \lt v$
which then implies
$u \lt v$
which then implies
![]() $v' \lt u'.$
Since
$v' \lt u'.$
Since
![]() $u \lt v,$
it follows that
$u \lt v,$
it follows that
![]() $B_{ij}^u \prec B_{ij}^v.$
Because the pair
$B_{ij}^u \prec B_{ij}^v.$
Because the pair
![]() $(B_{ij}^v, B_{i'j'}^{v'})$
is not incomparable, there exist some
$(B_{ij}^v, B_{i'j'}^{v'})$
is not incomparable, there exist some
![]() $x \in B_{ij}^v, y \in B_{i'j'}^{v'}$
which are comparable in
$x \in B_{ij}^v, y \in B_{i'j'}^{v'}$
which are comparable in
![]() $P.$
Since
$P.$
Since
![]() $i \lt i', x \in P_i, y \in P_{i'}$
and
$i \lt i', x \in P_i, y \in P_{i'}$
and
![]() $x \lt ' y$
by the assumed linear ordering, it follows that
$x \lt ' y$
by the assumed linear ordering, it follows that
![]() $x \prec y.$
Finally, since
$x \prec y.$
Finally, since
![]() $v' \lt u',$
we have
$v' \lt u',$
we have
![]() $y \prec B_{i'j'}^{u'}$
and by transitivity it follows that
$y \prec B_{i'j'}^{u'}$
and by transitivity it follows that
![]() $B_{ij}^u \prec x \prec y \prec B_{i'j'}^{u'}$
(see Fig. 3), contradicting our assumption that
$B_{ij}^u \prec x \prec y \prec B_{i'j'}^{u'}$
(see Fig. 3), contradicting our assumption that
![]() $(u, u') \in Z.$
$(u, u') \in Z.$

Figure 3. Claim 5.2: arrows in the curves indicate the order in
![]() $P$
.
$P$
.
Remark 5.3. The dimension of a poset
![]() $P$
is the least integer
$P$
is the least integer
![]() $d$
for which there exist linear extensions
$d$
for which there exist linear extensions
![]() $L_1,\dots ,L_d$
whose intersection equals
$L_1,\dots ,L_d$
whose intersection equals
![]() $P$
. If
$P$
. If
![]() $G$
is the incomparability graph of a poset of dimension at most
$G$
is the incomparability graph of a poset of dimension at most
![]() $d$
, then replacing Lemma 2.4 in the proof of Theorems 1.7 and 1.6 by Theorem 2.3 of Suk–Zeng [Reference Suk and Zeng30] yields a linear blowup parameter; in particular, we may take
$d$
, then replacing Lemma 2.4 in the proof of Theorems 1.7 and 1.6 by Theorem 2.3 of Suk–Zeng [Reference Suk and Zeng30] yields a linear blowup parameter; in particular, we may take
![]() $q=\Omega _{k,d}(n)$
, and the remainder of the argument goes through without further modification.
$q=\Omega _{k,d}(n)$
, and the remainder of the argument goes through without further modification.
5.2.
 $r$
-comparability graphs
$r$
-comparability graphs
In this subsection, we prove Theorem 1.8, which we restate here.
Theorem 1.8.
Let
![]() $r,h\in \mathbb{N}$
with
$r,h\in \mathbb{N}$
with
![]() $h\geqslant 2$
,
$h\geqslant 2$
,
![]() $k=(2h-2)^{r}+1$
and
$k=(2h-2)^{r}+1$
and
![]() $\varepsilon \gt 0$
. Let
$\varepsilon \gt 0$
. Let
![]() $G=\bigcup _{i\in [r]}G({\prec}_{i})$
be an
$G=\bigcup _{i\in [r]}G({\prec}_{i})$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $r$
-comparability graph. If
$r$
-comparability graph. If
![]() $\varrho _k(G)\geqslant \varepsilon$
, then some
$\varrho _k(G)\geqslant \varepsilon$
, then some
![]() $G({\prec}_{i})$
,
$G({\prec}_{i})$
,
![]() $i\in [r]$
, contains a copy of
$i\in [r]$
, contains a copy of
![]() ${K_h}[{{\varepsilon n} \over r}]$
.
${K_h}[{{\varepsilon n} \over r}]$
.
Proof. First we prove the case
![]() $r=1$
. For two elements
$r=1$
. For two elements
![]() $x,y$
, we write
$x,y$
, we write
![]() $x\prec y$
if
$x\prec y$
if
![]() $x\prec _i y$
for every
$x\prec _i y$
for every
![]() $i\in [r]$
. For a copy of
$i\in [r]$
. For a copy of
![]() $K_{2h-1}$
in
$K_{2h-1}$
in
![]() $G$
with vertex set
$G$
with vertex set
![]() $\{x_{1},x_{2},\ldots ,x_{2h-1}\}$
, we can assume the order is
$\{x_{1},x_{2},\ldots ,x_{2h-1}\}$
, we can assume the order is
![]() $x_{1}\prec x_{2}\prec \cdots \prec x_{2h-1}$
. By the pigeonhole principle, there exists an
$x_{1}\prec x_{2}\prec \cdots \prec x_{2h-1}$
. By the pigeonhole principle, there exists an
![]() $(h-1)$
-tuple
$(h-1)$
-tuple
![]() $(x_2,x_4,\ldots ,x_{2h-2})$
in
$(x_2,x_4,\ldots ,x_{2h-2})$
in
![]() $G$
such that there are at least
$G$
such that there are at least
![]() $\varepsilon n^{h}$
choices of
$\varepsilon n^{h}$
choices of
![]() $h$
-tuples
$h$
-tuples
![]() $(x_1,x_3,\ldots ,x_{2h-1})$
where
$(x_1,x_3,\ldots ,x_{2h-1})$
where
![]() $x_{1}x_{2}\cdots x_{2h-1}$
together form a copy of
$x_{1}x_{2}\cdots x_{2h-1}$
together form a copy of
![]() $K_{2h-1}$
. Fix such an
$K_{2h-1}$
. Fix such an
![]() $(h-1)$
-tuple
$(h-1)$
-tuple
![]() $(x_{2},x_{4},\ldots ,x_{2h-2})$
, let
$(x_{2},x_{4},\ldots ,x_{2h-2})$
, let
![]() $D_{1}\,:\!=\,\{x|x\prec x_2\}$
,
$D_{1}\,:\!=\,\{x|x\prec x_2\}$
,
![]() $D_{h}\,:\!=\,\{x|x_{2h-2}\prec x\}$
, and
$D_{h}\,:\!=\,\{x|x_{2h-2}\prec x\}$
, and
![]() $D_{i}\,:\!=\,\{x|x_{2i-2}\prec x\prec x_{2i}$
} for any
$D_{i}\,:\!=\,\{x|x_{2i-2}\prec x\prec x_{2i}$
} for any
![]() $2\leqslant i\leqslant h-1$
. Note that if
$2\leqslant i\leqslant h-1$
. Note that if
![]() $x_1 \cdots x_{2h-1}$
form a copy of
$x_1 \cdots x_{2h-1}$
form a copy of
![]() $K_{2h-1}$
, then
$K_{2h-1}$
, then
![]() $x_{2i-1}\in D_i$
by our above assumption, which also yields that
$x_{2i-1}\in D_i$
by our above assumption, which also yields that
![]() $\prod _{i=1}^h|D_i|\geqslant \varepsilon n^{h}$
. Obviously,
$\prod _{i=1}^h|D_i|\geqslant \varepsilon n^{h}$
. Obviously,
![]() $|D_{i}|\leqslant n$
, therefore
$|D_{i}|\leqslant n$
, therefore
![]() $|D_i|\geqslant \varepsilon n$
holds for all
$|D_i|\geqslant \varepsilon n$
holds for all
![]() $1\leqslant i\leqslant h$
. Moreover, for each
$1\leqslant i\leqslant h$
. Moreover, for each
![]() $1\leqslant i\lt j\leqslant h$
and for any pair of vertices
$1\leqslant i\lt j\leqslant h$
and for any pair of vertices
![]() $a\in D_{i}, b\in D_{j}$
, we have
$a\in D_{i}, b\in D_{j}$
, we have
![]() $a\prec x_{2i}\prec b$
, therefore
$a\prec x_{2i}\prec b$
, therefore
![]() $G[\bigcup _{i=1}^{h}D_{i}]$
contains a copy of
$G[\bigcup _{i=1}^{h}D_{i}]$
contains a copy of
![]() $K_{h}[\varepsilon n]$
.
$K_{h}[\varepsilon n]$
.
Next we proceed to the proof of the general cases
![]() $r\geqslant 2$
. Let
$r\geqslant 2$
. Let
![]() $K$
be an arbitrary
$K$
be an arbitrary
![]() $k$
-clique in
$k$
-clique in
![]() $G$
. For each vertex
$G$
. For each vertex
![]() $x\in V(K)$
, let
$x\in V(K)$
, let
![]() $p_i(x)$
be the maximum number
$p_i(x)$
be the maximum number
![]() $t$
such that there is a chain of the form
$t$
such that there is a chain of the form
![]() $x=a_{1}\prec _{i}a_{2}\prec _{i}a_{3}\prec _{i}\cdots \prec _{i}a_{t}$
, where
$x=a_{1}\prec _{i}a_{2}\prec _{i}a_{3}\prec _{i}\cdots \prec _{i}a_{t}$
, where
![]() $a_{1},a_{2},\ldots ,a_{t}$
are in
$a_{1},a_{2},\ldots ,a_{t}$
are in
![]() $V(K)$
. Denote
$V(K)$
. Denote
![]() $p(x) = (p_1(x), \dots , p_r(x)).$
We first prove the following claim.
$p(x) = (p_1(x), \dots , p_r(x)).$
We first prove the following claim.
Claim 5.4.
For a given
![]() $k$
-clique
$k$
-clique
![]() $K$
and any distinct
$K$
and any distinct
![]() $x,y\in V(K)$
, we have
$x,y\in V(K)$
, we have
![]() $p(x) \neq p(y).$
$p(x) \neq p(y).$
Proof of claim. As
![]() $x$
and
$x$
and
![]() $y$
are adjacent in
$y$
are adjacent in
![]() $G$
, they are comparable in one of the partial orders. Without loss of generality, assume that
$G$
, they are comparable in one of the partial orders. Without loss of generality, assume that
![]() $x\prec _{1} y$
. By definition of
$x\prec _{1} y$
. By definition of
![]() $p_{i}(y)$
, we can find a chain of the form
$p_{i}(y)$
, we can find a chain of the form
![]() $y=a_{1}\prec _{1}a_{2}\prec _{1}\cdots \prec _{1}a_{p_{1}(y)}$
, such that all the elements
$y=a_{1}\prec _{1}a_{2}\prec _{1}\cdots \prec _{1}a_{p_{1}(y)}$
, such that all the elements
![]() $a_{2},a_{3},\ldots ,a_{p_{1}(y)}$
are in
$a_{2},a_{3},\ldots ,a_{p_{1}(y)}$
are in
![]() $V(K)$
. However, then we have
$V(K)$
. However, then we have
![]() $x\prec _{1}y\prec _{1}a_{2}\cdots \prec _{1}a_{p_1(y)}$
, which implies that
$x\prec _{1}y\prec _{1}a_{2}\cdots \prec _{1}a_{p_1(y)}$
, which implies that
![]() $p_1(x)\gt p_1(y)$
. Therefore,
$p_1(x)\gt p_1(y)$
. Therefore,
![]() $p(x) \neq p(y)$
.
$p(x) \neq p(y)$
.
Let
![]() $G_{i}=G({\prec}_i)$
be the comparability graph of
$G_{i}=G({\prec}_i)$
be the comparability graph of
![]() $\prec _{i}$
. For each
$\prec _{i}$
. For each
![]() $k$
-clique
$k$
-clique
![]() $K$
in
$K$
in
![]() $G$
, by definition we have
$G$
, by definition we have
![]() $p_i(x) \geqslant 1,$
for all
$p_i(x) \geqslant 1,$
for all
![]() $x \in V(K), i \in [r]$
. By Claim 5.4, since
$x \in V(K), i \in [r]$
. By Claim 5.4, since
![]() $k \gt (2h-2)^r,$
there must exist
$k \gt (2h-2)^r,$
there must exist
![]() $x \in V(K)$
and
$x \in V(K)$
and
![]() $i \in [r]$
such that
$i \in [r]$
such that
![]() $p_i(x) \geqslant 2h-1$
. In particular, this implies that
$p_i(x) \geqslant 2h-1$
. In particular, this implies that
![]() $G_i$
contains a
$G_i$
contains a
![]() $(2h-1)$
-clique inside
$(2h-1)$
-clique inside
![]() $K$
. By the pigeonhole principle again, there exists some index
$K$
. By the pigeonhole principle again, there exists some index
![]() $j\in [r]$
such that for at least
$j\in [r]$
such that for at least
![]() ${{\varepsilon {n^k}} \over r}$
many
${{\varepsilon {n^k}} \over r}$
many
![]() $k$
-cliques
$k$
-cliques
![]() $K$
in
$K$
in
![]() $G$
, there is a
$G$
, there is a
![]() $(2h-1)$
-clique in
$(2h-1)$
-clique in
![]() $G_j$
inside
$G_j$
inside
![]() $K$
. On the other hand, each
$K$
. On the other hand, each
![]() $(2h-1)$
-clique in
$(2h-1)$
-clique in
![]() $G_j$
can be contained in at most
$G_j$
can be contained in at most
![]() $n^{k-(2h-1)}$
many
$n^{k-(2h-1)}$
many
![]() $k$
-cliques in
$k$
-cliques in
![]() $G$
, which yields that totally there are at least
$G$
, which yields that totally there are at least
![]() ${{\varepsilon {n^{2h - 1}}} \over r}$
many cliques of size
${{\varepsilon {n^{2h - 1}}} \over r}$
many cliques of size
![]() $2h-1$
in
$2h-1$
in
![]() $G_{j}$
. Applying the result in the case
$G_{j}$
. Applying the result in the case
![]() $r=1,$
we obtain a copy of
$r=1,$
we obtain a copy of
![]() ${K_h}[{{\varepsilon n} \over r}]$
in
${K_h}[{{\varepsilon n} \over r}]$
in
![]() $G_{j}$
.
$G_{j}$
.
6. Hereditary graphs and
 $B_k$
property
$B_k$
property
6.1.
 $B_2$
property implies
$B_2$
property implies
 $B_k$
property in hereditary graphs
$B_k$
property in hereditary graphs
Proof of Theorem
1.9. Assume that
![]() $\mathcal{G}$
is a hereditary family which has the
$\mathcal{G}$
is a hereditary family which has the
![]() $B_2$
property with function
$B_2$
property with function
![]() $f$
. For any
$f$
. For any
![]() $\varepsilon \gt 0$
, we set a function
$\varepsilon \gt 0$
, we set a function
We will show that
![]() $\mathcal{G}$
has the
$\mathcal{G}$
has the
![]() $B_k$
property with respect to the function
$B_k$
property with respect to the function
![]() $h$
.
$h$
.
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph in the family
$n$
-vertex graph in the family
![]() $\mathcal{G}$
such that
$\mathcal{G}$
such that
![]() $G$
has at least
$G$
has at least
![]() $\varepsilon n^k$
$\varepsilon n^k$
![]() $k$
-cliques. Let
$k$
-cliques. Let
![]() $m = {4 \over \varepsilon }$
. If
$m = {4 \over \varepsilon }$
. If
![]() $n\leqslant m$
, then we are done by Nikiforov’s result [Reference Nikiforov27]. Otherwise, by Lemma 2.1, there exists
$n\leqslant m$
, then we are done by Nikiforov’s result [Reference Nikiforov27]. Otherwise, by Lemma 2.1, there exists
![]() $M=M(m,\varepsilon _0)$
such that
$M=M(m,\varepsilon _0)$
such that
![]() $V(G)$
admits an
$V(G)$
admits an
![]() $\varepsilon$
-regular equitable partition
$\varepsilon$
-regular equitable partition
![]() $\mathcal{P}$
with
$\mathcal{P}$
with
![]() $K+1$
parts
$K+1$
parts
![]() $V_{0},V_{1},\ldots ,V_{K}$
, where
$V_{0},V_{1},\ldots ,V_{K}$
, where
![]() $m \leqslant K \leqslant M$
. Setting
$m \leqslant K \leqslant M$
. Setting
![]() $|V_1|=q$
, we can see that
$|V_1|=q$
, we can see that
![]() $(1 - {\varepsilon _0}){n \over K}\leqslant q\leqslant {n \over m}$
.
$(1 - {\varepsilon _0}){n \over K}\leqslant q\leqslant {n \over m}$
.
We then construct an auxiliary graph
![]() $G'$
with vertex set
$G'$
with vertex set
![]() $\{V_{1},V_{2},\ldots ,V_{K}\}$
, and a pair of vertices
$\{V_{1},V_{2},\ldots ,V_{K}\}$
, and a pair of vertices
![]() $V_{i},V_{j}$
is adjacent in
$V_{i},V_{j}$
is adjacent in
![]() $G'$
if and only if
$G'$
if and only if
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $\varepsilon _0$
-regular and
$\varepsilon _0$
-regular and
![]() $d({V_i},{V_j})\gt {\varepsilon \over 2}$
.
$d({V_i},{V_j})\gt {\varepsilon \over 2}$
.
Claim 6.1.
![]() $G'$
contains a
$G'$
contains a
![]() $k$
-clique.
$k$
-clique.
Proof of claim. Suppose that
![]() $G'$
is
$G'$
is
![]() $K_{k}$
-free, then for any
$K_{k}$
-free, then for any
![]() $k$
-clique in
$k$
-clique in
![]() $G$
with vertex set
$G$
with vertex set
![]() $\{v_1,v_2,\cdots ,v_k\}$
, at least one of the following four types occurs:
$\{v_1,v_2,\cdots ,v_k\}$
, at least one of the following four types occurs:
-
• At least one of the vertices
 $v_1,v_2,\ldots ,v_k$
belongs to
$v_1,v_2,\ldots ,v_k$
belongs to
 $V_0$
. Note that
$V_0$
. Note that
 $|V_0|\leqslant \varepsilon _0 n$
, the number of
$|V_0|\leqslant \varepsilon _0 n$
, the number of
 $k$
-tuples of this type is at most
$k$
-tuples of this type is at most
 $\varepsilon _0 n^k$
.
$\varepsilon _0 n^k$
. -
• At least two of the vertices
 $v_1,v_2,\ldots ,v_k$
belong to some
$v_1,v_2,\ldots ,v_k$
belong to some
 $V_{i}$
, where
$V_{i}$
, where
 $i\in [K]$
. Note that
$i\in [K]$
. Note that
 $|{V_i}|{n \over m}$
, the number of the tuples of this type is at most
$|{V_i}|{n \over m}$
, the number of the tuples of this type is at most
 ${{{n^k}} \over m} \leqslant {\varepsilon \over 4}{n^k}$
.
${{{n^k}} \over m} \leqslant {\varepsilon \over 4}{n^k}$
. -
• There exist some
 $v_i\in V_a, v_j\in V_b$
such that
$v_i\in V_a, v_j\in V_b$
such that
 $V_a$
and
$V_a$
and
 $V_b$
are not
$V_b$
are not
 $\varepsilon _0$
-regular, where
$\varepsilon _0$
-regular, where
 $i,j\in [k]$
and
$i,j\in [k]$
and
 $a,b\in [K]$
. Note that there are at most
$a,b\in [K]$
. Note that there are at most
 $\varepsilon _0 K^{2}$
pairs
$\varepsilon _0 K^{2}$
pairs
 $(V_{i},V_{j})$
being not
$(V_{i},V_{j})$
being not
 $\varepsilon _0$
-regular, therefore the number of
$\varepsilon _0$
-regular, therefore the number of
 $k$
-tuples of this type is at most
$k$
-tuples of this type is at most
 $\varepsilon _0 n^k$
.
$\varepsilon _0 n^k$
. -
• There exist some
 $v_i\in V_a, v_j\in V_b$
such that
$v_i\in V_a, v_j\in V_b$
such that
 $d({V_a},{V_b})\lt {\varepsilon \over 2}$
, where
$d({V_a},{V_b})\lt {\varepsilon \over 2}$
, where
 $i,j\in [k]$
and
$i,j\in [k]$
and
 $a,b\in [K]$
. Then, for fixed
$a,b\in [K]$
. Then, for fixed
 $V_a,V_b$
, there are at most
$V_a,V_b$
, there are at most
 ${{\varepsilon {q^2}} \over 2}$
choices of
${{\varepsilon {q^2}} \over 2}$
choices of
 $v_i,v_j$
, hence the number of
$v_i,v_j$
, hence the number of
 $k$
-tuples of this type is at most
$k$
-tuples of this type is at most
 ${m^2} \cdot {{\varepsilon {q^2}} \over 2} \cdot {n^{k - 2}}\leqslant {{\varepsilon {n^k}} \over 2}$
.
${m^2} \cdot {{\varepsilon {q^2}} \over 2} \cdot {n^{k - 2}}\leqslant {{\varepsilon {n^k}} \over 2}$
.
Hence, the total number of
![]() $k$
-cliques in
$k$
-cliques in
![]() $G$
is less than
$G$
is less than
![]() $\varepsilon n^k$
, a contradiction.
$\varepsilon n^k$
, a contradiction.
Without loss of generality, we can assume that
![]() $V_{1},V_{2},\ldots ,V_{k}$
form a clique in
$V_{1},V_{2},\ldots ,V_{k}$
form a clique in
![]() $G'$
. We consider two cases depending on whether some
$G'$
. We consider two cases depending on whether some
![]() $V_i$
is locally dense.
$V_i$
is locally dense.
Case 1. At least one of the clusters
![]() $G[V_1],\ldots ,G[V_k]$
is
$G[V_1],\ldots ,G[V_k]$
is
![]() $(\varepsilon _1,\varepsilon _2)$
-dense. Without loss of generality, we assume that
$(\varepsilon _1,\varepsilon _2)$
-dense. Without loss of generality, we assume that
![]() $G[V_1]$
is
$G[V_1]$
is
![]() $(\varepsilon _1,\varepsilon _2)$
-dense. We will use induction to show that for
$(\varepsilon _1,\varepsilon _2)$
-dense. We will use induction to show that for
![]() $2\leqslant t\leqslant k$
, we can find a copy of
$2\leqslant t\leqslant k$
, we can find a copy of
![]() ${K_t}[f{({{{\varepsilon _2}} \over 3})^{t - 1}}q]$
in
${K_t}[f{({{{\varepsilon _2}} \over 3})^{t - 1}}q]$
in
![]() $V_1$
. First, since
$V_1$
. First, since
![]() $G[V_1]$
has density at least
$G[V_1]$
has density at least
![]() $\varepsilon _2$
and
$\varepsilon _2$
and
![]() $B_2$
property, we can find a
$B_2$
property, we can find a
![]() ${K_2}[f({{{\varepsilon _2}} \over 3})q]$
in
${K_2}[f({{{\varepsilon _2}} \over 3})q]$
in
![]() $V_1$
. Suppose that we have found a copy of
$V_1$
. Suppose that we have found a copy of
![]() ${K_t}[f{({{{\varepsilon _2}} \over 3})^{t - 1}}q]$
in
${K_t}[f{({{{\varepsilon _2}} \over 3})^{t - 1}}q]$
in
![]() $V_1$
with parts
$V_1$
with parts
![]() $P_1,\ldots ,P_t$
. Since
$P_1,\ldots ,P_t$
. Since
![]() $G[V_1]$
is
$G[V_1]$
is
![]() $(\varepsilon _1,\varepsilon _2)$
-dense and
$(\varepsilon _1,\varepsilon _2)$
-dense and
![]() $\varepsilon _1\ll \varepsilon _2$
,
$\varepsilon _1\ll \varepsilon _2$
,
![]() $G[P_1]$
has density at least
$G[P_1]$
has density at least
![]() $\varepsilon _2$
, then we can find a copy of
$\varepsilon _2$
, then we can find a copy of
![]() ${K_2}[f({{{\varepsilon _2}} \over 3})|{P_1}|]$
in
${K_2}[f({{{\varepsilon _2}} \over 3})|{P_1}|]$
in
![]() $P_1$
. Thus, this biclique together with
$P_1$
. Thus, this biclique together with
![]() $P_2,\ldots ,P_t$
contains a copy of
$P_2,\ldots ,P_t$
contains a copy of
![]() ${K_{t + 1}}[f{({{{\varepsilon _2}} \over 3})^t}q]$
in
${K_{t + 1}}[f{({{{\varepsilon _2}} \over 3})^t}q]$
in
![]() $V_1$
. Taking
$V_1$
. Taking
![]() $t=k$
, we get the desired large blowup of
$t=k$
, we get the desired large blowup of
![]() $K_k$
.
$K_k$
.
Case 2. We may then assume that none of
![]() $G[V_1],\ldots ,G[V_k]$
is
$G[V_1],\ldots ,G[V_k]$
is
![]() $(\varepsilon _1,\varepsilon _2)$
-dense, then for each
$(\varepsilon _1,\varepsilon _2)$
-dense, then for each
![]() $i\in [k]$
, we can pick a subset
$i\in [k]$
, we can pick a subset
![]() $U_i' \subseteq V_i$
such that
$U_i' \subseteq V_i$
such that
![]() $|U_i'|\geqslant \varepsilon _1q$
and
$|U_i'|\geqslant \varepsilon _1q$
and
![]() $G[U_{i}']$
has density at most
$G[U_{i}']$
has density at most
![]() $\varepsilon _2$
. Let
$\varepsilon _2$
. Let
![]() $q_0=\lceil \varepsilon _1q\rceil$
. Pick a subset
$q_0=\lceil \varepsilon _1q\rceil$
. Pick a subset
![]() $U_i$
of
$U_i$
of
![]() $U_i'$
among all possible subgraphs with size
$U_i'$
among all possible subgraphs with size
![]() $q_0$
which achieve the minimal density, then
$q_0$
which achieve the minimal density, then
![]() $G[U_{i}]$
has density at most
$G[U_{i}]$
has density at most
![]() $\varepsilon _2$
. We will show that there is a copy of
$\varepsilon _2$
. We will show that there is a copy of
![]() $K_k[\delta n]$
such that the
$K_k[\delta n]$
such that the
![]() $i$
th-part is contained in
$i$
th-part is contained in
![]() $U_{i}$
.
$U_{i}$
.
Claim 6.2.
For any distinct subsets
![]() $A_i\subseteq U_i$
,
$A_i\subseteq U_i$
,
![]() $A_j\subseteq U_j$
, with
$A_j\subseteq U_j$
, with
![]() $i,j\in [k]$
and
$i,j\in [k]$
and
![]() $|A_i|=|A_j|\geqslant \varepsilon _{3}q_{0}$
, we can find subsets
$|A_i|=|A_j|\geqslant \varepsilon _{3}q_{0}$
, we can find subsets
![]() $B_i\subseteq A_i$
,
$B_i\subseteq A_i$
,
![]() $B_j\subseteq A_j$
with
$B_j\subseteq A_j$
with
![]() $|B_i|=|B_j|\geqslant \varepsilon _{4}|A_{i}|$
, such that
$|B_i|=|B_j|\geqslant \varepsilon _{4}|A_{i}|$
, such that
![]() $(B_i,B_j)$
forms a biclique.
$(B_i,B_j)$
forms a biclique.
Proof of claim. Since
![]() $U_i$
and
$U_i$
and
![]() $U_j$
are
$U_j$
are
![]() $\varepsilon _0$
-regular with density at least
$\varepsilon _0$
-regular with density at least
![]() $\varepsilon /2$
and
$\varepsilon /2$
and
![]() $|A_i|,|A_j|\geqslant \varepsilon _3q_0$
, we have
$|A_i|,|A_j|\geqslant \varepsilon _3q_0$
, we have
![]() $d({A_i},{A_j})\geqslant {\varepsilon \over 4}$
. Hence,
$d({A_i},{A_j})\geqslant {\varepsilon \over 4}$
. Hence,
![]() $G[A_i\cup A_j]$
has edge density at least
$G[A_i\cup A_j]$
has edge density at least
![]() ${\varepsilon \over {16}}$
since
${\varepsilon \over {16}}$
since
![]() $|A_i|=|A_j|$
. Thus by the
$|A_i|=|A_j|$
. Thus by the
![]() $B_{2}$
property, we can find a copy of
$B_{2}$
property, we can find a copy of
![]() ${K_2}[f({\varepsilon \over {16}})|{A_i}|]$
with parts
${K_2}[f({\varepsilon \over {16}})|{A_i}|]$
with parts
![]() $X,Y$
in
$X,Y$
in
![]() $G[A_i\cup A_j]$
.
$G[A_i\cup A_j]$
.
By symmetry, assume
![]() $|X \cap {A_i}|{{|X|}\geqslant \over 2}$
. Let
$|X \cap {A_i}|{{|X|}\geqslant \over 2}$
. Let
![]() $X_0=X\cap A_i$
. If
$X_0=X\cap A_i$
. If
![]() $|Y \cap {A_i}|\geqslant {{|Y|} \over 2}$
, letting
$|Y \cap {A_i}|\geqslant {{|Y|} \over 2}$
, letting
![]() $Y_0=Y\cap A_i$
, we have
$Y_0=Y\cap A_i$
, we have
 \begin{align*}{\varepsilon_{2}} \geqslant \frac{{e(G[{U_i}])}}{\left( \binom{|{U_i}|}{2}\right)} \geqslant \frac{{e({X_0},{Y_0})}}{|{U_i}{|^2}} \geqslant \frac{{|X||Y|}}{{4|{U_i}{|^2}}} \geqslant \frac{1}{4}\varepsilon_{3}^{2} f{\left(\frac{\varepsilon}{16} \right)^2},\end{align*}
\begin{align*}{\varepsilon_{2}} \geqslant \frac{{e(G[{U_i}])}}{\left( \binom{|{U_i}|}{2}\right)} \geqslant \frac{{e({X_0},{Y_0})}}{|{U_i}{|^2}} \geqslant \frac{{|X||Y|}}{{4|{U_i}{|^2}}} \geqslant \frac{1}{4}\varepsilon_{3}^{2} f{\left(\frac{\varepsilon}{16} \right)^2},\end{align*}
which is a contradiction. Therefore, we have
![]() $|Y \cap {A_j}| \geqslant {{|Y|} \over 2}$
. Let
$|Y \cap {A_j}| \geqslant {{|Y|} \over 2}$
. Let
![]() $Y_1=Y\cap A_j$
, then
$Y_1=Y\cap A_j$
, then
![]() $X_0,Y_1$
form a biclique. Finally, just pick
$X_0,Y_1$
form a biclique. Finally, just pick
![]() $B_i\subseteq X_0$
,
$B_i\subseteq X_0$
,
![]() $B_j\subseteq Y_1$
with
$B_j\subseteq Y_1$
with
![]() $|B_i|=|B_j|\geqslant \varepsilon _4|A_i|$
.
$|B_i|=|B_j|\geqslant \varepsilon _4|A_i|$
.
Claim 6.3.
For any subgraph
![]() $H$
of
$H$
of
![]() $K_k$
on vertex set
$K_k$
on vertex set
![]() $[k]$
, there are sets
$[k]$
, there are sets
![]() $W_{i} \subseteq U_i$
such that
$W_{i} \subseteq U_i$
such that
-
•
 $|W_1|=\cdots =|W_k|\geqslant \varepsilon _4^{e(H)}q_0$
; and
$|W_1|=\cdots =|W_k|\geqslant \varepsilon _4^{e(H)}q_0$
; and
-
• if
 $i$
and
$i$
and
 $j$
are adjacent in
$j$
are adjacent in
 $H$
, then
$H$
, then
 $(W_i,W_j)$
forms a biclique.
$(W_i,W_j)$
forms a biclique.
Proof of claim. We use induction on the number of edges in
![]() $H$
. When
$H$
. When
![]() $H$
is a empty graph, taking
$H$
is a empty graph, taking
![]() $W_i=U_i$
suffices.
$W_i=U_i$
suffices.
Assume we have proven the claim for
![]() $e(H) \leqslant s$
. When
$e(H) \leqslant s$
. When
![]() $e(H) = s+1$
, let
$e(H) = s+1$
, let
![]() $H'$
be the graph obtained by removing one edge
$H'$
be the graph obtained by removing one edge
![]() $e$
in
$e$
in
![]() $H$
. By symmetry, we may assume that
$H$
. By symmetry, we may assume that
![]() $e=\{1,2\}$
. By the induction hypothesis, we can find sets
$e=\{1,2\}$
. By the induction hypothesis, we can find sets
![]() $W'_{i} \subseteq U_i$
such that
$W'_{i} \subseteq U_i$
such that
-
•
 $|W'_1|=\cdots =|W'_k|\geqslant \varepsilon _4^{|H|-1}q_0$
; and
$|W'_1|=\cdots =|W'_k|\geqslant \varepsilon _4^{|H|-1}q_0$
; and -
• if
 $i$
and
$i$
and
 $j$
are adjacent in
$j$
are adjacent in
 $H'$
, then
$H'$
, then
 $(W'_i,W'_j)$
forms a biclique.
$(W'_i,W'_j)$
forms a biclique.
By Claim 6.2, we can find a subset
![]() $W_1$
of
$W_1$
of
![]() $W_1'$
, and subset
$W_1'$
, and subset
![]() $W_2$
of
$W_2$
of
![]() $W_2'$
with
$W_2'$
with
![]() $|W_1|=|W_2|\geqslant \varepsilon _4|W_1'|$
such that
$|W_1|=|W_2|\geqslant \varepsilon _4|W_1'|$
such that
![]() $(W_1,W_2)$
is a biclique. Finally, for
$(W_1,W_2)$
is a biclique. Finally, for
![]() $3\leqslant i\leqslant k$
, choose a subset
$3\leqslant i\leqslant k$
, choose a subset
![]() $W_i$
of
$W_i$
of
![]() $W_i'$
with size
$W_i'$
with size
![]() $|W_1|$
. It is obvious that
$|W_1|$
. It is obvious that
![]() $W_1,\ldots ,W_k$
satisfy the condition.
$W_1,\ldots ,W_k$
satisfy the condition.
Applying Claim 6.3 with
![]() $H=K_k$
shows that we can find a
$H=K_k$
shows that we can find a
![]() $K_k[\delta n]$
such that the
$K_k[\delta n]$
such that the
![]() $i$
th-part is contained in
$i$
th-part is contained in
![]() $U_i$
, finishing the proof.
$U_i$
, finishing the proof.
6.2. Graphs with bounded VC-dimension
Given a set system
![]() $\mathcal{F}\subseteq 2^{X},$
a set
$\mathcal{F}\subseteq 2^{X},$
a set
![]() $S \subseteq X,$
is said to be shattered by
$S \subseteq X,$
is said to be shattered by
![]() $\mathcal{F}$
if for every
$\mathcal{F}$
if for every
![]() $B \subseteq S,$
there exists a set
$B \subseteq S,$
there exists a set
![]() $F \in \mathcal{F}$
such that
$F \in \mathcal{F}$
such that
![]() $F \cap S = B.$
The VC-dimension of
$F \cap S = B.$
The VC-dimension of
![]() $\mathcal{F}$
is the size of the largest set shattered by
$\mathcal{F}$
is the size of the largest set shattered by
![]() $\mathcal{F}.$
Given a graph
$\mathcal{F}.$
Given a graph
![]() $G=(V,E)$
, for any vertex
$G=(V,E)$
, for any vertex
![]() $v\in V$
, let
$v\in V$
, let
![]() $N_{G}(v)$
be the set of its neighbours. The VC-dimension of
$N_{G}(v)$
be the set of its neighbours. The VC-dimension of
![]() $G$
is defined to be the VC-dimension of the set system
$G$
is defined to be the VC-dimension of the set system
![]() $\{N_{G}(v)\subseteq V(G)\,:\,v\in V(G)\}.$
$\{N_{G}(v)\subseteq V(G)\,:\,v\in V(G)\}.$
We start with a simple proposition about graphs with VC-dimension
![]() $1$
.
$1$
.
Proposition 6.4.
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with VC-dimension
$n$
-vertex graph with VC-dimension
![]() $1$
, then the following holds.
$1$
, then the following holds.
-
(1) If
 $G$
contains a copy of a triangle with vertices
$G$
contains a copy of a triangle with vertices
 $x_{1},x_{2},x_{3}$
, then any vertex
$x_{1},x_{2},x_{3}$
, then any vertex
 $v\in V(G){\setminus} \{x_{1},x_{2},x_{3}\}$
is adjacent to at least
$v\in V(G){\setminus} \{x_{1},x_{2},x_{3}\}$
is adjacent to at least
 $2$
vertices of
$2$
vertices of
 $x_{1},x_{2},x_{3}$
.
$x_{1},x_{2},x_{3}$
. -
(2) If there is a copy of
 $P_{5}\,:\!=\, y_{1}y_{2}y_{3}y_{4}y_{5}$
, then at least one of the pairs
$P_{5}\,:\!=\, y_{1}y_{2}y_{3}y_{4}y_{5}$
, then at least one of the pairs
 $y_{1}y_{4},y_{2}y_{4},y_{2}y_{5}$
is adjacent.
$y_{1}y_{4},y_{2}y_{4},y_{2}y_{5}$
is adjacent.
Proof. To see (1), if a vertex
![]() $v\in V(G){\setminus} \{x_{1},x_{2},x_{3}\}$
is not adjacent to two vertices, say
$v\in V(G){\setminus} \{x_{1},x_{2},x_{3}\}$
is not adjacent to two vertices, say
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, then the set
$x_2$
, then the set
![]() $\{x_1, x_2\}$
is shattered. To see (2), note that if none of the edges
$\{x_1, x_2\}$
is shattered. To see (2), note that if none of the edges
![]() $y_{1}y_{4},y_{2}y_{4},y_{2}y_{5}$
are present, then the set
$y_{1}y_{4},y_{2}y_{4},y_{2}y_{5}$
are present, then the set
![]() $\{y_2, y_4\}$
is shattered.
$\{y_2, y_4\}$
is shattered.
We need the following regularity lemma for graphs of bounded VC-dimension.
Theorem 6.5 [Reference Fox, Pach and Suk15]. Let
![]() $\gamma \in (0,{1 \over 4})$
and
$\gamma \in (0,{1 \over 4})$
and
![]() $G=(V,E)$
be an
$G=(V,E)$
be an
![]() $n$
-vertex graph with VC-dimension
$n$
-vertex graph with VC-dimension
![]() $d$
. Then
$d$
. Then
![]() $V(G)$
has an equitable partition
$V(G)$
has an equitable partition
![]() $V(G)=V_{1}\cup \cdots \cup V_{K}$
with
$V(G)=V_{1}\cup \cdots \cup V_{K}$
with
![]() ${8 \over \gamma }\leqslant K\leqslant c{({1 \over \gamma })^{2d + 1}}$
parts such that all but a
${8 \over \gamma }\leqslant K\leqslant c{({1 \over \gamma })^{2d + 1}}$
parts such that all but a
![]() $\gamma$
-fraction of the pairs of parts are
$\gamma$
-fraction of the pairs of parts are
![]() $\gamma$
-homogeneous, where
$\gamma$
-homogeneous, where
![]() $c=c(d)$
is a constant depending only on
$c=c(d)$
is a constant depending only on
![]() $d$
.
$d$
.
Proof of Theorem
1.10. We first argue that there are graphs with VC-dimension 2 but have no
![]() $B_2$
property. Let
$B_2$
property. Let
![]() $H_0$
be the point–line incidence bipartite graph of the projective plane
$H_0$
be the point–line incidence bipartite graph of the projective plane
![]() $\mathrm{PG}(2,q)$
. Then
$\mathrm{PG}(2,q)$
. Then
![]() $H_0$
is balanced bipartite with
$H_0$
is balanced bipartite with
![]() $|A|=|B|=q^2+q+1$
, is
$|A|=|B|=q^2+q+1$
, is
![]() $(q+1)$
-regular, and
$(q+1)$
-regular, and
![]() $C_4$
-free. Write
$C_4$
-free. Write
![]() $n\,:\!=\,|A|+|B|=2(q^2+q+1)$
. Obtain
$n\,:\!=\,|A|+|B|=2(q^2+q+1)$
. Obtain
![]() $H$
by keeping each edge of
$H$
by keeping each edge of
![]() $H_0$
independently with probability
$H_0$
independently with probability
![]() $p=c\,q^{-1/3}$
(fixed
$p=c\,q^{-1/3}$
(fixed
![]() $c\gt 0$
). Since
$c\gt 0$
). Since
![]() $H\subseteq H_0$
, the graph
$H\subseteq H_0$
, the graph
![]() $H$
is
$H$
is
![]() $C_4$
-free and, by Chernoff bounds,
$C_4$
-free and, by Chernoff bounds,
In any
![]() $C_4$
-free graph a
$C_4$
-free graph a
![]() $3$
-set cannot be shattered, because shattering
$3$
-set cannot be shattered, because shattering
![]() $Y$
forces two vertices to share two neighbours from
$Y$
forces two vertices to share two neighbours from
![]() $Y$
, creating a
$Y$
, creating a
![]() $C_4$
. Thus
$C_4$
. Thus
![]() $H$
has VC-dimension at most 2.
$H$
has VC-dimension at most 2.
Finally, let
![]() $\overline H$
be the bipartite complement in
$\overline H$
be the bipartite complement in
![]() $K_{A,B}$
. For fixed
$K_{A,B}$
. For fixed
![]() $A'\subseteq A$
and
$A'\subseteq A$
and
![]() $B'\subseteq B$
with
$B'\subseteq B$
with
![]() $|A'|=|B'|=t$
,
$|A'|=|B'|=t$
,
Therefore, by the first-moment method,
for any fixed
![]() $\varepsilon \gt 0$
when
$\varepsilon \gt 0$
when
![]() $t\geqslant n^{2/3+\varepsilon }$
. Consequently, w.h.p.
$t\geqslant n^{2/3+\varepsilon }$
. Consequently, w.h.p.
![]() $\overline H$
contains no
$\overline H$
contains no
![]() $K_{t,t}$
of size
$K_{t,t}$
of size
![]() $n^{2/3+o(1)}$
, and we obtain graphs of VC-dimension at most
$n^{2/3+o(1)}$
, and we obtain graphs of VC-dimension at most
![]() $2$
without the
$2$
without the
![]() $B_2$
property.
$B_2$
property.
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with VC-dimension
$n$
-vertex graph with VC-dimension
![]() $1$
and
$1$
and
![]() $e(G)=c\binom{n}{2}$
with
$e(G)=c\binom{n}{2}$
with
![]() $c\gt 0$
. It is left to prove that
$c\gt 0$
. It is left to prove that
![]() $G$
contains a
$G$
contains a
![]() $K_2[t]$
with
$K_2[t]$
with
![]() $t=\Omega _c(n)$
. We consider two cases.
$t=\Omega _c(n)$
. We consider two cases.
Case 1.
![]() $c\geqslant {{99} \over {100}}.$
$c\geqslant {{99} \over {100}}.$
Claim 6.6.
![]() $G$
contains a subgraph
$G$
contains a subgraph
![]() $G'$
with
$G'$
with
![]() $|G'|\geqslant {{9n} \over {10}}$
and
$|G'|\geqslant {{9n} \over {10}}$
and
![]() $\delta (G')\geqslant {{2n} \over 3}$
.
$\delta (G')\geqslant {{2n} \over 3}$
.
Proof of claim. We iteratively define a sequence of graphs
![]() $G_{0}=G\supseteq G_{1}\supseteq G_{2}\supseteq \cdots$
, where for each
$G_{0}=G\supseteq G_{1}\supseteq G_{2}\supseteq \cdots$
, where for each
![]() $i\geqslant 1$
, we obtain
$i\geqslant 1$
, we obtain
![]() $G_{i}$
by removing one vertex with degree less than
$G_{i}$
by removing one vertex with degree less than
![]() ${{2n} \over 3}$
from
${{2n} \over 3}$
from
![]() $G_{i-1}$
if it exists, otherwise we stop. Note that the number of non-adjacent pair of vertices in
$G_{i-1}$
if it exists, otherwise we stop. Note that the number of non-adjacent pair of vertices in
![]() $G$
is at most
$G$
is at most
![]() ${1 \over {100}}\left( \frac{n}{2} \right)$
and each removal decreases the number of non-edges by at least
${1 \over {100}}\left( \frac{n}{2} \right)$
and each removal decreases the number of non-edges by at least
![]() ${n \over 3}.$
Hence, the process will stop after fewer than
${n \over 3}.$
Hence, the process will stop after fewer than
![]() ${3 \over {100}}n$
steps. Let
${3 \over {100}}n$
steps. Let
![]() $G'$
be the resulting subgraph. It follows that
$G'$
be the resulting subgraph. It follows that
![]() $\delta (G')\geqslant {{2n} \over 3}$
and
$\delta (G')\geqslant {{2n} \over 3}$
and
![]() $|V(G')|\geqslant {9 \over {10}}n$
.
$|V(G')|\geqslant {9 \over {10}}n$
.
The following claim implies that the graph
![]() $G'$
is a complete multipartite graph.
$G'$
is a complete multipartite graph.
Claim 6.7.
For any pair of non-adjacent vertices
![]() $u,v\in V(G')$
,
$u,v\in V(G')$
,
![]() $N_{G'}(u)=N_{G'}(v)$
.
$N_{G'}(u)=N_{G'}(v)$
.
Proof of claim. Let
![]() $u,v\in V(G')$
be a pair of vertices such that
$u,v\in V(G')$
be a pair of vertices such that
![]() $uv\notin E(G')$
. Suppose that there exists a vertex
$uv\notin E(G')$
. Suppose that there exists a vertex
![]() $w$
such that
$w$
such that
![]() $uw\in E(G')$
and
$uw\in E(G')$
and
![]() $vw\notin E(G')$
, note that
$vw\notin E(G')$
, note that
![]() $u$
and
$u$
and
![]() $w$
have a common neighbour
$w$
have a common neighbour
![]() $z\in V(G')$
as
$z\in V(G')$
as
![]() $\delta (G')\geqslant {{2n} \over 3}$
. That means
$\delta (G')\geqslant {{2n} \over 3}$
. That means
![]() $v$
can be adjacent to at most one vertex of the triangle
$v$
can be adjacent to at most one vertex of the triangle
![]() $uwz$
, a contradiction to Proposition 6.4.
$uwz$
, a contradiction to Proposition 6.4.
Since
![]() $G'$
is a complete multipartite graph and
$G'$
is a complete multipartite graph and
![]() $\delta (G')\geqslant {{2n} \over 3},$
it follows that each of the parts has size at most
$\delta (G')\geqslant {{2n} \over 3},$
it follows that each of the parts has size at most
![]() ${n \over 3}.$
Since
${n \over 3}.$
Since
![]() $|V(G')|\geqslant {{9n} \over {10}},$
the parts of
$|V(G')|\geqslant {{9n} \over {10}},$
the parts of
![]() $G'$
can be split into two sides such that each of the sides has size at least
$G'$
can be split into two sides such that each of the sides has size at least
![]() ${n \over 5},$
implying that
${n \over 5},$
implying that
![]() $G$
contains
$G$
contains
![]() ${K_2}[{n \over 5}]$
as desired.
${K_2}[{n \over 5}]$
as desired.
Case 2.
![]() $c\lt {{99} \over {100}}$
.
$c\lt {{99} \over {100}}$
.
Let
![]() $\gamma =10^{-5}c$
. By Theorem 6.5, we can partition
$\gamma =10^{-5}c$
. By Theorem 6.5, we can partition
![]() $V(G)$
into
$V(G)$
into
![]() $V_{1}\cup V_{2}\cup \cdots \cup V_{K}$
with
$V_{1}\cup V_{2}\cup \cdots \cup V_{K}$
with
![]() $K\leqslant c'{({1 \over \gamma })^3}$
for some
$K\leqslant c'{({1 \over \gamma })^3}$
for some
![]() $c'\gt 0$
, such that all but a
$c'\gt 0$
, such that all but a
![]() $\gamma$
-fraction of the pairs of parts are
$\gamma$
-fraction of the pairs of parts are
![]() $\gamma$
-homogeneous. Since
$\gamma$
-homogeneous. Since
![]() $c\binom{n}{2}\leqslant e(G) \leqslant {\frac{99}{100}}\binom{n}{2},$
it is easy to see that there are three parts
$c\binom{n}{2}\leqslant e(G) \leqslant {\frac{99}{100}}\binom{n}{2},$
it is easy to see that there are three parts
![]() $V_{i},V_{j},V_{k}$
such that
$V_{i},V_{j},V_{k}$
such that
![]() $(V_{i},V_{j})$
is
$(V_{i},V_{j})$
is
![]() $\gamma$
-dense,
$\gamma$
-dense,
![]() $(V_{j},V_{k})$
is
$(V_{j},V_{k})$
is
![]() $\gamma$
-sparse and
$\gamma$
-sparse and
![]() $|{V_i}| = |{V_j}| = |{V_k}| = m\geqslant {n \over {2K}}$
. Similarly as in Claim 6.6, we remove any vertex from
$|{V_i}| = |{V_j}| = |{V_k}| = m\geqslant {n \over {2K}}$
. Similarly as in Claim 6.6, we remove any vertex from
![]() $V_{j}$
with at most
$V_{j}$
with at most
![]() ${{4m} \over 5}$
neighbours in
${{4m} \over 5}$
neighbours in
![]() $V_i$
or at least
$V_i$
or at least
![]() ${m \over 5}$
neighbours in
${m \over 5}$
neighbours in
![]() $V_k.$
Let
$V_k.$
Let
![]() $U_j \subseteq V_j$
be the remaining set and observe that
$U_j \subseteq V_j$
be the remaining set and observe that
![]() $|U_j| \geqslant (1 - 10\gamma ) m$
and for every
$|U_j| \geqslant (1 - 10\gamma ) m$
and for every
![]() $u \in U_j,$
we have
$u \in U_j,$
we have
![]() ${d_{{V_i}}}(u)\geqslant {{4m} \over 5}$
and
${d_{{V_i}}}(u)\geqslant {{4m} \over 5}$
and
![]() ${d_{{V_k}}}(u)\leqslant {m \over 5}.$
${d_{{V_k}}}(u)\leqslant {m \over 5}.$
Note that there are at least
![]() ${{4m} \over 5}|{U_j}|{{3{m^2}} \over 4}$
edges between
${{4m} \over 5}|{U_j}|{{3{m^2}} \over 4}$
edges between
![]() $U_j$
and
$U_j$
and
![]() $V_i$
so we can pick a vertex
$V_i$
so we can pick a vertex
![]() $v \in V_i$
with
$v \in V_i$
with
![]() $|{N_{{U_j}}}(v)|\geqslant {{3m} \over 4}$
. We first claim that
$|{N_{{U_j}}}(v)|\geqslant {{3m} \over 4}$
. We first claim that
![]() $N_{U_{j}}(v)$
is an independent set. Indeed, if there is an edge
$N_{U_{j}}(v)$
is an independent set. Indeed, if there is an edge
![]() $u_{1}u_{2}$
in
$u_{1}u_{2}$
in
![]() $N_{U_j}(v)$
, then every vertex in
$N_{U_j}(v)$
, then every vertex in
![]() $V_{k}$
should be adjacent to at least one of
$V_{k}$
should be adjacent to at least one of
![]() $u_{1},u_{2}$
by Proposition 6.4 (1). However, then one of
$u_{1},u_{2}$
by Proposition 6.4 (1). However, then one of
![]() $u_1, u_2$
has at least
$u_1, u_2$
has at least
![]() ${m \over 2}$
neighbours in
${m \over 2}$
neighbours in
![]() $V_k,$
a contradiction.
$V_k,$
a contradiction.
Moreover, we have the following claim.
Claim 6.8.
For any distinct vertices
![]() $u_{1},u_{2}\in N_{U_{j}}(v)$
, either
$u_{1},u_{2}\in N_{U_{j}}(v)$
, either
![]() $N_{V_{i}}(u_{1})\subseteq N_{V_{i}}(u_{2})$
, or
$N_{V_{i}}(u_{1})\subseteq N_{V_{i}}(u_{2})$
, or
![]() $N_{V_{i}}(u_{2})\subseteq N_{V_{i}}(u_{1})$
.
$N_{V_{i}}(u_{2})\subseteq N_{V_{i}}(u_{1})$
.
Proof of claim. Suppose this is not the case so there is a vertex
![]() $v_{1}\in N_{V_{i}}(u_{1}){\setminus} N_{V_{i}}(u_{2})$
and a vertex
$v_{1}\in N_{V_{i}}(u_{1}){\setminus} N_{V_{i}}(u_{2})$
and a vertex
![]() $v_{2}\in N_{V_{i}}(u_{2}){\setminus} N_{V_{i}}(u_{1})$
. Then
$v_{2}\in N_{V_{i}}(u_{2}){\setminus} N_{V_{i}}(u_{1})$
. Then
![]() $v_{1}u_{1}vu_{2}v_{2}$
forms a copy of
$v_{1}u_{1}vu_{2}v_{2}$
forms a copy of
![]() $P_{5}$
. However, none of the edges
$P_{5}$
. However, none of the edges
![]() $v_{1}u_{2},u_{1}u_{2},u_{1}v_{2}$
are present, contradicting Proposition 6.4 (2).
$v_{1}u_{2},u_{1}u_{2},u_{1}v_{2}$
are present, contradicting Proposition 6.4 (2).
Now, consider a vertex
![]() $u \in N_{U_{j}}(v)$
minimising
$u \in N_{U_{j}}(v)$
minimising
![]() $|N_{V_i}(u)|$
. Then, for any
$|N_{V_i}(u)|$
. Then, for any
![]() $u' \in N_{U_{j}}(v)$
, we have
$u' \in N_{U_{j}}(v)$
, we have
![]() $N_{V_i}(u') \supseteq N_{V_i}(u)$
implying the existence of
$N_{V_i}(u') \supseteq N_{V_i}(u)$
implying the existence of
![]() ${K_2}[{{3m} \over 4}]$
in
${K_2}[{{3m} \over 4}]$
in
![]() $G$
.
$G$
.
This completes the proof of Theorem 1.10.
7. Concluding remarks
Recall that
![]() $g(k)$
is the minimum
$g(k)$
is the minimum
![]() $r\in \mathbb{N}$
such that if any
$r\in \mathbb{N}$
such that if any
![]() $n$
-vertex ordered graph
$n$
-vertex ordered graph
![]() $G$
with no induced monotone
$G$
with no induced monotone
![]() $P_{2k}$
satisfies
$P_{2k}$
satisfies
![]() $\varrho _r(\overline {G})\gt 0$
, then
$\varrho _r(\overline {G})\gt 0$
, then
![]() $\overline {G}$
contains a copy of
$\overline {G}$
contains a copy of
![]() ${K_2}[\Omega ({n \over {\log n}})]$
. We determined
${K_2}[\Omega ({n \over {\log n}})]$
. We determined
![]() $g(k)$
up to a factor of
$g(k)$
up to a factor of
![]() $2$
. It would be interesting to close this gap. To this end, we make the following conjecture on the Ramsey problem for
$2$
. It would be interesting to close this gap. To this end, we make the following conjecture on the Ramsey problem for
![]() $f(k)$
defined in Definition 3.1.
$f(k)$
defined in Definition 3.1.
Conjecture C.
![]() $f(k) = \lfloor {{{{k^2}} \over 4}} \rfloor + 1$
.
$f(k) = \lfloor {{{{k^2}} \over 4}} \rfloor + 1$
.
By our construction in Section 4, the conjecture above, if true, would be optimal, implying that
![]() $g(k) = f(k) = \lfloor {{{{k^2}} \over 4}} \rfloor + 1$
. With the assistance of computers, we checked that Conjecture C is true for
$g(k) = f(k) = \lfloor {{{{k^2}} \over 4}} \rfloor + 1$
. With the assistance of computers, we checked that Conjecture C is true for
![]() $k\leqslant 6$
.
$k\leqslant 6$
.
An important theme we systematically investigate in this paper is that of ‘replacing edge density by clique density’. We believe that this theme merits further study. A recent result of Holmsen [Reference Holmsen21] is of this flavour. It is known that for any intersection graph
![]() $G$
of axis-aligned boxes in
$G$
of axis-aligned boxes in
![]() $\mathbb{R}^d$
, if
$\mathbb{R}^d$
, if
![]() $G$
has edge density larger than
$G$
has edge density larger than
![]() $1 - {1 \over d}$
, then it contains a linear-size clique. A corollary of Holmsen’s result shows that it suffices to require positive
$1 - {1 \over d}$
, then it contains a linear-size clique. A corollary of Holmsen’s result shows that it suffices to require positive
![]() $K_{d+1}$
-density.
$K_{d+1}$
-density.
Tomon [Reference Tomon34] proved that if
![]() $G$
is the complement of a string graph and has edge density larger than
$G$
is the complement of a string graph and has edge density larger than
![]() ${3 \over 4}$
, then
${3 \over 4}$
, then
![]() $G$
contains a linear-size biclique. Following our theme here, we propose the following conjecture.
$G$
contains a linear-size biclique. Following our theme here, we propose the following conjecture.
Conjecture D.
Let
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $G$
be the complement of a string graph. If
$G$
be the complement of a string graph. If
![]() $\varrho _{4s+1}(G)\gt 0$
, then
$\varrho _{4s+1}(G)\gt 0$
, then
![]() $G$
contains a
$G$
contains a
![]() $K_{s+1}[\delta n]$
, where
$K_{s+1}[\delta n]$
, where
![]() $\delta =\delta (\varepsilon )\gt 0$
.
$\delta =\delta (\varepsilon )\gt 0$
.
We remark that taking disjoint union of tight examples in [Reference Tomon34] shows that if the conjecture is true, it is optimal in the sense that positive
![]() $K_{4s}$
-density does not suffices to guarantee linear-size blowup of
$K_{4s}$
-density does not suffices to guarantee linear-size blowup of
![]() $K_{s+1}$
.
$K_{s+1}$
.
In Theorem 1.10, we show that linear-size biclique is guaranteed only in dense graphs with VC-dimension 1. How large a biclique do dense graphs with larger VC-dimension contain? Anthony, Brightwell and Cooper [Reference Anthony, Brightwell and Cooper1] proved that the random graph
![]() $G(n, p)$
with edge probability
$G(n, p)$
with edge probability
![]() $p = 1 - {n^{ - {1 \over d} + O({1 \over {{d^2}}})}}$
, with high probability, has VC-dimension at most
$p = 1 - {n^{ - {1 \over d} + O({1 \over {{d^2}}})}}$
, with high probability, has VC-dimension at most
![]() $d$
and is
$d$
and is
![]() $K_2[t]$
-free, where
$K_2[t]$
-free, where
![]() $t = {n^{{1 \over d} + O({1 \over {{d^2}}})}}$
. Hence, there exist graphs with
$t = {n^{{1 \over d} + O({1 \over {{d^2}}})}}$
. Hence, there exist graphs with
![]() $(1 - o(1)) \binom {n}{2}$
edges, VC-dimension at most
$(1 - o(1)) \binom {n}{2}$
edges, VC-dimension at most
![]() $d$
and no biclique of size
$d$
and no biclique of size
![]() ${n^{{1 \over d} + O({1 \over {{d^2}}})}}$
. On the other hand, we can show that any dense graph with VC-dimension
${n^{{1 \over d} + O({1 \over {{d^2}}})}}$
. On the other hand, we can show that any dense graph with VC-dimension
![]() $d$
contains a biclique of size
$d$
contains a biclique of size
![]() $\Omega ({n^{{1 \over {d + 1}}}})$
.
$\Omega ({n^{{1 \over {d + 1}}}})$
.
Proposition 7.1.
Let
![]() $d\geqslant 2$
be positive integers and
$d\geqslant 2$
be positive integers and
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with VC-dimension
$n$
-vertex graph with VC-dimension
![]() $d$
. If
$d$
. If
![]() $e(G)\geqslant c\binom{n}{2}$
for some
$e(G)\geqslant c\binom{n}{2}$
for some
![]() $c\gt 0$
, then
$c\gt 0$
, then
![]() $G$
contains a copy of
$G$
contains a copy of
![]() ${K_2}[c'{n^{{1 \over {d + 1}}}}]$
for some
${K_2}[c'{n^{{1 \over {d + 1}}}}]$
for some
![]() $c'$
.
$c'$
.
A system
![]() $\mathcal{X}\subseteq 2^V$
is
$\mathcal{X}\subseteq 2^V$
is
![]() $s$
-separated if for any
$s$
-separated if for any
![]() $F,F'\in \mathcal{X}$
,
$F,F'\in \mathcal{X}$
,
![]() $|F\triangle F'|\geqslant s$
.
$|F\triangle F'|\geqslant s$
.
Lemma 7.2 (Haussler [Reference Haussler20]). Let
![]() $\mathcal{F}\subseteq 2^{V}$
be a set system such that
$\mathcal{F}\subseteq 2^{V}$
be a set system such that
![]() $\mathcal{F}$
has VC-dimension
$\mathcal{F}$
has VC-dimension
![]() $d$
. If
$d$
. If
![]() $\mathcal{X}\subseteq \mathcal{F}$
is
$\mathcal{X}\subseteq \mathcal{F}$
is
![]() $s$
-separated, then
$s$
-separated, then
![]() $|\mathcal{X}|\leqslant c_{1} (\frac{|V|}{s})^{d}$
, where
$|\mathcal{X}|\leqslant c_{1} (\frac{|V|}{s})^{d}$
, where
![]() $c_{1}=c_{1}(d)$
.
$c_{1}=c_{1}(d)$
.
Proof of Proposition
7.1. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with VC-dimension
$n$
-vertex graph with VC-dimension
![]() $d$
and
$d$
and
![]() $e(G)\geqslant c\binom{n}{2}$
. Deleting low degree vertices, we get from
$e(G)\geqslant c\binom{n}{2}$
. Deleting low degree vertices, we get from
![]() $G$
a subgraph
$G$
a subgraph
![]() $G'$
with
$G'$
with
![]() $\delta (G')\geqslant cn/2$
. Let
$\delta (G')\geqslant cn/2$
. Let
![]() $\mathcal{F}'\,:\!=\,\{N_{G'}(v)\subseteq V(G')\,:\, v\in V(G')\}$
, the VC-dimension of
$\mathcal{F}'\,:\!=\,\{N_{G'}(v)\subseteq V(G')\,:\, v\in V(G')\}$
, the VC-dimension of
![]() $\mathcal{F}'$
is also at most
$\mathcal{F}'$
is also at most
![]() $d$
.
$d$
.
Set
![]() $s = |G'{|^{1 - {1 \over {d + 1}}}}$
and take a maximal
$s = |G'{|^{1 - {1 \over {d + 1}}}}$
and take a maximal
![]() $s$
-separated subfamily
$s$
-separated subfamily
![]() $\mathcal{X}=\{N_{G'}(v_{1}),N_{G'}(v_{2}),\ldots ,$
$\mathcal{X}=\{N_{G'}(v_{1}),N_{G'}(v_{2}),\ldots ,$
![]() $N_{G'}(v_{m})\}\subseteq \mathcal{F}'$
. We have
$N_{G'}(v_{m})\}\subseteq \mathcal{F}'$
. We have
![]() $m\leqslant {c_1}{({{|G'|} \over s})^d}$
by Lemma 7.2. Then, partition
$m\leqslant {c_1}{({{|G'|} \over s})^d}$
by Lemma 7.2. Then, partition
![]() $V(G')$
into
$V(G')$
into
![]() $V_{1}\sqcup V_{2}\sqcup \cdots \sqcup V_{m}$
with
$V_{1}\sqcup V_{2}\sqcup \cdots \sqcup V_{m}$
with
![]() $v_{i}\in V_{i}$
as follows. We put
$v_{i}\in V_{i}$
as follows. We put
![]() $N_{G'}(v)\in \mathcal{F'}{\setminus} \mathcal{X}$
into
$N_{G'}(v)\in \mathcal{F'}{\setminus} \mathcal{X}$
into
![]() $V_{i}$
if
$V_{i}$
if
![]() $i$
is the smallest index such that
$i$
is the smallest index such that
![]() $|N_{G'}(v)\triangle N_{G'}(v_{i})|\leqslant s$
. Note that after partitioning, each set in
$|N_{G'}(v)\triangle N_{G'}(v_{i})|\leqslant s$
. Note that after partitioning, each set in
![]() $\mathcal{F'}{\setminus} \mathcal{X}$
belongs to some part
$\mathcal{F'}{\setminus} \mathcal{X}$
belongs to some part
![]() $V_{i}$
. Moreover, every pair of vertices
$V_{i}$
. Moreover, every pair of vertices
![]() $u,v$
with their neighbourhoods in the same part satisfies
$u,v$
with their neighbourhoods in the same part satisfies
![]() $|N_{G'}(u)\triangle N_{G'}(v)|\leqslant 2s$
by the triangle inequality.
$|N_{G'}(u)\triangle N_{G'}(v)|\leqslant 2s$
by the triangle inequality.
Now pick arbitrary vertices
![]() $v_{1},v_{2},\ldots ,v_{q}$
from some part
$v_{1},v_{2},\ldots ,v_{q}$
from some part
![]() $V_{i}$
with
$V_{i}$
with
![]() $|{V_i}| = \Omega ({n \over m})$
, where
$|{V_i}| = \Omega ({n \over m})$
, where
![]() $q = \Omega ({n^{{1 \over {d + 1}}}})$
. As
$q = \Omega ({n^{{1 \over {d + 1}}}})$
. As
![]() $\delta (G')\gt (2q+1)s+q$
, we see that
$\delta (G')\gt (2q+1)s+q$
, we see that
![]() $\big |\bigcap _{h\in [q]}N_{G'}(v_{h})\big |\geqslant |N_{G'}(v_{1})|-(2q+1)s\geqslant q$
. Note that
$\big |\bigcap _{h\in [q]}N_{G'}(v_{h})\big |\geqslant |N_{G'}(v_{1})|-(2q+1)s\geqslant q$
. Note that
![]() $|{V_i}|\Omega ({n^{1 - {1 \over {d + 1}}}})\gt q$
, thus there is a biclique of size
$|{V_i}|\Omega ({n^{1 - {1 \over {d + 1}}}})\gt q$
, thus there is a biclique of size
![]() $q$
.
$q$
.
Funding statement
Hong Liu, Zixiang Xu: supported by IBS-R029-C4. Zhuo Wu: Z. Wu acknowledge the bilateral AEI+DFG research project PCI2024-155080-2: SRC-ExCo-Structure, Randomness and Computational Methods in Extremal Combinatorics, and the PID2023-147202NB-I00. COCOA: COntemporary COmbinatorics and its Applications, all of them funded by MICIU/AEI/10.13039/501100011033.