Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-29T15:54:03.475Z Has data issue: false hasContentIssue false
  • English
  • Français

The Dual BKR Inequality and Rudich's Conjecture

Published online by Cambridge University Press:  02 December 2010

JEFF KAHN ,
MICHAEL SAKS  and
CLIFFORD SMYTH
JEFF KAHN
Affiliation:
Mathematics Department, Rutgers University, Piscataway, NJ, USA (e-mail: jkahn@math.rutgers.edu, saks@math.rutgers.edu)
MICHAEL SAKS
Affiliation:
Mathematics Department, Rutgers University, Piscataway, NJ, USA (e-mail: jkahn@math.rutgers.edu, saks@math.rutgers.edu)
CLIFFORD SMYTH
Affiliation:
Mathematics Department, University of North Carolina Greensboro, Greensboro, NC, USA (e-mail: cdsmyth@uncg.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 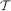be a set of terms over an arbitrary (but finite) number of Boolean variables. Let U(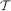) be the set of truth assignments that satisfy exactly one term in 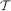. Motivated by questions in computational complexity, Rudich conjectured that there exist ∊, δ > 0 such that, if 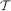is any set of terms for which U(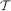) contains at least a (1−∊)-fraction of all truth assignments, then there exists a term t ∈ 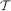such that at least a δ-fraction of assignments satisfy some term of 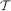sharing a variable with t [8].

We prove a stronger version: for any independent assignment of the variables (not necessarily the uniform one), if the measure of U(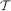) is at least 1 − ∊, there exists a t ∈ 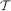such that the measure of the set of assignments satisfying either t or some term incompatible with t (i.e., having no satisfying assignments in common with t) is at least 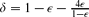. (A key part of the proof is a correlation-like inequality on events in a finite product probability space that is in some sense dual to Reimer's inequality [11], a.k.a. the BKR inequality [5], or the van den Berg–Kesten conjecture [3].)

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 20 , Issue 2 , March 2011 , pp. 257 - 266
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, third edition, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley.CrossRefGoogle Scholar
[2]van den Berg, J. and Fiebig, U. (1987) On a combinatorial conjecture concerning disjoint occurrences of events. Ann. Probab. 15 354–374.Google Scholar
[3]van den Berg, J. and Kesten, H. (1985) Inequalities with applications to percolation and reliability. J. Appl. Probab. 22 556–569.CrossRefGoogle Scholar
[4]Erdős, P. and Lovász, L. (1975) Problems and results on 3-chromatic hypergraphs and some related questions. In Infinite and Finite Sets: Colloq., Keszthely, 1973; Dedicated to P. Erdős on his 60th Birthday, Vol. II, János Bolyai, Vol.10, North-Holland, pp. 609–627.Google Scholar
[5]Goldstein, L. and Rinott, Y. (2007) Functional BKR inequalities, and their duals, with applications. J. Theoret. Probab. 20 275–293.CrossRefGoogle Scholar
[6]Harris, T. E. (1960) A lower bound for the critical probability in a certain percolation process. Proc. Cambridge Philos. Soc. 56 13–20.CrossRefGoogle Scholar
[7]Impagliazzo, R. and Rudich, S. Personal communication.Google Scholar
[8]Impagliazzo, R. and Rudich, S. (1990) Limits on the provable consequences of one-way permutations. In Advances in Cryptology: CRYPTO '88 (Santa Barbara), Vol. 403 of Lecture Notes in Computer Science, Springer, pp. 8–26.CrossRefGoogle Scholar
[9]Kahn, J., Saks, M. and Smyth, C. (2000) A dual version of Reimer's inequality and a proof of Rudich's conjecture. In 15th Annual IEEE Conference on Computational Complexity (Florence), IEEE Computer Society, pp. 98–103.Google Scholar
[10]Kleitman, D. J. (1966) Families of non-disjoint subsets. J. Combin. Theory 1 153–155.CrossRefGoogle Scholar
[11]Reimer, D. (2000) Proof of the van den Berg–Kesten conjecture. Combin. Probab. Comput. 9 27–32.CrossRefGoogle Scholar
[12]Rudich, S. (ca. 1990) Unpublished.Google Scholar
[13]Smyth, C. (2002) Reimer's inequality and Tardos' conjecture. In Proc. 34th Annual ACM Symposium on Theory of Computing (New York), ACM, pp. 218–221.Google Scholar
[14]Szegedy, M. (ca. 1990) Unpublished.Google Scholar
[15]Tardos, G. (1989) Query complexity, or why is it difficult to separate NPA ∩ co-NPA from PA by random oracles A? Combinatorica 9 385–392.CrossRefGoogle Scholar
[16]Tardos, G. (ca. 1990) Unpublished.Google Scholar