Hostname: page-component-77c78cf97d-v4t4b Total loading time: 0 Render date: 2026-04-25T19:57:28.135Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluctuations of subgraph counts in graphon based random graphs

Part of: Limit theorems Graph theory

Published online by Cambridge University Press:  09 December 2022

Bhaswar B. Bhattacharya ,
Anirban Chatterjee  and
Svante Janson Open the ORCID record for Svante Janson [Opens in a new window]
Bhaswar B. Bhattacharya*
Affiliation:
Department of Statistics and Data Science, University of Pennsylvania, Philadelphia, PA 19104, USA
Anirban Chatterjee
Affiliation:
Department of Statistics and Data Science, University of Pennsylvania, Philadelphia, PA 19104, USA
Svante Janson
Affiliation:
Department of Mathematics, Uppsala University, PO Box 480, SE-751 06 Uppsala, Sweden
*
*Corresponding author. Email: bhaswar@wharton.upenn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a graphon 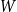$W$ and a finite simple graph 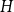$H$, with vertex set 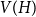$V(H)$, denote by 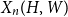$X_n(H, W)$ the number of copies of 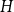$H$ in a 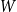$W$-random graph on $n$ vertices. The asymptotic distribution of 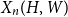$X_n(H, W)$ was recently obtained by Hladký, Pelekis, and Šileikis [17] in the case where 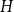$H$ is a clique. In this paper, we extend this result to any fixed graph 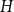$H$. Towards this we introduce a notion of 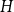$H$-regularity of graphons and show that if the graphon 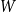$W$ is not 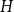$H$-regular, then 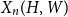$X_n(H, W)$ has Gaussian fluctuations with scaling 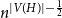$n^{|V(H)|-\frac{1}{2}}$. On the other hand, if 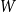$W$ is 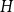$H$-regular, then the fluctuations are of order 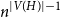$n^{|V(H)|-1}$ and the limiting distribution of 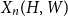$X_n(H, W)$ can have both Gaussian and non-Gaussian components, where the non-Gaussian component is a (possibly) infinite weighted sum of centred chi-squared random variables with the weights determined by the spectral properties of a graphon derived from 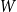$W$. Our proofs use the asymptotic theory of generalised 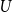$U$-statistics developed by Janson and Nowicki [22]. We also investigate the structure of 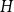$H$-regular graphons for which either the Gaussian or the non-Gaussian component of the limiting distribution (but not both) is degenerate. Interestingly, there are also 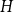$H$-regular graphons 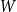$W$ for which both the Gaussian or the non-Gaussian components are degenerate, that is, 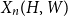$X_n(H, W)$ has a degenerate limit even under the scaling 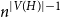$n^{|V(H)|-1}$. We give an example of this degeneracy with 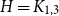$H=K_{1, 3}$ (the 3-star) and also establish non-degeneracy in a few examples. This naturally leads to interesting open questions on higher order degeneracies.

Keywords

Inhomogeneous random graphsgeneralised U-statisticsGraphonsLimit theoremsSubgraph counts

MSC classification

Primary: 05C80: Random graphs 60F05: Central limit and other weak theorems
Secondary: 05C60: Isomorphism problems (reconstruction conjecture, etc.) and homomorphisms (subgraph embedding, etc.)

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 3 , May 2023 , pp. 428 - 464
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

BBB partly supported by NSF CAREER Grant DMS-2046393 and a Sloan research fellowship. SJ partly supported by the Knut and Alice Wallenberg Foundation.

References

Austern, M. and Orbanz, P. (2022) Limit theorems for distributions invariant under groups of transformations. Ann. Stat. 50 1960–1991.CrossRefGoogle Scholar
Barbour, A. D., Karoński, M. and Ruciński, A. (1989) A central limit theorem for decomposable random variables with applications to random graphs. J. Comb. Theory, B 47 125–145.CrossRefGoogle Scholar
Basak, A. and Mukherjee, S. (2017) Universality of the mean-field for the Potts model. Probab. Theory Related Fields 168(3) 557–600.CrossRefGoogle Scholar
Bhattacharya, B. B. and Mukherjee, S. (2019) Monochromatic subgraphs in randomly colored graphons. Eur. J. Comb. 81 328–353.CrossRefGoogle Scholar
Bhattacharya, B. B., Diaconis, P. and Mukherjee, S. (2017) Universal limit theorems in graph coloring problems with connections to extremal combinatorics. Ann. Appl. Prob. 27 337–394.CrossRefGoogle Scholar
Bochner, S. (1933) Integration von Funktionen, deren Werte die Elemente eines Vektorraumes sind. Fund. Math. 20 262–176.CrossRefGoogle Scholar
Boguná, M. and Pastor-Satorras, R. (2003) Class of correlated random networks with hidden variables. Phys. Rev. E 68 036112.CrossRefGoogle ScholarPubMed
Bollobás, B., Janson, S. and Riordan, O. (2007) The phase transition in inhomogeneous random graphs. Random Struct. Algor. 31 3–122.CrossRefGoogle Scholar
Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T. and Vesztergombi, K. (2008) Convergent sequences of dense graphs I: Subgraph frequencies, metric properties and testing. Adv. Math. 219 1801–1851.CrossRefGoogle Scholar
Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T. and Vesztergombi, K. (2012) Convergent sequences of dense graphs II. Multiway cuts and statistical physics. Ann. Math. 176 151–219.CrossRefGoogle Scholar
Chatterjee, S. and Diaconis, P. (2013) Estimating and understanding exponential random graph models. Ann. Stat. 41 2428–2461.CrossRefGoogle Scholar
Chatterjee, S. and Varadhan, S. S. (2011) The large deviation principle for the Erdős-Rényi random graph. Eur. J. Comb. 32 1000–1017.CrossRefGoogle Scholar
Delmas, J.-F., Dhersin, J.-S. and Sciauveau, M. (2021) Asymptotic for the cumulative distribution function of the degrees and homomorphism densities for random graphs sampled from a graphon. Random Struct. Algor. 58(1) 94–149.CrossRefGoogle Scholar
Diaconis, P. and Freedman, D. (1981) On the statistics of vision: The Julesz conjecture. J. Math. Psychol. 24 112–138.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J. T. (1958) Linear Operators, Part I: General Theory. Wiley-Interscience.Google Scholar
Féray, V., Méliot, P.-L. and Nikeghbali, A. (2020) Graphons, permutons and the Thoma simplex: three mod-Gaussian moduli spaces. Proc. Lond. Math. Soc. 121 876–926.CrossRefGoogle Scholar
Hladký, J., Pelekis, C. and Šileikis, M. (2021) A limit theorem for small cliques in inhomogeneous random graphs. J. Graph Theory 97 578–599.CrossRefGoogle Scholar
Janson, S. (1990) A functional limit theorem for random graphs with applications to subgraph count statistics. Random Struct. Algor. 1(1) 15–37.CrossRefGoogle Scholar
Janson, S. (1994) Orthogonal decompositions and functional limit theorems for random graph statistics. Memoirs Amer. Math. Soc 111(534).CrossRefGoogle Scholar
Janson, S. (1997) Gaussian Hilbert Spaces. Cambridge University Press.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Rucinski, A. (2000) Random Graphs. John Wiley & Sons.CrossRefGoogle Scholar
Janson, S. and Nowicki, K. (1991) The asymptotic distributions of generalized $U$ -statistics with applications to random graphs. Probab Theory Rel 90(3) 341–375.CrossRefGoogle Scholar
Kallenberg, O. (2002) Foundations of Modern Probability. 2nd ed. Springer.CrossRefGoogle Scholar
Kaur, G. and Röllin, A. (2021) Higher-order fluctuations in dense random graph models. Electron J Probab 26 1–36.CrossRefGoogle Scholar
Lovász, L. (2012) Large Networks and Graph Limits. American Mathematical Soc.CrossRefGoogle Scholar
Lovász, L. and Szegedy, B. (2006) Limits of dense graph sequences. Journal of Combinatorial Theory, Series B 96(6) 933–957.CrossRefGoogle Scholar
Méliot, P. L. (2021) A central limit theorem for singular graphons. arXiv preprint arXiv:2103.15741.Google Scholar
Nowicki, K. (1989) Asymptotic normality of graph statistics. J Stat Plan Infer 21(2) 209–222.CrossRefGoogle Scholar
Nowicki, K. and Wierman, J. C. (1988) Subgraph counts in random graphs using incomplete $U$ -statistics methods. Discrete Math 72(1-3) 299–310.CrossRefGoogle Scholar
Ruciński, A. (1988) When are small subgraphs of a random graph normally distributed? Probab Theory Rel 78(1) 1–10.CrossRefGoogle Scholar
Zhang, Z.-S. (2022) Berry–Esseen bounds for generalized $U$ -statistics. Electron. J. Probab. 27 1–36.CrossRefGoogle Scholar